详解卷积神经网络反向传播
原文地址:http://jermmy.xyz/2017/12/16/2017-12-16-cnn-back-propagation/
在一般的全联接神经网络中,我们通过反向传播算法计算参数的导数。BP 算法本质上可以认为是链式法则在矩阵求导上的运用。但 CNN 中的卷积操作则不再是全联接的形式,因此 CNN 的 BP 算法需要在原始的算法上稍作修改。这篇文章主要讲一下 BP 算法在卷积层和 pooling 层上的应用。
原始的 BP 算法
首先,用两个例子回顾一下原始的 BP 算法。(不熟悉 BP 可以参考How the backpropagation algorithm works,不介意的话可以看我的读书笔记)
最简单的例子
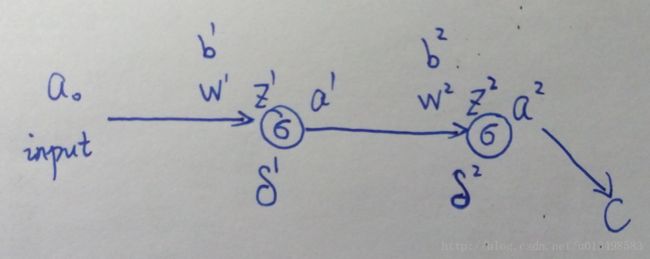
先看一个最简单的例子(偷个懒,搬个手绘图~囧~):
上图中,al 表示第 l 层的输出(a0 就是网络最开始的输入),网络的激活函数假设都是 σ(),wl 和 bl 表示第 l 层的参数,C表示 loss function,δl 表示第 l 层的误差,zl 是第 l 层神经元的输入,即 zl=wlal−1+bl,al=σ(zl)。
接下来要用 BP 算法求参数的导数 ∂C∂w 和 ∂C∂b。δ2=∂C∂z2=∂C∂a2∂a2∂z2=∂C∂a2σ′(z2)
δ1=∂C∂z1=δ2∂z2∂a1∂a1∂z1=δ2w2σ′(z1)
算出这两个误差项后,就可以直接求出导数了:∂C∂b2=∂C∂a2∂a2∂z2∂z2∂b2=δ2
∂C∂w2=∂C∂a2∂a2∂z2∂z2∂w2=δ2a1
∂C∂b1 和 ∂C∂w1 的求法是一样的,这里不在赘述。
次简单的例子
接下来稍微把网络变复杂一点:
符号的标记和上一个例子是一样的。要注意的是,这里的 Wl 不再是一个数,而变成一个权重矩阵,Wlkj 表示第 l−1 层的第 j 个神经元到第 l 层的第 k 个神经元的权值,如下图所示:
首先,还是要先求出网络的误差 δ。
δ21=∂C∂z21=∂C∂a21σ′(z21)δ22=∂C∂z22=∂C∂a22σ′(z22)
由此得到:δ2=[δ21δ22]=[∂C∂a21∂C∂a22]⊙[σ′(z21)σ′(z22)]⊙ 表示 elementwise 运算。
接着要根据 δ2 计算前一层的误差 δ1。δ11=∂C∂z11=∂C∂a21σ′(z21)∂z21∂a11∂a11∂z11+∂C∂a22σ′(z22)∂z22∂a11∂a11∂z11=∂C∂a21σ′(z21)W211σ′(z11)+∂C∂a22σ′(z22)W221σ′(z11)=[∂C∂a21σ′(z21)∂C∂a22σ′(z22)][W211W221]⊙[σ′(z11)]同理,δ12=[∂C∂a21σ′(z21)∂C∂a22σ′(z22)][W212W222]⊙[σ′(z12)]。
这样,我们就得到第 1 层的误差项:δ1=[W211W221W212W222][∂C∂z21∂C∂z22]⊙[σ′(z11)σ′(z12)]=W2Tδ2⊙σ′(z1)然后,根据误差项计算导数:∂C∂b2j=∂C∂z2j∂z2j∂b2j=δ2j∂C∂w2jk=∂C∂z2j∂z2j∂w2jk=a1kδ2j∂C∂b1j=∂C∂z1j∂z1j∂b1j=δ1j∂C∂w1jk=∂C∂z1j∂z1j∂w1jk=a0kδ1j
BP 算法的套路
在 BP 算法中,我们计算的误差项 δl 其实就是 loss function 对 zl 的导数 ∂C∂zl,有了该导数后,根据链式法则就可以比较容易地求出 ∂C∂Wl 和 ∂C∂bl。
CNN 中的 BP 算法
之所以要「啰嗦」地回顾普通的 BP 算法,主要是为了熟悉一下链式法则,因为这一点在理解 CNN 的 BP 算法时尤为重要。
下面就来考虑如何把之前的算法套路用在 CNN 网络中。
CNN 的难点在于卷积层和 pooling 层这两种很特殊的结构,因此下面重点分析这两种结构的 BP 算法如何执行。
卷积层
假设我们要处理如下卷积操作:(a11a12a13a21a22a23a31a32a33)∗(w11w12w21w22)=(z11z12z21z22)
z11=a11w11+a12w12+a21w21+a22w22
z12=a12w11+a13w12+a22w21+a23w22
z21=a21w11+a22w12+a31w21+a32w22z22=a22w11+a23w12+a32w21+a33w22
上图的网络结构中,左边青色的神经元表示 a11 到 a33,中间橙色的表示 z11 到 z22。需要注意的是,青色和橙色神经元之间的权值连接用了不同的颜色标出,紫色线表示 w11,蓝色线表示 w12,依此类推。这样一来,如果你熟悉 BP 链式法则的套路的话,你可能已经懂了卷积层的 BP 是怎么操作的了。因为卷积层其实就是一种特殊的连接层,它是部分连接的,而且参数也是共享的。
假设上图中,z 这一层神经元是第 l 层,即 z=zl,a=al−1。同时假设其对应的误差项 δl=∂C∂zl 我们已经算出来了。下面,按照 BP 的套路,我们要根据 δl 计算 δl−1、∂C∂wl 和 ∂C∂bl 。
卷积层的误差项 δl−1
首先计算 δl−1。假设上图中的 al−1 是前一层经过某些操作(可能是激活函数,也可能是 pooling 层等,但不管是哪种操作,我们都可以用 σ() 来表示)后得到的响应,即 al−1=σ(zl−1)。那么,根据链式法则:δl−1=∂C∂zl−1=∂C∂zl∂zl∂al−1∂al−1∂zl−1=δl∂zl∂al−1⊙σ′(zl−1)
这里的重点是要计算 ∂zl∂al−1,这也是卷积层区别于全联接层的地方。根据前面展开的卷积操作的等式,这个导数其实比全联接层更容易求。以 al−111 和 al−112 为例(简洁起见,下面去掉右上角的层数符号 l):∇a11=∂C∂z11∂z11∂a11+∂C∂z12∂z12∂a11+∂C∂z21∂z21∂a11+∂C∂z22∂z22∂a11=δ11w11
(∇aij 表示 ∂C∂aij。如果这两个例子看不懂,证明对之前 BP 例子中的(1)式理解不够,请先复习普通的 BP 算法。)
其他 ∇aij 的计算,道理相同。
之后,如果你把所有式子都写出来,就会发现,我们可以用一个卷积运算来计算所有 ∇al−1ij:(00000δ11δ1200δ21δ2200000)∗(w22w21w12w11)=(∇a11∇a12∇a13∇a21∇a22∇a23∇a31∇a32∇a33)
卷积层的导数 ∂C∂wl 和 ∂C∂bl
这两项的计算也是类似的。假设已经知道当前层的误差项 δl,参考之前 ∇aij 的计算,可以得到:∇w11=∂C∂z11∂z11∂w11+∂C∂z12∂z12∂w11+∂C∂z21∂z21∂w11+∂C∂z22∂z22∂w11=δ11a11+δ12a12+δ21a21+δ22a22
∇w12=∂C∂z11∂z11∂w12+∂C∂z12∂z12∂w12+∂C∂z21∂z21∂w12+∂C∂z22∂z22∂w12=δ11a12+δ12a13+δ21a22+δ22a23
其他 ∇wij 的计算同理。
跟 ∇aij 一样,我们可以用矩阵卷积的形式表示:(a11a12a13a21a22a23a31a32a33)∗(δ11δ12δ21δ22)=(∇w11∇w12∇w21∇w22)
pooling 层
跟卷积层一样,我们先把 pooling 层也放回网络连接的形式中:
红色神经元是前一层的响应结果,一般是卷积后再用激活函数处理。绿色的神经元表示 pooling 层。很明显,pooling 主要是起到降维的作用,而且,由于 pooling 时没有参数需要学习,因此,当得到 pooling 层的误差项 δl 后,我们只需要计算上一层的误差项 δl−1 即可。要注意的一点是,由于 pooling 一般会降维,因此传回去的误差矩阵要调整维度,即 upsample。这样,误差传播的公式原型大概是:
δl−1=upsample(δl)⊙σ′(zl−1)。
下面以最常用的 average pooling 和 max pooling 为例,讲讲 upsample(δl) 具体要怎么处理。
假设 pooling 层的区域大小为 2×2,pooling 这一层的误差项为:δl=(2846)
∂average(x)∂xk=1m
因此,对 average pooling 来说,其误差项为:δl−1=δl∂average∂x⊙σ′(zl−1)=upsample(δl)⊙σ′(zl−1)=(0.50.5220.50.522111.51.5111.51.5)⊙σ′(zl−1)
参考
- How the backpropagation algorithm works
- 卷积神经网络(CNN)反向传播算法
- Convolutional Neural Networks backpropagation: from intuition to derivation
- 如何通俗易懂地解释卷积? - 马同学的回答 - 知乎
- https://www.slideshare.net/kuwajima/cnnbp