B样条曲线的一些基本性质

1.B样条曲线的节点（knot）指的是将区间划分为一段一段的分段点。节点向量（knot vector）则是由多个节点组成的向量，代表着对于这个B样条曲线是如何进行分段的。节节点（knot point）则是区间分段点所对应的B样条曲线上的曲线分段点。

2.B样条曲线的次数（degree）也就是基函数的次数，而阶数（oder）则是次数加1。基函数的次数就是多项式中x的最高的次数。

3.若B样条曲线由n+1个控制点（从P0到Pn），有m+1个节点（从u0到um），阶数为p+1（次数为p），则必须满足m=n+p+1。不同的文献中具体的符号表示不同，但是从本质上来说就是控制点的个数加上曲线的次数再加上1等于节点的个数。

4.B样条曲线的每个控制点对应一个基函数，所有控制点与对应的基函数的乘积求和可得到B样条曲线的函数表达式。基函数是通过下面两个式子递推而来的（也就是说高次的基函数其实归根结底都是由0次的基函数乘上一些系数组成的，这也决定了在某些区间内，基函数始终为0）：

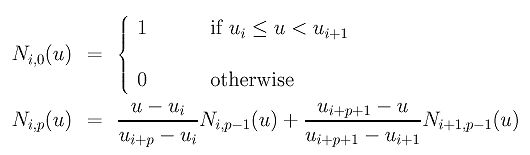
在计算时可采用下面的三角形来辅助理解：

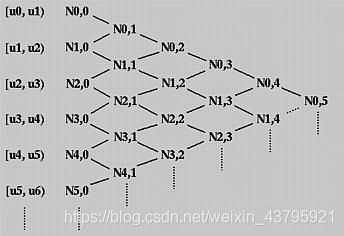
5.B样条曲线具有局部支撑性。

第i+1个控制点Pi只影响区间（ui，ui+p+1）之间的曲线（p是基函数的次数）。这一点可以根据下面的三角图来理解：

上图中的N1,3代表序号为1的控制点所对应的基函数，层层分解之后，可以知道其在[u1, u2), [u2, u3), [u3, u4) 和[u4, u5)上是非零的，也就是它在[u1, u5)上非零。而N1,3基函数在其他区间上取值都为0，也就是说无论N1,3基函数对应的控制点怎么取值，都对别的区间内的曲线没有影响（所以说B样条可以进行局部调整）。

总结一下就是：基函数 Ni,p(u) 在[ui, ui+p+1)上非零。或，相等地，Ni,p(u) 在 p+1个节点区间[ui, ui+1), [ui+1, ui+2), …, [ui+p, ui+p+1)上非零。

那么，反过来看如果我观察一个区间的话，这个区间内的曲线会受哪些基函数的影响呢？

类似地，可以通过下面的三角图去理解：

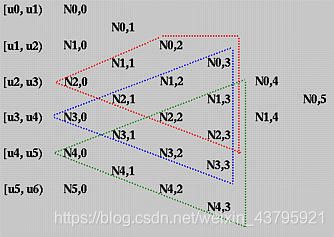
所有的高次基函数本质上都是由第一列的非0即1的0次基函数所组成的。对于区间 [u3, u4)来说，所有不在蓝色三角形内的别的高次基函数拆解为0次的基函数后，在 [u3, u4)上均为0，对该区间上的曲线没有任何的影响。所以，对该区间的曲线有影响的就只有三角形内的基函数了。

总结一下就是：在任何一个节点区间 [ui, ui+1), 最多有 p+1个p 次基函数非零，即：Ni-p,p(u), Ni-p+1,p(u), Ni-p+2,p(u), …, Ni-1,p(u) 和 Ni,p(u)。（且这些基函数的累加和为1）

6.强制第一个节点和最后一个节点的重复度为p+1，那么产生的曲线就会分别与第一个控制点和最后一个控制点的第一边和最后一边相切，且曲线会经过第一个控制点和最后一个控制点。也就是所谓的clamped B样条曲线。

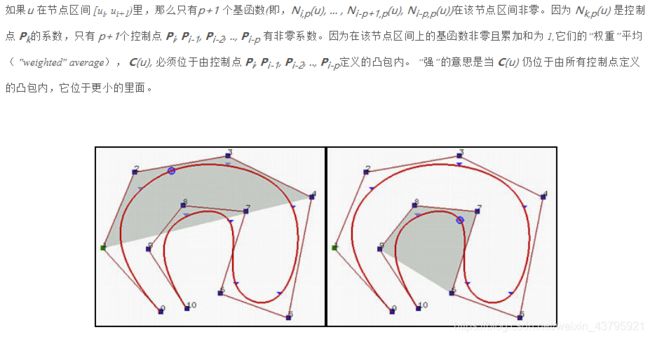
7.凸包性。样条曲线包含在控制折线（ployline）的凸包内。更特别地，如果u 在节点区间[ui,ui+1)里，那么C(u)在控制点Pi-p, Pi-p+1, …, Pi的凸包里。

点击即可打开链接：B样条曲线示例（可以通过移动控制点观察曲线的变化）