无人驾驶之车辆控制 (2)MPC模型预测控制算法
目录
- 引言
- 原理概要
- 数学推导
- 模型建立
- 目标函数
- 仿真结果
- 总结
引言

控制算法的作用在于保证被控系统能够在满足规定的性能需求(快速响应,稳定性,精确性等)的前提下,完成特定的任务。对无人车辆进行控制的本质就是将原先由驾驶员给出的方向盘转向动作、油门踏板以及脚刹的开合度转换为一连串的有固定控制周期的离散信号并输出给底盘的执行层。下文中要介绍的MPC算法是一种基于能够描述系统特性的数学模型,来组合出一串时间维度的上的控制量序列,最终保证车辆对目标轨迹贴合较好又舒适安全的控制算法。
原理概要
MPC的全称是模型预测控制(Model Predictive Control),简单来说就是利用一个现有模型来针对系统未来状态进行预测,同时决定应该采取什么样的动作能保证系统在接下来一段时间内的状态能与之前预测的相符合。让我来举两个简单的例子来说明MPC的原理:
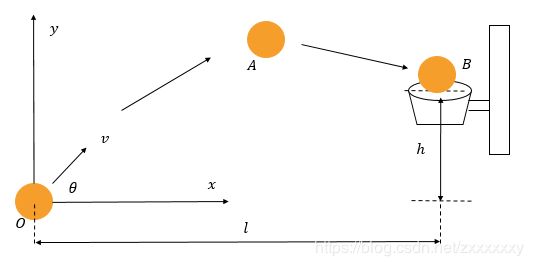
假如我们知道图中的这颗篮球出手那一瞬间,球的初始速度大小v以及方向θ,还有距离筐的水平距离l以及其相对高度h,根据高中学过的物理知识以及数学工具(模型)可以很轻松的计算出这颗篮球于任意时刻在空中的确切位置,以及它最终能否顺利入筐(状态预测)。反过来说,MPC可以根据篮筐相对于篮球的位置,来计算出球员应该以什么样的角度以及速度(计算对应控制量)投出这个球。
如果想要计算出来的预测控制量比较精确,那么往往需要更加精确的物理模型。比如在这投篮的这个例子中,我们会需要更细致地考虑空气阻力以及不同地理位置具有的不同重力加速度等因素对篮球投射过程的影响,而不只是简单地假设没有空气阻力存在以及球在空气中的水平速度保持不变。虽然更精准、完备的模型意味着更准确的预测以及更好的控制效果,但是往往在实际应用中还是只会采用比较简单的模型来近似处理,基本可以满足应用同时还能降低算法的复杂度以及对算力的要求。
上面的例子描述了MPC的基本思想,接下来的这个例子可以帮助我们熟悉本算法的许多特点。其实我们在下象棋中的思考过程与模型预测控制的运作方式也是十分相近的。
- 我们脑海里有既往下棋的经验。(模型)
- 不同的棋子都有自己的移动规则,比如炮要隔山打,马脚被堵就无法动弹,而且大家都不能下到棋盘外面。(约束)
- 我们的最终目标是要赢。(设置目标函数)
- 最好是在现有约束条件以及基于既有经验模型的条件下,想出一系列能用最少步数、棋子损失战胜对手的策略。(最优化求解)
- 我们需要尽可能的去预测对手再接下来5步乃至10步、20步的走法,并想出针对性的策略。正常来说只能算5步的人永远赢不了走1步看10步的,不过随着预测时域的增加,对计算能力的要求也会以指数增长。(预测时域的长短与控制效果)。

个人认为MPC和现阶段火热的AI神经网络最大的区别在于一个是由纯粹的物理或者化学等方面(取决于应用领域)的数学公式模型来驱动的,另一个则是由数据驱动的基础线性关系与激活函数叠加的庞大网络系统。但是两者的本质还是对于各种优化问题的求解:你有你的误差函数与梯度下降,我也有我的目标函数与二次规划。若想结果更精确,MPC需要建立与实际更接近、完善的数学模型;深层神经网络则需要更海量的数据。因此两者同样对硬件提供的矩阵运算能力有极高的要求,托了AI火热发展的东风,使得MPC算法有了在无人驾驶车辆上实现的硬件基础。
很明显,应用MPC的第一大难点就是针对被控对象建立合适的数学模型。因为现实很多场景是难以用数学语言去准确表达的,哪怕勉强弄出来一个模型,也会存在准确率不高的情况。并且哪怕你学会了MPC,如果要想将其应用到特定领域,那么没有相关行业的扎实的知识背景,也是很难提炼出一个好的数学模型。比如无人驾驶领域就需要你懂车辆动力学,车辆的轮胎特性等;MPC目前的主战场化工领域则要求你对整套工业生产的工艺流程以及最底层的化学反应过程有透彻的理解。
而DNN则更像是一个普适的大杀器。很多从业者不再需要挖掘出深埋在事物背后的那些复杂、晦涩的运作机理,只需在专家的带领下搭建一个基础的模型,喂入数据,做应用的难度大大降低。公司里比较常见的情况也是一个大神带着一票调参侠,在天量的数据和牛逼的硬件的帮助下弄出精度不低的网络模型来(真正做AI基础理论研究的研究员还是很了不起的,这里没有任何不敬的意思)。可以说DNN的发明与兴盛是顺应时代的,是伟大的;但也逐渐弱化了很多工程师对程序的掌控,沦为了机器与数据的工具人。呀跑远了,下面回到正题~
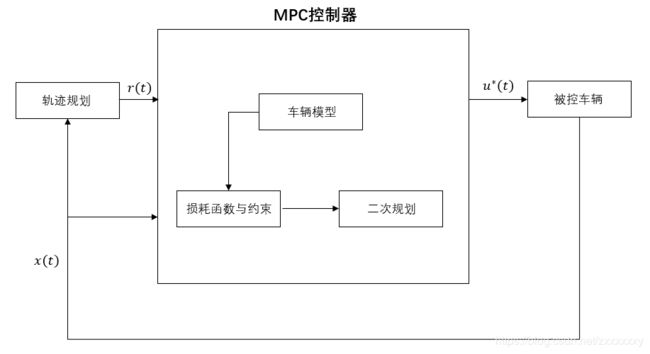
除了上面提到的数学模型之外,为了将其应用在无人驾驶车辆的控制上,MPC需要设计一个用来表征对车辆跟踪情况以及评估舒适性、效率性等性能指标的目标/损失(cost)函数,然后在不会发生安全事故以及超出车辆物理约束的前提下,求解出使得目标函数值最大或者最小的一组解(在有约束边界的有限解空间内寻找最优的方案)。
数学推导
结合论文[1]为例展开一下MPC在无人驾驶领域的应用方式以及公式推导。
模型建立
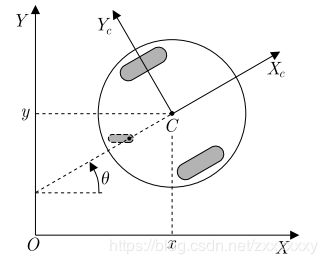
根据上述示意图建立简单的运动学模型:(1)
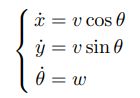
或者表达成一种更简洁的形式:(2)
![]()
| 符号 | 物理量 |
|---|---|
| x x x | 横坐标 |
| y y y | 纵坐标 |
| θ \theta θ | 航向角 |
| ω \omega ω | 横摆角速度 |
| v v v | 车速 |
| X X X | 状态量( x x x y y y ω \omega ω) |
| U U U | 控制量( ω \omega ω v v v) |
通过建立车辆参考方程来得到车辆的线性误差模型:(3)![]()
将(2)式在( X r X_r Xr, U r U_r Ur)附近做泰勒展开(忽略高阶项)可得:(4)
![]()
(3)(4)两式相减可得:(5)
![]()
其上:
![]()
![]()
对(5)式使用向前差分法得系统在离散时域下的线性模型:(6)
![]()
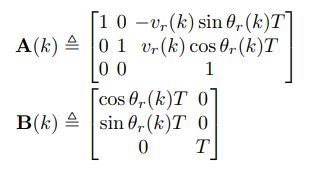
其中, T T T表示采样周期, k k k为采样间隔。
目标函数
经过上面的步骤,我们整了个还算靠谱的模型。而MPC的核心步骤是在有限的时长内(预测时域)对接下来输入到系统的控制量进行预测,以使系统靠近预设的目标状态。每次控制周期内,MPC控制器都会通过求解一个优化问题来计算出一序列的最优控制量组合。这个序列当中的第一组控制量会被实际施加到系统上,直到下一周期再次重复上述过程。因此随着预测时域不断前进,MPC总会基于车辆最新的状态来进行优化,保证理想的控制效果。所以本节要关注的重点就是针对用户需求来设计合适的目标函数供控制器进行这样一个滚动优化的过程。
以下是一个可供参考的目标函数形式:(7)
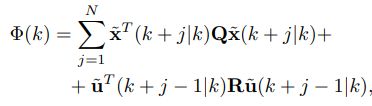
上式中的 Q Q Q与 R R R分别代表状态矩阵以及控制量矩阵的权重参数矩阵。
第一项的含义为对系统在预测时域中的实际状态与期望状态的误差进行优化,提高无人车辆对轨迹的跟踪能力。第二项对控制量进行优化,保证车辆行驶过程中的舒适性。
在长度为 N N N的预测时域内,状态矩阵与控制量矩阵的形式如下:(8)

应此,目标函数(7)可改写为:(9)
![]()
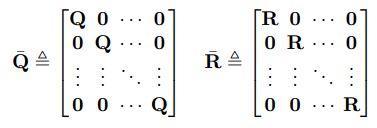
相应地,在 N N N的预测时域内,式 (6)改写为:(10)
![]()
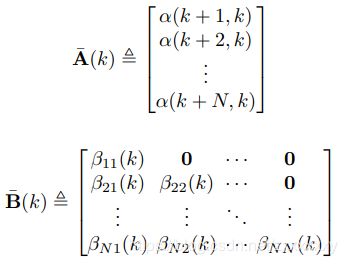
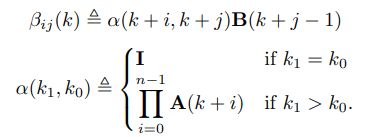
最后将目标函数(9)转换成方便进行优化求解的二次规划形式:(11)
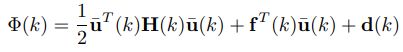
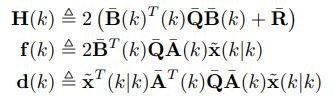
其中 H H H往往代表一个半正定或正定的海森矩阵,包括了二次规划求解的目标函数中的二次项。向量 f f f代表其线性项。 d d d为一独立项,对求解最优的控制量序列 u ∗ u^* u∗没有作用。
针对该优化问题:![]()
有如下约束:
![]()
这些约束量的最大最小值一般由车辆实际转向特性以及安全限速之类的决定。今后会专门另开一文来介绍该类二次规划的求解方法,此处暂且不表。
仿真结果
利用matlab做了个简单的仿真验证:

可以看到代表车辆的圆点较快地跟踪上了图中y=5的直线。
总结
模型预测控制关注的是接下来一段有限时域内的状态,预测时域的选取对预测与控制的效果有极大的影响。正如一位领袖如果目光不够长远,可能就会出现战术上胜利,战略上失败的情况。即局部最优解不一定是全局最优解。MPC所需的模型也不局限于数学模型,比如可以结合能够充分描述被控对象特性的神经网络模型。如果理论上存在一个能无限逼近现实的模型,那么MPC也能大放异彩。
[1] W.F. Lages, J. Augusto, and V. Alves. REAL-TIME CONTROL OF A MOBILE ROBOT USING LINEARIZED MODEL PREDICTIVE CONTROL. 2006
[2] 龚建伟,姜岩,徐威. 无人驾驶车辆模型预测控制 [M]. 北京理工大学出版社, 2014.4