牛客编程巅峰赛记录（C++）

简介

“牛客编程巅峰赛”是由牛客网面向所有求职者举办的全国性系列赛事活动，致力于帮助广大程序猿提高自己的编程能力，使程序猿们能在求职的过程中斩获自己心仪的offer。
在“牛客编程巅峰赛”，你不仅能快速提升自己，还能体会与人竞技的紧张与乐趣，并获得丰厚的奖励~

s1 第五场比赛20200723

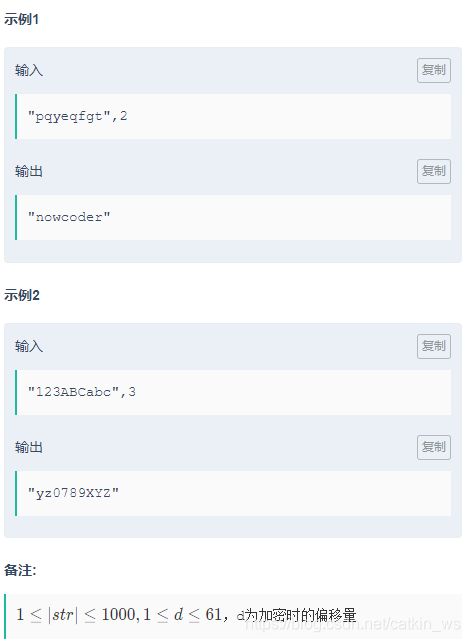
1 凯撒密码

class Solution {
public:
    /**
     * 解密密文
     * @param str string字符串 密文
     * @param d int整型 偏移量
     * @return string字符串
     *///0~61
    char num[62] = {'0','1','2','3','4','5','6','7','8','9',
                   'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M',
                   'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z',
                   'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm',
                   'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'};
    string decode(string str, int d) 
    {
        string res;
        if (str.empty())
            return res;
        for (int i = 0; i < str.size(); i++)
        {
            for (int j = 0; j < 62; j++)
            {
                 if (str[i] == num[j])
                 {
                     if (j - d < 0)
                         res.push_back(num[j+62-d]);
                     else
                         res.push_back(num[j-d]);
                 }
                    
            } 
        }// write code here
        return res;
    }
};

2 完全平方数的尾巴

主要在于证明 四位数以上的平方数不影响尾巴，故遍历999

class Solution {
public:
    /**
     * 
     * @param x int整型 
     * @return bool布尔型
     */
    bool solve(int x) 
    {
        // write code herewhile      
        for (int i = 0; i < 999; i++)
        {
            if ((i*i)%1000 == x)
                return true;
        }
        return false;
        
    }
};

s1 第六场比赛20200725

1循环右移

牛牛有一个二进制数的字符串，他想把字符串循环右移k位，然后得到一个新的二进制数，你能告诉牛牛这个数的十进制值是多少吗。给定一个二进制字符串str和循环位移位数k，返回循环后的二进制数的十进制值。

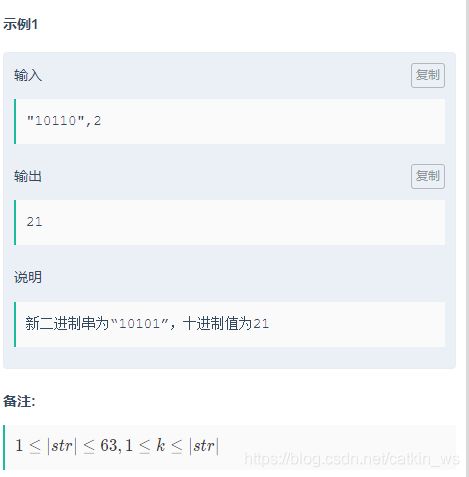
方法一：将循环部分字符串取出，放在剩余字符串的前面。

class Solution {
public:
    /**
     * 位移后二进制串的十进制值
     * @param str string字符串 二进制字符串
     * @param k int整型 循环位移次数
     * @return long长整型
     */
    long long rotateRight(string str, int k) 
    {
        // write code here
        long long num = 0;
        if (str.empty())
            return num;
        string res;
        int len = str.size();
        int yu = k % len;
        //reverse
        string first;
        string second;
        for (int i = 0; i < len; i++)
        {
            if (i >= len - yu)
                second += str[i];
            else
                first += str[i];
        }
        res = second + first;
        //2 to 10
        for (int i = 0; i < res.size(); i++)
	    {
            long long cur = pow(2,res.size() - 1 - i);
            num += cur*(res[i]-'0');
	    }
        return num;   
    }
};

方法二：第一部分翻转，第二部分反转；第一第二部分翻转

class Solution {
public:
    /**
     * 位移后二进制串的十进制值
     * @param str string字符串 二进制字符串
     * @param k int整型 循环位移次数
     * @return long长整型
     */
    long long rotateRight(string str, int k) 
    {
        long long num = 0;
        if (str.empty())
            return num;
        string res;
        int len = str.size();
        int yu = k % len;
        //reverse
        reverse(str.begin() + len - yu, str.end());
	    reverse(str.begin(), str.begin() + len - yu);//注意这里不是s.begin()+len-k-1
	    reverse(str.begin(), str.end());
        //2 to 10
        for (int i = 0; i < str.size(); i++)
	    {
            long long cur = pow(2,str.size() - 1 - i);
            num += cur*(str[i]-'0');
	    }
        return num;   
    }
};

2 牛牛爱奇数

在牛牛面前放着n个数，这些数字既有奇数也有偶数，只不过牛牛对奇数情有独钟，他特别想让这些数都变成奇数。
现在牛牛获得了一种能力，他可以执行一种操作：每次选中一个偶数，然后把这些数中与该数相等的数都除以2，例如现在有一个数组为$[2,2,3]$，那么牛牛可以执行一次操作，使得这个数组变为$[1,1,3]$。
牛牛现在想知道，对于任意的n个数，他最少需要操作多少次，使得这些数都变成奇数？

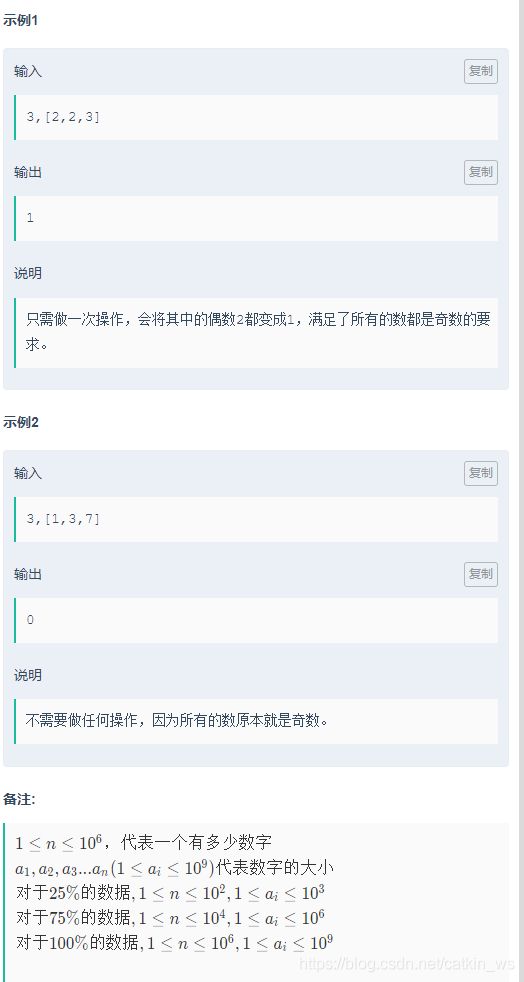
暴力求解：

class Solution {
public:
    /**
     * 返回一个数，代表让这些数都变成奇数的最少的操作次数
     * @param n int整型 代表一共有多少数
     * @param a int整型vector 代表n个数字的值
     * @return int整型
     */
    int solve(int n, vector<int>& a) 
    {
        // write code here
        set<int> res;
        for (int i = 0; i < a.size(); i++)
        {
            while (a[i] % 2 == 0)
            {
                res.insert(a[i]);
                a[i] /= 2;
            }
        }
        return res.size();
    }
};

解法二：

class Solution {
public:
    /**
     * 返回一个数，代表让这些数都变成奇数的最少的操作次数
     * @param n int整型 代表一共有多少数
     * @param a int整型vector 代表n个数字的值
     * @return int整型
     */
    int solve(int n, vector<int>& a) 
    {
        // write code here
        map<int, int> mp;
        priority_queue<int> q;
        int num = 0;
        for (int i = 0; i < a.size(); i++)
        {
            if (a[i] % 2 == 0)
            {
                if (mp[a[i]] == 0)
                    q.push(a[i]);
                mp[a[i]]++;
            }
        }
        while (!q.empty())
        {
            num++;
            int t = q.top();
            q.pop();
            if (t/2 %2 == 0)
            {
                if (mp[t/2] == 0)
                    q.push(t/2);
                //mp[t/2]++;
                mp[t/2]++;
            }
        }
        return num;
        /*//way2
        set res;
        for (int i = 0; i < a.size(); i++)
        {
            while (a[i] % 2 == 0)
            {
                res.insert(a[i]);
                a[i] /= 2;
            }
        }
        return res.size();*/
        
    }
};

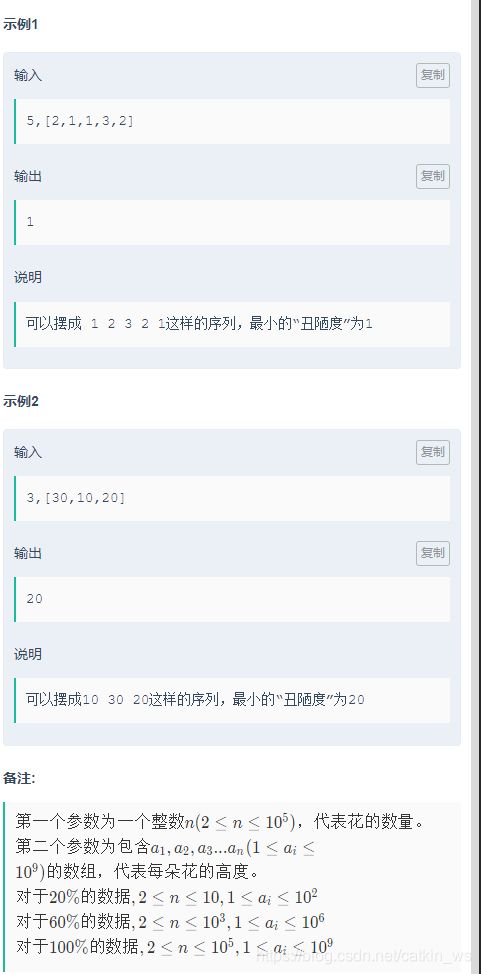
3 牛牛摆放花

牛牛有n朵需要摆放的花，但是每朵花呢，高度都不一样，牛牛不喜欢相邻的花高度相差太多，这样会影响美感。
所以牛牛提出了一个“丑陋度”的概念，“丑陋度”意思为在一个摆放序列中，相邻花高度差的最大值。而且牛牛是一个完美主义者，所以他希望:

• 将这些花摆成首尾相接的圆形
• 为了美观，他希望摆放的花“丑陋度”最小

程序应返回：按照这些花排成一个圆的顺序，输出在多个摆放花的序列中，最小的“丑陋度”。

class Solution {
public:
    /**
     * ​返回按照这些花排成一个圆的序列中最小的“丑陋度”
     * @param n int整型 花的数量
     * @param array int整型vector 花的高度数组
     * @return int整型
     */
    int solve(int n, vector<int>& array) 
    {
        // write code here
        if (array.empty() || n <= 1)
            return 0;
        int max = 0;
        int len = array.size();
        vector<int> ji;
        vector<int> ou;
        sort(array.begin(), array.end());
        for (int i = 0; i < len; i++)
        {
           if (i%2 == 0)
               ou.push_back(array[i]);
            else
                ji.push_back(array[i]);
        }
        reverse(ji.begin(), ji.end());
        array.clear();
        for (int i = 0; i < ou.size(); i++)
        {
           array.push_back(ou[i]);
        }
        for (int i = 0; i < ji.size(); i++)
        {
           array.push_back(ji[i]);
        }
        for (int i = 0; i < array.size() - 1; i++)
        {
            if (abs(array[i] - array[i+1]) > max)
                max = abs(array[i] - array[i+1]);
        }
        int max1 = abs(array[0] - array[len-1]);
        if (max1 > max)
            max= max1;
        return max; 
    }
};

s1 第七场比赛20200730

1 牛牛闯关（深度搜索DFS）

身为屯里第一剑士的牛牛来到训练场里闯关，由于过于勤奋，牛牛的宝剑的耐久度降到了 2 ，这意味着牛牛最多只能打倒两只怪兽，否则将会被淘汰。

训练场的地图可以看作一棵以 1 为根节点的树，训练场的终点为这棵树的叶子结点，树上的每个结点最多有一只怪兽，结点与结点间的边上没有怪兽。

每一个有怪兽的结点上牛牛都需要打倒怪兽才算安全，并且牛牛一旦选定好打怪路线之后便不能走回头路。

请问牛牛有多少种到达终点且不被淘汰的路径。

DFS深度优先搜索

/**
 * struct Point {
 *	int x;
 *	int y;
 * };
 */

class Solution {
public:
    /**
     * 返回牛牛能到达终点且不被淘汰的路径数
     * @param n int整型 
     * @param Edge Point类vector 
     * @param f int整型vector 
     * @return int整型
     */
    vector<vector<int> >v;
    vector<int>vis,val;
    int ans;
    
    bool check(int id)
    {
        for(int i=0;i<v[id].size();i++)
            if(vis[v[id][i]]==0)return 0;
        return 1;
    }
    
    void dfs(int id,int sum)
    {
        if(sum>2) 
            return;
        if(check(id))
            ans++;
        
        for(int i=0;i<v[id].size();i++)
        {
            if(vis[v[id][i]]==0)
            {
                vis[v[id][i]]=1;
                dfs(v[id][i],sum+val[v[id][i]]);
            }
          
        }
    }
    
    int solve(int n, vector<Point>& Edge, vector<int>& f) 
    {
        // write code here
        ans=0;
        v.resize(n+1);
        vis.resize(n+1);
        val.resize(n+1);
        for(auto it:Edge)
        {
            v[it.x].push_back(it.y);
            v[it.y].push_back(it.x);
        }
        for(int i=1;i<=n;i++)
        {
            vis[i]=0;
            val[i]=f[i-1];
        }
        vis[1]=1;
        dfs(1,val[1]);
        return ans;
    }
};

s1 第八场比赛20200801

1 牛牛的分配

注意，当sum数值较大，用long long 替换 int

在牛牛面前有n个瓶子，每个瓶子的大小体积都一样，但是每个瓶子内的含水量都不相同。

因为牛牛是个完美主义者，他希望瓶子中的水能够满足他的要求，他的要求是瓶子中的水最少为x。所以他打算对这些瓶子里的水进行重新分配，以满足最多的瓶子中水量大于等于x。

牛牛的分配规则是：每次可以选择多个瓶子，将里面的水平均分配到已选择的瓶子中。

给定n个瓶子和牛牛的对瓶中的水量要求xx，以及n个瓶子中的含水量，求最多可以有多少个瓶子满足牛牛的要求？

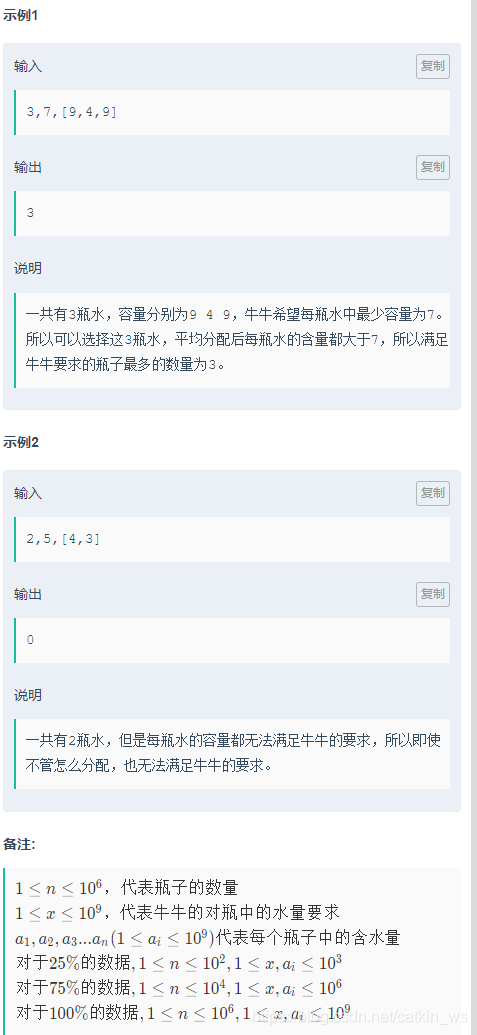
先排序所有的水，瓶子的数量是 int型，每瓶水的理想高度x也是int 型，但是总水量可能是long long！

排序完之后，从最大水量的那一瓶开始，看满足要求吗，满足则记录当前 理想瓶数，并计算第二大瓶的水量，总水量再平均是否满足要求。以此类推，直至水量遍历完。

class Solution {
public:
    /**
     * 返回重新分配后，满足牛牛要求的水量的瓶子最多的数量
     * @param n int整型 瓶子的数量
     * @param x int整型 牛牛的对瓶中的水量要求
     * @param a int整型vector 每个瓶子中的含水量
     * @return int整型
     */
    int solve(int n, int x, vector<int>& a) 
    {
        // write code here
        if (a.empty() || n <= 0 || x <= 0)
            return 0;
        sort(a.begin(), a.end());
        long long sum = 0;
        int len = a.size();
        int res = 0;
        for (int i = len - 1; i >= 0; i--)
        {
            sum += a[i];
            if (sum >= (long long)((len - i) * x)) 
                res++; 
        }
        return res;
    }
};

方法二：

class Solution {
public:
    /**
     * 返回重新分配后，满足牛牛要求的水量的瓶子最多的数量
     * @param n int整型 瓶子的数量
     * @param x int整型 牛牛的对瓶中的水量要求
     * @param a int整型vector 每个瓶子中的含水量
     * @return int整型
     */
    vector<int> water;
    
    static bool compare(int a,int b)
    {
        return a < b; //升序排列，如果改为return a>b，则为降序
    }
    
    int solve(int n, int x, vector<int>& a)
    {
        // write code here
        int res = 0;
        if (a.empty() || n <= 0 || x <= 0)
            return res;
        int len = a.size();
        long long sum = 0;
        int num = 0;
        for (int i = 0; i < len; i++)
        {
            if (a[i] < x)
            {
                num++;
                water.push_back(a[i]);
            }
            sum += a[i];
        }
         
        if (sum == 0) return 0;
        if (num == len) return 0;
         
        sort(water.begin(), water.end(), compare);
         
        if (sum / len >= x)
        {
            res = len;
        }
        else
        {
            int length = len;
 
            for (int i = 0; i < num; i++)
            {
                sum = sum - water[i];
                length--;
                
                if (length == 0 || sum == 0)  return 0;
                
                if (sum / length >= x)
                {
                    res = length;
                    break;
                }
            }
        }
        return res;
    }
};

s1 第九场比赛20200806

又是被虐的一场，哎…

1 牛牛的木板

牛牛从牛毕那里拿了一根长度为n的白木板，木板被等分成了n段（没有被切割，只是虚拟划分成了n段），其中有些段被牛毕用颜料染成了黑色。

牛牛非常不喜欢黑色，它找来了一桶清洗剂决定对木板进行清洗，但是牛牛发现自己的清洗剂最多只能清洗m段。

清洗完后，牛牛会把木板锯成纯色的几段。例如假设木板是 （黑黑黑白白白白黑黑黑 ），就会被锯成（黑黑黑）（白白白白）（黑黑黑）三段。

牛牛想知道，它足够聪明地清洗木板，能获得的纯白色木板的最大长度是多少。

正确思路：双指针…类似，子数组最大和
找到[left，right]之间的黑点数小于等于m的区间。

• 左指针不动，右指针随着遍历前进
• 当前为黑点，num++
• 如果num > 洗涤剂m
• 左指针移动（当前左指针为黑点的话，洗涤剂num–）
• 记录当前的最大值

class Solution {
public:
    /**
     * 
     * @param n int整型 
     * @param m int整型 
     * @param a int整型vector 
     * @return int整型
     */
    int solve(int n, int m, vector<int>& a) 
    {
        // write code here
        int left = 0;
        int num = 0;
        int max = 0;
        for (int i = 0; i < n; i++)
        {
            if (a[i] == 0)
                num++;
            while (num>m)
            {
                if (a[left] == 0)
                {
                    num--;
                   
                }   
                left++;
            }
            if (i -left + 1 > max)
                max = (i - left + 1);
        }
        return max;
    }
};

我的思路：狗血…

1. num个黑点，m个洗涤剂，随机洗白m个黑点（类似全排列）
2. 比如[1,0,0,1,1,1]
3. 找出黑点所在索引a[1],a[2]
4. 将[1,2]进行全排列，得到[1,2],[2,1];
5. 只能洗白1个，则do while循环中，每次将木板前m个索引处洗白
6. 洗完后，搜索当前最长的白段（O(n)，一个for循环）
7. 本地测试通过，但是算法循环太长~~~~~~~

class Solution {
public:
    /**
     * 
     * @param n int整型 
     * @param m int整型 
     * @param a int整型vector 
     * @return int整型
     */
    int solve(int n, int m, vector<int>& a) 
    {
        // write code here
        if (a.empty())
            return 0;
        int num = 0;
        int res = 0;
        int len = 0;
        int max = 0;
        vector<int> label;
        for (int i = 0; i < a.size(); i++)
        {
            if (a[i] == 0)
            {
                num++;
                label.push_back(i);
            }
        }
        
        int* shuzu = new int[num];
        sort(label.begin(), label.end());
        for (int i = 0; i < label.size(); i++)
        {
                shuzu[i] = label[i];
        }
        
        if (m >= num)
            res = a.size();
        else
        {
            //label select m to 1;
            do
            {
                vector<int> aa = a;
			    len = 0;
                
                for (int i = 0; i < m; i++)
                {
                    aa[shuzu[i]] = 1;
                }
                 for (int i = 0; i < aa.size(); i++)
                {
                    if (aa[i] == 1)
                    {
                        len++;
                        if (len > max)
                            max = len;
                    }
                    else
                        len = 0;
                }
            }while(next_permutation(shuzu, shuzu+num));
            res = max;
            //res = search(n, m, a);
        }
        return res;
    }
};

s1 第十场比赛20200808

1 牛牛排队

下课了，牛牛要去食堂吃饭，他们学校的食堂有很多个门，而且整个建筑物是圆形的。只不过要去吃饭的人很多，在里面吃饭的人也很多，所以大家都在门口外面排队等待吃饭。

所以牛牛采取了这样的一个策略：刚开始时，牛牛在第一个门口，如果这个门口有人在排队，那么他选择花费1分钟时间走到下一个门口，如果没有人的话，牛牛就可以直接进去吃饭啦。食堂的每一个门，每1分钟排队的人数都会减少一个。

现在给你门的数量n，和每个门外排队的人的数量，如果按照牛牛的策略，那么牛牛最终会在哪个门进去吃饭呢？请你进行编程求解，返回牛牛最终是从第几个门进入食堂吃饭的。

思路：当前不是0，则所有门外的人数-1，牛牛位置加1，再次判断

• 经过n步（n>=0),牛牛必在为0的门左边或者右边进入
• 首选判断数组最小值
• 数组每个都减去最小值
• 经历减去最小值的步，到达cur下标处（如果当前a[cur]=0,直接返回）
• 当前cur处数组不为0，进行while循环：
• 数组中所有非0的人数减一
• cur++
• cur大于数组下标，返回到初始位置0
• while循环判断当前cur处值
• 迭代结束，返回

class Solution {
public:
    /**
     * 返回牛牛最终是从第几个门进入食堂吃饭的
     * @param n int整型 代表门的数量
     * @param a int整型vector 代表每个门外等待的人数
     * @return int整型
     */
    int solve(int n, vector<int>& a) 
    {
        // write code here
        int min = a[0];
        int label = 0;
        int res = 0;
        int num=0;
        for (int i = 0; i < a.size(); i++)
        {
            if (a[i] < min)
            {
                label = i;
                min = a[i];
            }
        }
        for (int i = 0; i < n; i++)
		{
			a[i] = a[i] - min;
		}
        int cur = min%n;
        if (a[cur] == 0)
            return cur+1;
       	while (a[cur] != 0)
        {
            for (int i = 0; i < n; i++)
            {
                if (a[i] > 0)
                    a[i]--;
            }
            cur++;
            if (cur  == n)
                cur = 0;
        }
        return cur+ 1;
    }
};

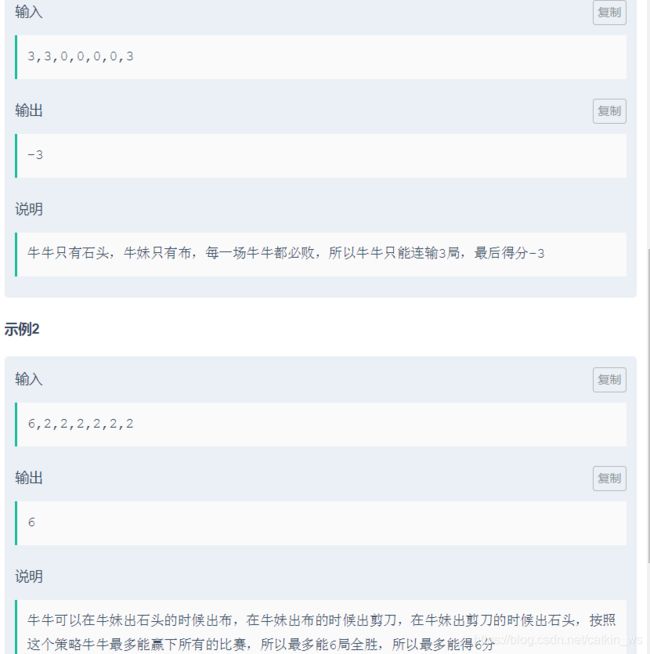
2 石头剪刀布

牛牛为了让牛妹崇拜他，决定和牛妹进行石头剪刀布游戏。

当然，普通的石头剪刀布根本吸引不到牛妹，也无法展现牛牛高超的能力，所以牛牛想起了他在一本漫画中看到的规则，游戏规则如下：

两个人进行石头剪刀布大战，开始时会发给每个人n张牌，然后两人进
行n次剪刀石头布大战，每一次两人分别选择自己的n张牌中的一张，打出，每张牌只能用一次。

牛牛每赢一局会+1分，每输一局会-1分，每平局一局不加分也不减分。
牛牛这个游戏已经玩到了出神入化的地步，以至于他能猜到每一次牛妹会出什么牌。请问在知道牛妹每一轮出什么牌的情况下，牛牛最终的分数最高多少分？

开始发给牛牛的n张牌里，有p1张石头牌，q1张剪刀牌，m1张布牌。
开始发给牛妹的n张牌里，有p2张石头牌，q2张剪刀牌，m2张布牌。

请返回牛牛的最高得分

比较简单，贪心策略：

求牛哥 赢的局+平的局+输的局 即可

赢的局：

• 牛哥石头与牛妹剪刀
• 牛哥剪刀与牛妹布
• 牛哥布与牛妹石头

平的局：

• 牛哥剩下的石头与牛妹剩下的石头
• 牛哥剩下的剪刀与牛妹剩下的剪刀
• 牛哥剩下的布与牛妹剩下的布

输的局，牛哥剩下多少输多少。

代码如下：

class Solution {
public:
    /**
     * 
     * @param n int整型 
     * @param p1 int整型 
     * @param q1 int整型 
     * @param m1 int整型 
     * @param p2 int整型 
     * @param q2 int整型 
     * @param m2 int整型 
     * @return int整型
     */
    int Highestscore(int n, int p1, int q1, int m1, int p2, int q2, int m2) 
    {
        // write code here
        int num1  = min(p1, q2);
        int num2  = min(q1, m2);
        int num3  = min(m1, p2);
        
        p1 = p1 - num1;  q2 = q2 - num1;
        q1 = q1 - num2;  m2 = m2 - num2;
        m1 = m1 - num3;  p2 = p2 - num3;
        
        int num4  = min(p1, p2);
        int num5  = min(q1, q2);
        int num6  = min(m1, m2);
        
        p1 = p1 - num4;  p2 = q2 - num4;
        q1 = q1 - num5;  q2 = q2 - num5;
        m1 = m1 - num6;  m2 = m2 - num6;
        
        return num1+num2+num3-p1-q1-m1;    
    }
};

s1 第十一场比赛20200813

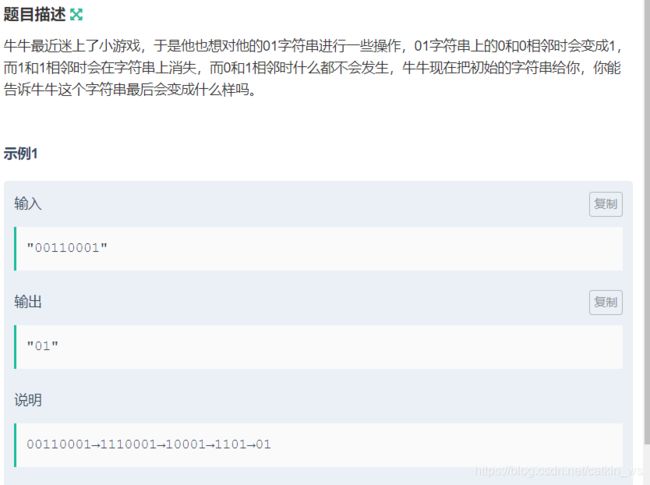
牛牛的01消消乐

class Solution {
public:
    /**
     * 
     * @param str string字符串 初始字符串
     * @return string字符串
     */
    string solve(string str) 
    {
        // write code here
        
        if (str.empty())
            return str;
        string s;
        for (auto i : str)
        {
            if (s.empty())
            {
                s.push_back(i);
            }
            else if (s.back() == i && i == '0')
            {
                s.pop_back();
                if (!s.empty() && s.back() == '1')
                {
                    s.pop_back();
                }
                else
                {
                    s.push_back('1');
                }
            }
            else if (s.back() == i && i == '1')
            {
                s.pop_back();
            }
            else
            {
                s.push_back(i);
            }
        }
        //string res;
       // for (auto i : s)
        //    res+=i;
        //return res;
        return s;
    }
};

s1 第十一场比赛20200815

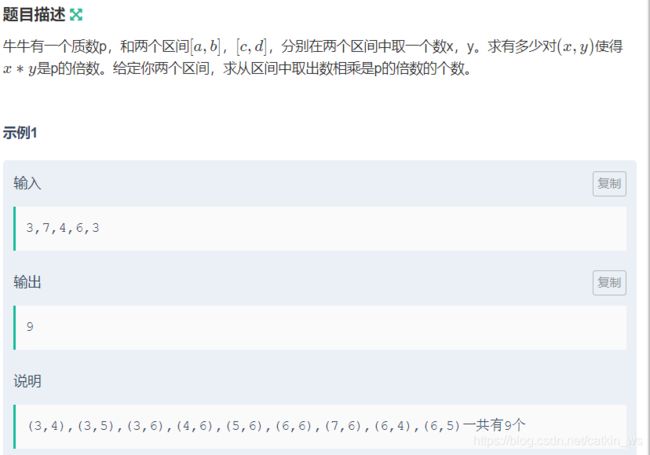
1 给定两区间内两数乘积是质数p的倍数

class Solution {
public:
    /**
     * 返回两个区间内各取一个值相乘是p的倍数的个数
     * @param a int整型 第一个区间的左边界
     * @param b int整型 第一个区间的右边界
     * @param c int整型 第二个区间的左边界
     * @param d int整型 第二个区间的右边界
     * @param p int整型 质数
     * @return long长整型
     */
    long long numbers(int a, int b, int c, int d, int p) {
        // write code here
        long long num1 = b / p - (a - 1) / p;
        long long num2 = d / p - (c - 1) / p;
        long long len1 = b - a + 1;
        long long len2 = d - c + 1;
        long long ans = num1 * len2 + num2 * len1 - num1 * num2;
        return ans;
    }
};

自己的方法，超时了：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
	long long a = 3, b = 7, c = 4, d = 6;
	long long p = 3;
	
	map<long long, long long> result;

	long long ans = 0;
	long long min = a * c;
	long long max = b * d;
	long long begin = min / p;
	long long cur_val = begin * p;
	if (cur_val < min)
	{
		begin++;
		cur_val = begin * p;
	}
	if (cur_val > max)
		return ans;
	while (cur_val >= min && cur_val <= max)
	{
		for (long long i = a; i <= b; i++)
		{
			if (cur_val % i == 0)
			{
				//if (result[cur_val/i] != 0)
					//ans++;
				result[cur_val / i]++;
			}
		}
		begin++;
		cur_val = begin * p;
	}
	for (long long i = c; i <= d; i++)
	{
		if (result[i] > 0)
			ans += result[i];
	}
	cout << ans;
	system("pause");
	return 0;
}