浅谈C++中Char、int和flaot在计算机中的表示
浅谈C++中Char、int和flaot在计算机中的表示
在实际计算机内存中char、int和float是怎么存储的关系到我们正确认识这些C++编程语言built-in的数据内型,以前读书没怎么关注这些,现自己总结下,关键点是flaot数。
1、Char
在32Bit的系统中,char占用1Byte。其实char是一种特定的int型数据,具体的见int。在计算机的内存中C++的char型数据存储的是该字符的ASCII码值,这点切记。
2、int
Int型是大家最熟悉的,通常在计算机中int型是以该数的二进制补码表示的(一个数怎么怎么求原码、补码等,自己复习),这是因为二进制补码具有高度的一致性,能够简化数据的加减乘除运算(计算机原理知识)。
35 00100011
+12 00001100
+ 47 00101111
注意都是表示为8bits二进制。负数的补码是原码“取反加一”,如:
35 00100011
-12 11110100
23 00010111
上面是35 - 12,由于负数的补码是原码“取反加一”,所以相当于是35+ (-12),且(-12)补码 = 11110100,注意这里的进位直接忽略。
在二进制中左移1位相当于乘以2,右移相当于除以2。所以这样就很方便了乘法器和除法器的设计了(但实际比这要复杂)。显然可以从这里看出来,在整数进行除法运算的时候,由于没有小数位,所以两个int型相除的时候,直接忽略小数位,没有“四舍五入”法则。
Int数据表示范围表
| 类 型 |
字节数 |
位数 |
表 示 范 围 |
|
| 下 限 |
上 限 |
|||
| char |
1 |
8 |
-128 |
127 |
| signed char |
1 |
8 |
-128 |
127 |
| unsigned char |
1 |
8 |
0 |
255 |
| short int |
2 |
16 |
-32768 |
32767 |
| signed short int |
2 |
16 |
-32768 |
32767 |
| unsigned short int |
2 |
16 |
0 |
65535 |
| int |
4 |
32 |
-2147483648 |
2147483648 |
| signed int |
4 |
32 |
-2147483648 |
2147483648 |
| unsigned int |
4 |
32 |
0 |
4294967295 |
| Long int |
4 |
32 |
-2147483648 |
2147483648 |
| signed long int |
4 |
32 |
-2147483648 |
2147483648 |
| unsigned long int |
4 |
32 |
0 |
4294967295 |
注意:在C++的int中表示的数字是该数字的二进制数。
3、Float
在十进制中float很多时候是用科学记数法来表示的。在计算机中同样想整形数一样表示为二进制,因为计算机只认识0和1。比如36.5可以表示为:
36.5 = 100011.100110011001...(1001循环,怎么转化是自己的事)
= 1.00011100110011001... X 25
当将数据转化成二进制后,float需要像十进制那样进行规格化,以便计算机表示。二进制float数的规格化是通过调整float的阶码使得该数的有效值在1和2之间,也即保证二进制数的整数部分为1。
(0.875)10 = (0.111)2 = 1.11 × 2-1
在计算机的内部,float是采用了IEEE754标准的形式来表示。将二进制数分成3段,分别为符号段,占1位、阶码段和尾数位。下面分别是32位系统的float和64位系统的float内部表示:
| 1 |
阶码位(8) |
尾数位(23) |
| 1 |
阶码位(11) |
尾数位(52) |
在上图中分别是32位系统中float的符号位占1位,阶码占8位,尾数位为23位,64位的系统中符号位还是占1位,阶码占11位,尾数为52位。
在十进制的浮点数的规格化中,要求写成小数点前不含有效数字,而且小数点后第一位为非0数字。比如
306.5 = 0.3065 × 103
二进制浮点数和十进制浮点数一样规格化,要求小数点后第一位为非0,也即只能为确定的1,这样这个确定的1构成了小数的尾数部分,从而在计算机表示float数中占用了宝贵的表示精确度的一位,所以在实际的内存表示中将这一位挪前。如:
(0.875)10 = (0.111)2 = 1.11 × 2-1;
这样在32位的系统中float的23位尾数是不是多表示了一位精度。
在计算机的具体实现中将哪个1抹去,在取出这个数进行计算的时候,自动加上一个1。但这样实现后,我们发现总有一个1,也就是即使尾数位全部是0,这个浮点数的有效值也为1,这样我们float就没法表示float型的0了。
所以在标准的32位float规定:浮点数的阶码为8位,阶值在-126~127;另外两个值,-127和-128用来表示特殊的浮点数。其中-127表示阶码为-126的非规格化数,非规格化数就是不做规格化的二进制浮点数,也就是说,有效值不省略小数点前面的1,之用23位尾数。因为0乘上任何2的阶数都为0,所以,当非规格化数的尾数全为0时,该数就是浮点0(前提是阶码为-127)。另外,当阶码为-128时,表示的数是非法操作的数(称其为NaN,即Not a Number之意)或者无穷大。
为了使浮点数0与整数0统一,即位码全0表示0。标准单精度浮点数对所有规格化和非规格化二进制数阶码一律做+127的偏移操作,在取出的时候,再做一个-127的逆操作。如:
36.5 = 100011.1001(2)
= 1.00011100110011001100110 × 25
= 0,10000100,000011100110011001100110(机内表示)
其中用两个逗号将浮点数分隔成符号位,阶码位和尾数位。阶码位的10000100为指数5加上127所得数的二进制表示。
好了,理论是写完了,帖实际的代码分析的看看。
#include
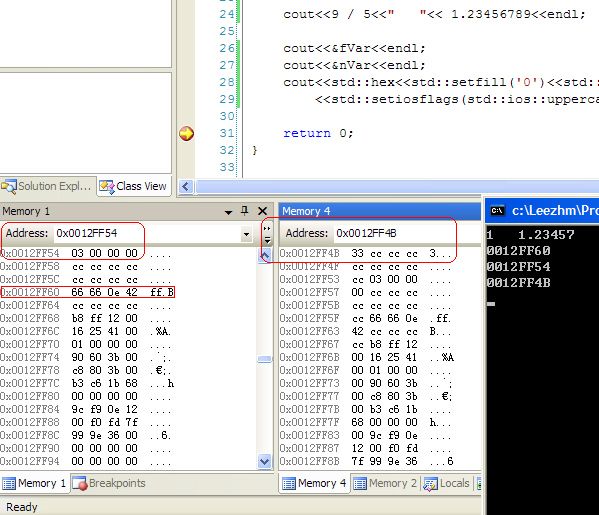
调试结果贴图:
1、输出1说明在整数进行除法运算的时候,由于没有小数位,所以两个int型相除的时候,直接忽略小数位,没有“四舍五入”法则。
2、输出1.23457说明有效值为6位,截断的时候有“四舍五入”法则。23位尾数表示有效数字。
3、0012FF60地址表示的 66 66 0e 42这个十六进制的正确排列是42 0e 66 66(注意是先高位地址后低位地址)换算成二进制为:
01000010 00001110 01100110 01100110
= 0,10000100,00011100110011001100110
10000100 = 132 = 127 + 5 (5就是36.5规格化后的指数)
4、0012FF54地址表示的就是整数3,说明整数存储的是该数值的二进制值。
5、0012FF54地址表示的就是字符3,33 cc cc cc正确排列就是cc cc cc 33,cc是填充字符,为不确定。33(16) = 51(10) 刚好就是字符3的ASCII值。
最后结合分析想想浮点数与0比较为什么不能直接==0.0?