2018 ICPC Asia Jakarta Regional Contest

A. Edit Distance

Description:

A binary string is a non-empty sequence of $0$'s and $1$'s, e.g., 010110, 1, 11101, etc. The edit distance of two binary strings $S$ and $T$, denoted by $edit(S,T)$, is the minimum number of single-character edit (insert, delete, or substitute) to modify $S$ into $T$. For example, the edit distance of 0011 and 1100 is $4$, i.e. 0011 $\to$ 011 $\to$ 11 $\to$ 110 $\to$ 1100. The edit distance of 1100101 and 1110100 is $2$, i.e. 1100101 $\to$ 1110101 $\to$ 1110100.
Ayu has a binary string $S$. She wants to find a binary string with the same length as $S$ that maximizes the edit distance with $S$. Formally, she wants to find a binary string $T_{max}$ such that $|S|=|T_{max}|$ and $edit(S,T_{max})\ge edit(S,T^{\prime })$ for all binary string $T^{\prime }$ satisfying $|S|=|T^{\prime }|$.
She needs your help! However, since she wants to make your task easier, you are allowed to return any binary string $T$ with the same length as $S$ such that the edit distance of $S$ and $T$ is more than half the length of $S$. Formally, you must return a binary string $T$ such that $|S|=|T|$ and $edit(S,T)>\frac{|S|}{2}$.
Of course, you can still return $T_{max}$ if you want, since it can be proven that $edit(S,T_{max})>\frac{|S|}{2}$ for any binary string $S$. This also proves that there exists a solution for any binary string $S$. If there is more than one valid solution, you can output any of them.

Input:

Input contains a binary string $S$ ($1\le |S|\le 2000$).

Output

Output in a line a binary string $T$ with the same length as $S$ that satisfies $edit(S,T)>\frac{|S|}{2}$.

Sample Input:

0011

Sample Output:

1100

Sample Input:

1100101

Sample Output:

0011010

题目链接

一个只含有0、1字符的字符串 $s$ 可以进行删除、添加和更改操作，构造另一只含有0、1字符的字符串使得原 $s$ 需进行 $\frac{|s|}{2}$ 以上步操作才可变为此字符串

分类讨论瞎搞……莫名其妙就过了

AC代码:

#include 

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0); std::cout.tie(0);

  std::string str; std::cin >> str;
  int max = 0, cnt0 = str[0] == '0', cnt1 = str[0] == '1'; char c;
  for (int i = 1, cur = 1; i < (int)str.length(); ++i) {
    if (str[i] == str[i - 1]) cur++;
    else cur = 1;
    if (cur > max) {
      max = cur;
      c = str[i];
    }
    cnt0 += str[i] == '0';
    cnt1 += str[i] == '1';
  }

  if (max == 1) {
    if (str[0] == '0') {
      std::cout << 1;
      for (int i = 1; i < (int)str.length(); ++i) std::cout << 0;
      std::cout << '\n';
    }
    else {
      std::cout << 0;
      for (int i = 1; i < (int)str.length(); ++i) std::cout << 1;
      std::cout << '\n';
    }
  }
  else if (max > (int)str.length() / 2) {
    if (c == '0') {
      for (int i = 0; i < (int)str.length(); ++i) std::cout << 1;
      std::cout << '\n';
    }
    else {
      for (int i = 0; i < (int)str.length(); ++i) std::cout << 0;
      std::cout << '\n';
    }
  }
  else if (cnt0 > (int)str.length() / 2) {
      for (int i = 0; i < (int)str.length(); ++i) std::cout << 1;
      std::cout << '\n';
  }
  else if (cnt1 > (int)str.length() / 2) {
    for (int i = 0; i < (int)str.length(); ++i) std::cout << 0;
    std::cout << '\n';
  }
  else if (max == (int)str.length() / 2) {
    if (c == '0') {
      for (int i = 0; i < (int)str.length() - 1; ++i) std::cout << 1;
      std::cout << 0;
      std::cout << '\n';
    }
    else {
      for (int i = 0; i < (int)str.length() - 1; ++i) std::cout << 0;
      std::cout << 1;
      std::cout << '\n';
    }
  }
  else {
    if (str[0] == '0') {
      std::cout << 1;
      for (int i = 0; i < (int)str.length() - 1; ++i) std::cout << 0;
      std::cout << '\n';
    }
    else {
      std::cout << 0;
      for (int i = 0; i < (int)str.length() - 1; ++i) std::cout << 1;
      std::cout << '\n';
    }
  }
  return 0;
}

I. Lie Detector

Description:

Andi is a young and prominent detective in the police force. His ability to track down criminals, uncover the truth, and solve cases never ceases to amaze all of his colleagues. One day, he is faced with a suspicious eyewitness testimony when working on a certain case. In usual cases, Andi simply ignores such unreliable testimony; however, in this case, the eyewitness testimony is too important to be ignored. To resolve this situation, Andi has to rely on technology, i.e. using a lie detector.
Andi proceeds to use a lie detector to detect whether the eyewitness testimony is true. However, Andi notices that the lie detector he used might have been tampered, thus, he employs a second lie detector to detect whether the first lie detector’s result is correct. This situation happens repeatedly such that Andi ends up employing $N$ lie detectors in total. The $i^{th}$ lie detector reports the truth of the $(i-1{)}^{th}$ lie detector for $i=2..N$, and the $1^{st}$ lie detector reports the truth of the eyewitness testimony.
In the end, Andi knows that the last ($N^{th}$) lie detector has not been tampered and always report the truth correctly. Now, he needs to determine whether the eyewitness testimony is true given the result of all lie detectors.
For example, let $N=4$ and the lie detectors result are $(\text{LIE},\text{LIE},\text{TRUTH},\text{TRUTH})$.

• The $4^{th}$ lie detector reports that the $3^{rd}$ lie detector is TRUTH. As the $4^{th}$ lie detector always report the truth correctly, then the $3^{rd}$ lie detector’s result is correct as it is.
• The $3^{rd}$ lie detector reports that the $2^{nd}$ lie detector is TRUTH. As the $3^{rd}$ lie detector’s result is correct as it is, then the $2^{nd}$ lie detector’s result is also correct as it is.
• The $2^{nd}$ lie detector reports that the $1^{st}$ lie detector is LIE. As the $2^{nd}$ lie detector’s result is correct as it is, then the $1^{st}$ lie detector’s result is wrong.
• The $1^{st}$ lie detector reports that the eyewitness testimony is LIE. As the $1^{st}$ lie detector’s result is wrong, then the eyewitness testimony is correct; in other words, what the eyewitness says is true.

Therefore, the eyewitness testimony in this example is true.

Input:

Input begins with a line containing an integer $N$ ($2\le N\le 100000$). The next $N$ lines, each contains a string $S_i$ (either TRUTH or LIE) representing the output of the $i^{th}$ lie detector for $i=1..N$ respectively.

Output

Output contains a string TRUTH or LIE in a line whether the eyewitness testimony is true or false.

Sample Input:

4
LIE
LIE
TRUTH
TRUTH

Sample Output:

TRUTH

Sample Input:

3
LIE
LIE
LIE

Sample Output:

LIE

题目链接

每个人给出上一个人发言的真假判断（最后一个人发言为真），求目击者的真假性（第一个人对其的判断）

倒推判断即可

AC代码:

#include 

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0); std::cout.tie(0);
  int n; std::cin >> n;
  std::vector<std::string> arr(n);
  for (auto &str : arr) std::cin >> str;
  std::reverse(arr.begin(), arr.end());
  bool flag = true;
  for (auto &it : arr) {
    if (it == "LIE") flag = !flag;
  }
  if (flag) std::cout << "TRUTH" << '\n';
  else std::cout << "LIE" << '\n';
  return 0;
}

K. Boomerangs

Description:

Let $G=(V,E)$ be a simple undirected graph with $N$ vertices and $M$ edges, where $V=\{1,\dots ,N\}$. A tuple $⟨u,v,w⟩$ is called as boomerang in $G$ if and only if $\{(u,v),(v,w)\}\subseteq E$ and $u̸=w$; in other words, a boomerang consists of two edges which share a common vertex.
Given $G$, your task is to find as many disjoint boomerangs as possible in $G$. A set $S$ contains disjoint boomerangs if and only if each edge in $G$ only appears at most once (in one boomerang) in $S$. You may output any valid disjoint boomerangs, but the number of disjoint boomerangs should be maximum.
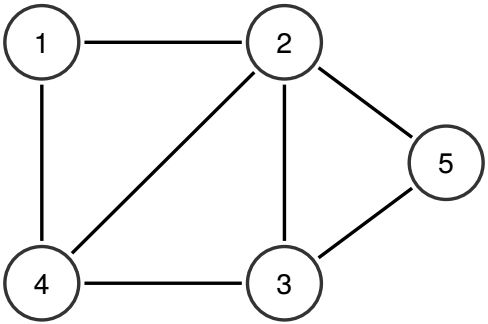
For example, consider a graph $G=(V,E)$ of $N=5$ vertices and $M=7$ edges where $E=\{(1,2)$, $(1,4)$, $(2,3)$, $(2,4)$, $(2,5)$, $(3,4)$, $(3,5)\}$.

The maximum number of disjoint boomerangs in this example graph is $3$. One example set containing the $3$ disjoint boomerangs is $\{⟨4,1,2⟩,⟨4,3,2⟩,⟨2,5,3⟩\}$; no set can contain more than $3$ disjoint boomerangs in this example.

Input:

Input begins with a line containing two integers: $N$ $M$ ($1\le N,M\le 100000$), representing the number of vertices and the number edges in $G$, respectively. The next $M$ lines, each contains two integers: $u_i$ $v_i$ ($1\le u_i<v_i\le N$), representing the edge $(u_i,v_i)$ in $G$. You may safely assume that each edge appears at most once in the given list.

Output

The first line of output contains an integer: $K$, representing the maximum number of disjoint boomerangs in $G$. The next $K$ lines, each contains three integers: $u$ $v$ $w$ (each separated by a single space), representing a boomerang $⟨u,v,w⟩$. All boomerangs in the output should be disjoint. If there is more than one valid solution, you can output any of them.

Sample Input:

5 7
1 2
1 4
2 3
2 4
2 5
3 4
3 5

Sample Output:

3
4 1 2
4 3 2
2 5 3

Sample Input:

4 6
1 2
1 3
1 4
2 3
2 4
3 4

Sample Output:

3
1 2 3
1 3 4
1 4 2

Sample Input:

3 3
1 2
1 3
2 3

Sample Output:

1
2 1 3

题目链接

求无向图中三元组（两边公用一顶点）的最大数量及其方案

对每个连通块进行深搜并分配边即可

AC代码:

#include 

int n, m;
std::vector<std::vector<int>> g;
std::vector<bool> vis;
int tot;
std::vector<int> cnt;
struct tuple {int u, v, w;};
std::vector<tuple> ans;

bool Dfs(int cur, int pre = -1) {
  cnt[cur] = ++tot;
  vis[cur] = true;
  int v = -1;
  for (auto it : g[cur]) {
    if (it == pre) continue;
    if (vis[it]) {
      if (cnt[it] > cnt[cur]) continue;
      if (v == -1) v = it;
      else {
        ans.emplace_back((tuple){v, cur, it});
        v = -1;
      }
    }
    else {
      if (Dfs(it, cur)) {
        if (v == -1) v = it;
        else {
          ans.emplace_back((tuple){v, cur, it});
          v = -1;
        }
      }
    }
  }
  if (v == -1) return true;
  else if (pre != -1) ans.emplace_back((tuple){v, cur, pre});
  return false;
}

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0); std::cout.tie(0);

  std::cin >> n >> m;
  g.resize(n);
  vis.assign(n, false); cnt.assign(n, 0);
  for (int i = 0, u, v; i < m; ++i) {
    std::cin >> u >> v;
    --u; --v;
    g[u].emplace_back(v);
    g[v].emplace_back(u);
  }

  for (int i = 0; i < n; ++i)
    if (!vis[i])
      Dfs(i);

  std::cout << ans.size() << '\n';
  for (auto &it : ans) std::cout << it.u + 1 << " " << it.v + 1 << " " << it.w + 1 << '\n';
  return 0;
}

L. Binary String

Description:

A binary string is a non-empty sequence of $0$'s and $1$'s, e.g., 010110, 1, 11101, etc. Ayu has a favorite binary string $S$ which contains no leading zeroes. She wants to convert $S$ into its decimal representation with her calculator.
Unfortunately, her calculator cannot work on any integer larger than $K$ and it will crash. Therefore, Ayu may need to remove zero or more bits from $S$ while maintaining the order of the remaining bits such that its decimal representation is no larger than $K$. The resulting binary string also must not contain any leading zeroes.
Your task is to help Ayu to determine the minimum number of bits to be removed from $S$ to satisfy Ayu’s need.
For example, let $S$ = 1100101 and $K=13$. Note that 1100101 is $101$ in decimal representation, thus, we need to remove several bits from $S$ to make it no larger than $K$. We can remove the $3^{rd}$, $5^{th}$, and $6^{th}$ most significant bits, i.e. 1100101 $\to$ 1101. The decimal representation of 1101 is $13$, which is no larger than $K=13$. In this example, we removed $3$ bits, and this is the minimum possible (If we remove only $2$ bits, then we will have a binary string of length $5$ bits; notice that any binary string of length $5$ bits has a value of at least $16$ in decimal representation).

Input:

Input begins with a line containing an integer $K$ ($1\le K\le 2^{60}$) representing the limit of Ayu’s calculator. The second line contains a binary string $S$ ($1\le |S|\le 60$) representing Ayu’s favorite binary string. You may safely assume $S$ contains no leading zeroes.

Output

Output contains an integer in a line representing the minimum number of bits to be removed from $S$.

Sample Input:

13
1100101

Sample Output:

3

Sample Input:

13
1111111

Sample Output:

4

题目链接

求将一个二进制数减小到 $K$ 的最少操作次数

通过找规律可发现将二进制减小的最多对0、1来说有两种情况

1. 1需删除最高位
2. 0需删除最低位

所以模拟比较删除即可

AC代码:

#include 
const long long inf = 1ll << 61;

std::vector<bool> vis;

long long Num(std::string str) {
  long long ans = 0, k = 0;
  for (long long i = str.length() - 1; i >= 0; --i) {
    if (vis[i] == false) continue;
    if (str[i] == '1') ans += 1ll << k;
    k++;
  }
  return ans;
}

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0); std::cout.tie(0);

  long long k; std::cin >> k;
  std::string str; std::cin >> str;
  std::vector<int> one_pos, zero_pos;
  for (int i = 1; i < (int)str.length(); ++i) {
    if (str[i] == '1') one_pos.emplace_back(i);
    else zero_pos.emplace_back(i);
  }

  vis.assign(str.size(), true);
  long long bit = Num(str), cnt = 0;
  while (bit > k) {
    long long v1 = inf, v2 = inf;
    if (!one_pos.empty()) {
      vis[one_pos[0]] = false;
      v1 = Num(str);
      vis[one_pos[0]] = true;
    }
    if (!zero_pos.empty()) {
      vis[zero_pos.back()] = false;
      v2 = Num(str);
      vis[zero_pos.back()] = true;
    }
    if (v1 < v2) {
      vis[one_pos[0]] = false;
      one_pos.erase(one_pos.begin());
      bit = v1;
    }
    else {
      vis[zero_pos.back()] = false;
      zero_pos.pop_back();
      bit = v2;
    }
    cnt++;
  }

  std::cout << cnt << '\n';
  return 0;
}