DetectoRS: Detecting Objects with Recursive Feature Pyramid and Switchable Atrous Convolution论文学习

Abstract

很多的目标检测器通过 looking and thinking twice 的方式实现了惊人的表现。本文作者针对目标检测主干网络的设计，研究了该机制。在宏观层面，作者提出了递归特征金字塔，将来自FPN的额外的反馈连接加入到自下而上的主干层。在微观层面，作者提出了可切换的空洞卷积（SAC），它以不同的空洞率（rate）对特征进行卷积，并使用switch函数合并卷积后的结果。这样就得到了DetectoRS，极大地提升了目标检测性能。在COCO 测试验证集上，DetectoRS 取得了SOTA的成绩，目标检测项为$54.7\%$的边框AP，实例分割项为$47.1\%$的mask AP，全景分割项为$49.6\%$的PQ。代码位于：https://github.com/joe-siyuan-qiao/DetectoRS。

1. Introduction

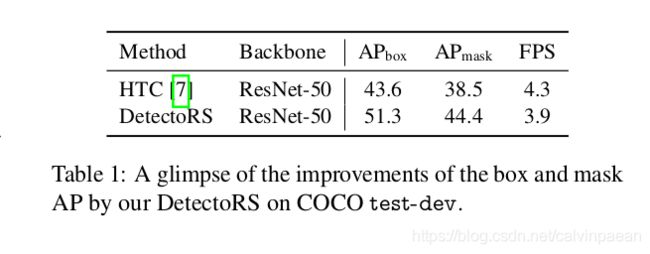
要想找到目标物体，人类的视觉感知会通过反馈连接来传入高层及的语义信息，选择性地增强或抑制神经元活动。受此启发，计算机视觉领域实践了 looking and thinking twice 的思想，取得了优异的表现。许多流行的双阶段检测器，如Faster R-CNN，首先基于区域特征，输出候选目标框。Cascade R-CNN 设计了一个多阶段的检测器，它使用更优质的样本来训练后面的检测器heads。该设计思想非常成功，促使我们去研究目标检测的主干网络如何设计。作者在宏观和微观两个层面实现了该机制，就是 DetectoRS，它极大地提升了SOTA目标检测器 HTC 的性能，推理速度没降，如表1所示。

在宏观层面，递归特征金字塔（RFP）构建于FPN之上，将FPN层中的额外反馈连接加入到自下而上的主干层中，如图1(a)所示。将递归结构拆开为一组顺序实现，我们得到了一个目标检测器的主干网络，它会关注图片至少两次。与Cascade R-CNN 中的级联检测器的heads类似，RFP递归地增强FPN，产生的特征表示越来越强。与Deeply-Supervised Nets相似，反馈连接可以将从检测器heads传来的梯度，传回自下而上的低层级主干网络中，加速训练并提升性能。RFP实现了looking and thinking twice的顺序设计，自下而上的主干网络和FPN可以多次运行，输出的特征取决于之前步骤的输出。

在微观层面，作者提出了可切换的空洞卷积（SAC），用不同的空洞率来对相同的输入特征做卷积，使用switch函数来结合结果。图1b 展示了 SAC 的概念。Switch函数在空间上互相依赖，即特征图的每个位置有着不同的switches来控制SAC的输出。在检测器中，作者将自下而上的主干网络中所有$3\times 3$标准卷积层替换为SAC，显著地提升了检测器性能。[39,74]也采用了条件卷积，将不同的卷积结果结合为一个输出。与这些方法不同，这些架构需要从头开始训练，而SAC提供了一个机制，可以很容易地转化预训练的标准卷积网络（如ImageNet-预训练权重）。而且SAC中使用了一个新的权重闭锁机制，除了一个可训练的差异之外，不同空洞卷积的权重是一样的。

将RFP和SAC的结合起来，就有了DetectoRS。为了证明其有效性，作者将DetectoRS加入到SOTA的HTC中，在COCO数据集上做实验。在COCO测试验证集上，作者报告了目标检测的边框AP、实例分割的mask AP，和全景分割的PQ。用ResNet-50作为主干网络的DetectoRS将HTC的边框AP提升了$7.7\%$，mask AP提升了$5.9\%$。此外，将DetectoRS结合到ResNeXt-101-32x4d中，取得了$54.7\%$的边框AP和$47.1\%$的mask AP。DetectoRS 搭配 DeepLabV3+和Wide-ResNet-41作为主干网络，在全景分割任务上取得了$49.6\%$的PQ，是一个新的记录。

2. Related Works

目标检测。目标检测方法主要有2类：单阶段方法和多阶段方法。多阶段检测器通常更加灵活、准确，但是比起单阶段方法来说更加复杂。本文作者用多阶段的HTC作为基线模型。

多层级特征。递归特征金字塔基于FPN而来，FPN 利用多尺度特征来进行有效的目标检测。之前，许多目标检测器直接使用主干网络的多尺度特征，而FPN加入了自上而下的path，将不同尺度的特征按照顺序进行结合。PANet 在FPN之上，增加了另一个自下而上的path。STDL通过尺度转换模块来利用跨尺度的特征。G-FRNet 通过gating units增加反馈信息。NAS-FPN和Auto-FPN使用神经结构搜索找到最佳的FPN结构。EfficientDet提出复用一个简单的BiFPN层。与它们不同，本文的递归特征金字塔重复连入自下而上的主干网络，增强FPN特征表示的能力。此外，作者在FPN中加入了空洞空间金字塔池化（ASPP），增强特征，与Seamless 的 mini-DeepLab设计相似。

递归卷积网络。人们提出了许多递归方法，解决不同类型的计算机视觉问题。最近有一个递归方法CBNet用于目标检测，将多个主干网络级联起来，它输出的特征作为FPN的输入。相反，本文的RFP通过ASPP加持的FPN来执行递归计算。

条件卷积。条件卷积网络采用动态卷积核、宽度或深度。与它们不同，本文的可切换空洞卷积（SAC）不会改变预训练模型，将标准卷积转换为条件卷积。SAC因此对于许多预训练主干网络来说，可以即插即用。而且，SAC使用全局上下文信息，以及一个创新的权重闭锁机制，来让它更加有效。

3. 递归特征金字塔

3.1 特征金字塔网络

这一部分将介绍下特征金字塔网络。$B_i$表示自下而上主干网络的第$i$个阶段，$F_i$表示第$i$个自上而下FPN操作。搭配FPN的主干网络输出一组特征图$\{f_i|i=1,...,S\}$，其中$S$是阶段的个数。例如图2a中，$S=3$。$\forall i=1,...,S$，输出特征$f_i$定义为：

$$f_i=F_i(f_{i+1},x_i),x_i=B_i(x_{i-1})$$

其中$x_0$是输入图像，$f_{S+1}=0$。目标检测器构建于FPN之上，使用$f_i$用于检测计算。

3.2 递归特征金字塔

RFP往FPN中增加了反馈连接，如图2b所示。在将它们连接回自下而上的主干网络前，我们用$R_i$表示特征变换，在将它们连接到自下而上的主干网络之前。然后，对于$\forall i=1,...,S$，输出特征$f_i$的定义为：

$$f_i=F_i(f_{i+1},x_i),x_i=B_i(x_{i-1},R_i(f_i))$$

这样RFP就是递归操作了。我们将它拆开为一个网络序列，即 $\forall i=1,...,S,t=1,...,T$：

$$f_i^t=F_i^t(f_{i+1}^t,x_i^t),x_i^t=B_i^t(x_{i-1}^t,R_i^t(f_i^{t-1}))$$

其中$T$为拆开的次数，我们用上标$t$来表示第$t$步的运算与特征。$f_i^0$被设为0。在实现中，$F_i^t$和$R_i^t$在不同的步骤中共享。在第5部分的实验研究中，作者列出了共享的和不同的$B_i^t$，以及不同$T$的表现。在实验中，作者使用了不同的$B_i^t$，设$T=2$。

作者改进了ResNet主干网络$B$，将$x$和$R(f)$作为输入。ResNet有4个阶段，每个都由多个相似的模块构成。作者只改变了每个阶段的第一个模块，如图3所示。该模块计算一个3层的特征，将它加到shortcut计算出的特征上。为了使用特征$R(f)$，作者增加了另一个卷积层，卷积核大小是1。该层的权重初始化为0，确保加载预训练权重时，它不会有任何的影响。

作者使用空洞空间金字塔池化（ASPP）来实现连接模块$R$，它将特征$f_i^t$作为输入，将之变换为RFP特征，如图3所示。在该模块中，有4个平行的分支，将$f_i^t$作为输入，输出然后沿着通道维度进行concat，得到最终的输出$R$。它们中的三条分支使用一个卷积层和一个ReLU层，输出通道数是输入通道数的$1/4$。最后一个分支使用全局平均池化层来压缩特征，后面跟着一个$1\times 1$卷积层和一个ReLU层，将压缩后的特征变换为$1/4$大小（通道维度）的特征。最后，我们将这些特征重新缩放，与其它三个分支的特征进行concat。这三个分支里的卷积层的配置如下：卷积核大小为$[1,3,3]$，空洞率为$[1,3,6]$，padding为$[0,3,6]$。与原始的ASPP不同，作者并没有在concat特征之后跟着一个卷积层，因为$R$没有输出最终的结果。注意，这四个分支中的每一个所输出的特征，其维度都是输入特征的$1/4$，将它们concat之后就会得到一个与输入特征$R$一样大小的特征。在第5部分，作者证明了有和没有ASPP模块时RFP的性能。

3.4 Output updated by the fusion module

如图2c所示，RFP额外地使用了融合模块，将$f_i^t$和$f_i^{t+1}$结合起来，更新上面等式中第$t+1$个阶段的$f_i$值。该融合模块与递归神经网络中的更新过程非常相似，如果我们将$f_i^t$看作为一个数据序列。在第2到第$T$步骤中，使用了融合模块。在第$t+1$（$t=1,...,T-1$）的步骤中，融合模块将第$t$步的特征$f_i^t$与FPN在第$t+1$步中最新计算出的特征$f_i^{t+1}$作为输入。该融合模块使用特征$f_i^{t+1}$来计算注意力图，通过一个卷积层和一个sigmoid操作。该注意力图用于计算$f_i^t$和$f_i^{t+1}$的加权和，来更新$f_i$。这个$f_i$将作为$f_i^{t+1}$，在后续的步骤中使用。

4. 可切换的空洞卷积

4.1 空洞卷积

空洞卷积是增大卷积层滤波器感受野的有效方式。特别地，空洞率$r$的空洞卷积在两个连续的滤波器值之间引入$r-1$个0，相当于将卷积核大小由$k\times k$增大到$k_e=k+(k-1)(r-1)$，而不会增加参数的个数或计算量。图1b为$3\times 3$卷积层和空洞率为1（红色）与2（绿色）的一个例子：不同尺度的同类物体可以通过相同的卷积权重和不同的空洞率来检测。

4.2 可切换的空洞卷积

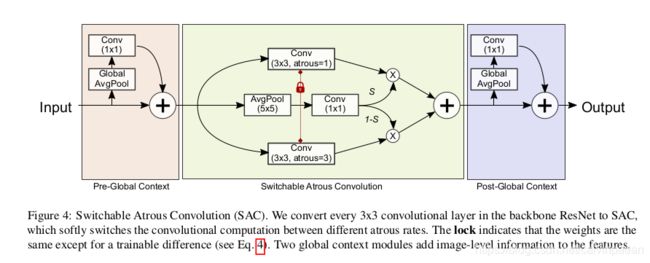
作者介绍了SAC的细节。图4展示了SAC的整体结构，它主要有3个组成：2个全局上下文模块分别加在SAC组建的前面和后面。这部分关注在SAC中间的主要构成上，随后作者会介绍全局上下文模块。

作者用$y=\text{Conv}(x,w,r)$来表示卷积操作，权重为$w$，空洞率为$r$，输入是$x$，输出是$y$。然后，将卷积层转化为一个SAC：

$$\text{Conv}(x,w,1)\underset{\text{to SAC}}{\overset{\text{Convert}}{}}S(x)\cdot \text{Conv}(x,w,1)+(1-S(x))\cdot \text{Conv}(x,w+\Delta w,r)$$

其中$r$是SAC的超参数，$\Delta w$是可训练的权重，switch函数$S(\cdot )$用一个$5\times 5$的核的平均池化层，后面跟着一个$1\times 1$的卷积层，如图4所示。该swtich函数依赖于输入和位置；因此，主干网络模型能够适应不同的尺度。实验中作者设$r=3$。

作者提出了一个闭锁机制，设一个权重为$w$，其它的为$w+\Delta w$。目标检测器通常用预训练权重来初始化网络。但是，对于一个由标准卷积转化而来的SAC层，没有较大空洞率的权重。由于不同尺度的物体大概都可以用相同的权重，而空洞率不同来检测到，很自然地我们就可以用预训练模型的权重来初始化这些缺失的权重。本文实现将$w+\Delta w$用作为这些缺失的权重，其中$w$来自于预训练权重，而$\Delta w$初始化为0。当$\Delta w=0$时，发现AP降低了$0.1\%$。但是不用闭锁机制的话，AP会下降许多。

4.3 全局上下文

如图4所示，作者在SAC前后共插入了2个全局上下文模块。这2个模块都很轻量级，输入特征首先通过一个全局平均池化层压缩。全局上下文模块与SENet类似，除了2个不同之处：(1) 我们只有一个卷积层，没有非线性层；(2) 输出被加到主干之后，而不是通过sigmoid计算出的值来乘到输入上。作者发现将全局上下文信息加到SAC之前（即将全局信息加到switch函数里），对检测效果有正面的作用。作者猜测，这是因为$S$在有全局信息的时候，所做出的预测更加稳定。然后，作者将全局信息移除switch函数，将它放在主干部分的前面和后面，这样$Conv$和$S$都会受益。作者没有采用原始的SENet方式，因为没有发现它对最终的AP有何影响。

4.4 实现细节

在实现中，作者使用了变形卷积来代替等式4中的卷积操作。它们的offset函数没有共享。第5部分会讲述SAC有和没有变形卷积时的性能比较。作者在ResNet和其变体上采用SAC，在主干网络中将所有的$3\times 3$卷积替换。全局上下文模块的权重和偏置都被初始化为0。swtich $S$中的权重初始化为0，偏置初始化为1。$\Delta w$初始化为0。上述初始化策略确保了，当我们加载从ImageNet上训练得到的预训练模型时，将所有$3\times 3$卷积转化为SAC不会改变输出。

4. Experiments

Pls read paper for more details.