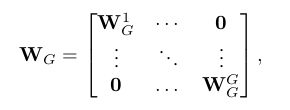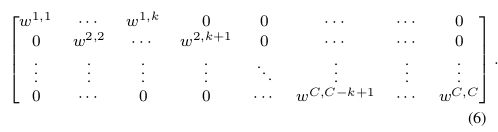ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 论文学习

Abstract

通道注意力机制被证明可以极大地提升CNN的表现。但是，现有的方法都致力于设计出更复杂的注意力模块，来实现更高的准确率，不可避免地增加模型的复杂度。为了克服表现与复杂度之间的trade-off，作者提出了一个高效的通道注意力（ECA）模块，只用少量的参数，却能带来明显的性能提升。通过分析SENet中的通道注意力模块，作者证明保持维度对于学习通道注意力非常重要，合适的跨通道交流可以保持性能，而极大地降低复杂度。因此，本文提出了一个局部跨通道交流策略，不需要降维，可以通过1D卷积高效率地实现。而且，作者设计了一个方法，可以动态地选择1D卷积的卷积核大小，决定局部跨通道交流的覆盖范围。ECA模块非常高效管用，比如本文模块与 ResNet-50主干网络相比，其参数量和计算量分别是80 vs. 24.37M，$4.7e-4$ GLOPs vs. $3.86$ GFLOPs，而且其top-1准确率得到了$2\%$的提升。作者在图像分类、目标检测、实例分割任务上进行了评测，利用ResNets和MobileNetV2主干网络。实验结果显示，该模块更加高效率，而性能优异。

1. Introduction

CNN 被广泛使用在计算机视觉领域，在很多任务上都取得了突破，如图像分类、目标检测和实例分割。自从AlexNet，该领域的许多研究都在不断地提升了CNN的性能。最近，在卷积模块中加入通道注意力机制得到了许多的关注，取得了巨大的性能提升。Squeeze-and-excitation网络是其中具有代表性的，它学习每个卷积模块的通道注意力机制，给深度CNN结构带来显著的性能提升。

依照SENet中的 squeeze(如特征聚合)和 excitation(如特征重校准)操作，一些方法通过学习复杂的通道间依赖关系，或者结合额外的空间注意力机制，来改进SE模块。尽管这些方法都取得了更高的准确率，但是会增加模型复杂度和计算负担。与这些方法不同，本文关注于一个问题：能否以更高效的方式来学习通道注意力？

为了回答这个问题，作者首先回顾了SENet的通道注意力模块。给定输入特征，SE模块首先对每个通道单独地使用一个全局平均池化，然后跟着2个全连接层和非线性激活函数来生成通道的权重。这2个全连接层用于获取非线性跨通道的交流，降维来控制模型复杂度。尽管这个策略被广泛应用在随后的通道注意力模块中，本文的研究发现降维会给通道注意力预测带来副作用，获取所有通道的依赖关系是低效且没必要的。

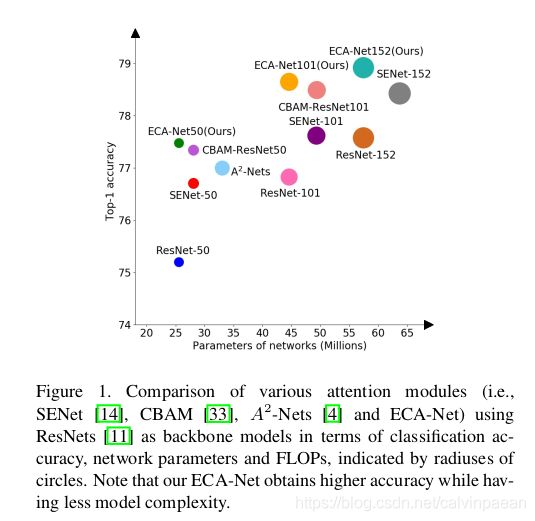
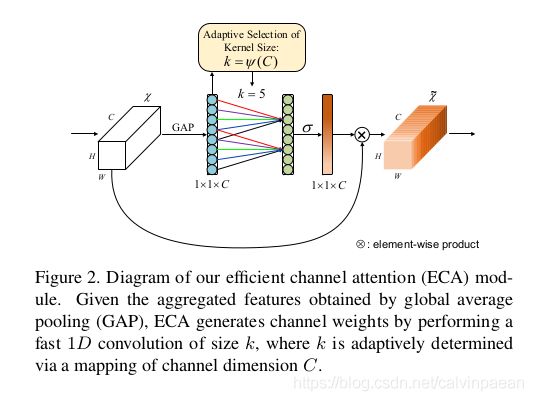
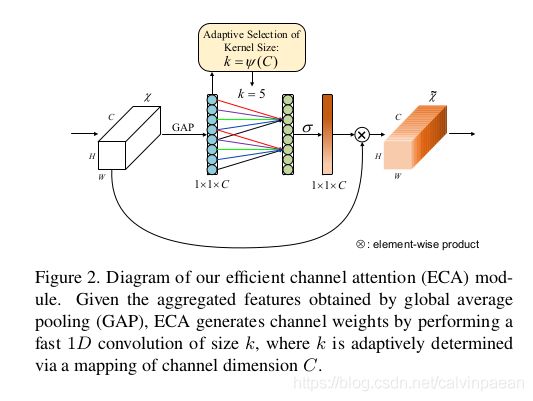
因此，本文提出了ECA模块，避免降维，以高效率的方式来实现跨通道交流。如图2所示，在没有降维的通道全局平均池化后，ECA会使用每个通道及其$k$个近邻，来实现局部跨通道交流。该方法效率高且有效。ECA可以通过快速1D卷积来高效实现，该卷积核大小是$k$，$k$代表了局部跨通道交流的覆盖范围，如会有多少个近邻参与到单个通道的注意力预测中去。为了避免通过cross-validation来手动调节$k$，交流的覆盖范围（如卷积核大小$k$）与通道维度成比例关系。如图1和表3所示，与主干网络相比，使用了ECA模块的CNN（ECA-Net）会引入极少的参数与计算量，但带来的增益很明显。例如，ResNet-50有24.37M个参数，计算量是3.86 GLOPs，ECA-Net50的参数量则只有80个，计算量是$4.7e-4$GLOPs。同时，ECA-Net50要比ResNet-50的准确率高$2.28\%$。

表1总结了现有注意力模块，关于通道是否降维、跨通道交流和轻量级模型，我们可以看到ECA模块能够学到有效的通道注意力，无需降维操作，以极为轻量的方式来实现跨通道交流。为了评价该方法，作者在ImageNet-1K和MS COCO数据集上做了大量的实验。

本文总结如下。(1) 作者分析了SE模块，证明无需降维操作，恰当的跨通道交流对于学习有效的通道注意力非常重要。(2) 基于上述分析，作者尝试设计一个极为轻量的通道注意力模块，提出了高效通道注意力ECA模块，不会增加模型复杂度，但能带来明显提升。(3) 在ImageNet-1K和MS COCO上的实验结果显示，该方法的模型复杂度较低，但是表现优于现有SOTA方法。

2. Related Work

注意力机制已被证明可以提高CNN的性能。SE-Net 第一次提出了一个有效的方式来学习通道注意力，并取得不错的表现。随后，注意力模块的发展可以分为2个方向：(1) 特征融合增强；(2) 通道和空间注意力结合。CBAM 使用了平均和最大池化来融合特征。GSoP 引入了二阶池化，更有效地融合特征。GE 则使用深度卷积探索了空间扩展性，融合特征。CBAM 和 scSE 使用一个2D卷积来计算空间注意力，卷积核大小是$k\times k$，然后将之与通道注意力结合。与Non-Local 有着相似的思想，GC-Net 设计了一个简单的NL网络，并与SE模块整合，得到一个轻量级的模块，从而对长期依赖关系建模。Double Attention Networks($A^2$-Nets)为NL模块引入了一个新的关系函数，用于图像或视频识别。Dual Attention Network(DAN) 在语义分割上，同时考虑了NL-based通道注意力和空间注意力。但是，大多数NL-based注意力模块只能用在单个或少量的卷积模块中，因为它们的复杂度很高。显然，上述所有的方法都关注在如何设计更复杂的注意力模块，来取得更高的性能。与它们不同，ECA 旨在学习有效的通道注意力，而复杂度很低。

本文与高效卷积相关，可用于构建轻量级CNN。两个广泛应用的高效率卷积就是分组卷积和深度可分离卷积。如表2所示，尽管这些卷积的参数都不多，但是在注意力模块上的功效却很低。ECA模块意图获取局部跨通道交流，与通道局部卷积和通道卷积有相似性；与它们不同，ECA通过自适应的卷积核大小来调节1D卷积，在通道注意力模块中代替全连接层。与分组和深度可分离卷积相比，本文方法得到了更优的表现，而复杂度更低。

3. Proposed Method

本部分，作者首先回顾了SENet中的通道注意力模块。然后，通过研究降维和跨通道交流的作用，经验性分析了SE模块。这就促使了作者提出ECA模块。此外，作者提出了一个方法来动态地决定ECA的参数，并将之应用到CNN中去。

3.1 Revisiting Channel Attention in SE Block

将卷积模块的输出记作$\chi \in {\mathbb{R}}^{W\times H\times C}$，其中$W,H,C$分别是宽度、高度、通道维度（滤波器个数）。因此，SE模块的通道权重可以计算为：

$$\omega =\sigma (f_{\{W_1,W_2\}}(g(\chi )))$$

其中，$g(\chi )=\frac{1}{WH}{\sum }_{i=1,j=1}^{W,H}{\chi }_{ij}$是通道全局平均池化（GAP），$\sigma$是Sigmoid函数。令$y=g(\chi ),f_{\{W_1,W_2\}}$表示如下：

$$f_{\{W_1,W_2\}}(y)=W_{2}ReLU(W_{1}y)$$

其中ReLU就是Rectified Linear Unit函数。为了不让复杂度很高，$W_1,W_2$的大小被设定为$C\times (\frac{C}{r})$和$(\frac{C}{r})\times C$。可以看到$f_{\{W_1,W_2\}}$包含了通道注意力模块的所有参数。尽管上面等式中的降维操作可以降低复杂度，但是摧毁了通道和权重之间直接的对应关系。例如，单个全连接层通过各通道的线性组合，可预测每个通道的权重。但是上面等式2首先将通道特征映射到一个低维度空间，然后再映射回来，使得通道并不直接对应着权重。

3.2 Efficient Channel Attention Module

回顾完SE模块，作者比较分析了通道降维和通道注意力学习过程中跨通道交流的作用。根据这些分析，作者提出了ECA模块。

3.2.1 Avoiding Dimensionality Reduction

等式2中的降维操作使得通道和权重并不直接对应。为了验证，作者将原始的SE模块和其变体（SE-Var1, SE-Var2, SE-Var3）做了比较，它们都没有做降维。如表2所示，SE-Var1 没有参数，仍然优于原始的SE网络，表明通道注意力可以提升CNN的性能。同时，SE-Var2 独立地学习每个通道的权重，要优于SE模块，而参数要更少。这就表明，通道和其权重之间需要建立直接的对应关系，不降维要比使用非线性通道依赖更加重要。此外，SE-Var3使用单个全连接层，效果要比SE模块中降维了的2个全连接层好。上述结果清楚地证明，不降维对于学习通道注意力很有帮助。因此，作者设计了ECA模块，没有用到降维。

3.2.2 Local Cross-Channel Interation

给定没有降维的聚合特征$y\in {\mathbb{R}}^C$，通道注意力可以通过下面等式来学习：

$$\omega =\sigma (Wy)$$

其中$W$是一个$C\times C$的参数矩阵。对于SE-Var2和SE-Var3，我们有

其中，SE-Var2 的 $W_{var2}$是一个对角矩阵，包含$C$个参数；SE-Var3的$W_{var3}$是一个全矩阵，包含$C\times C$个参数。如上面等式，其核心区别是，SE-Var3考虑跨通道交流，而SE-Var2则不会，因此SE-Var3的表现要更好。该结果表明，跨通道交流对于通道注意力学习有帮助。但是，SE-Var3 需要大量的参数，导致模型复杂度高，尤其是通道数很多的时候。

在SE-Var2和SE-Var3之间，一个折中方案就是将$W_{var2}$替换为一个块对角矩阵，即

它将通道分为$G$个组，每个包含$C/G$个通道，在每个组内独立地学习通道注意力，在局部范围内实现跨通道交流。因而，它涉及到了$C^2/G$个参数。从卷积的角度来看，SE-Var2、SE-Var3和上面等式可以分别看作为深度可分离卷积、全连接层和带分组卷积的全连接层。带分组卷积的SE模块（SE-GC）表示为$\sigma (G{C}_G(y))=\sigma (W_{G}y)$。但是，过度使用分组卷积会增加内存读写成本，降低计算效率。而且如表2所示，不同组数的SE-GC并不会给SE-Var2带来增益，表明它对于实现局部跨通道交流没什么用。原因可能是，SE-GC完全丢失了不同分组内的依赖关系。

本文，作者探索了另一个实现局部跨通道交流的方法，确保其有效性。作者使用矩阵$W_k$来学习通道注意力，

$W_k$有$k\times C$个参数，要少于等式5。而且，它避免了等式5中各分组完全独立的问题。如表2所示，等式6（ECA-NS）的方法超过了等式5的SE-GC。对于等式6，$y_i$的权重可以仅考虑$y_i$和其$k$个近邻的交流，

$${\omega }_i=\sigma (\sum _{j=1}^k{w}_i^j{y}_i^j),y_i^j\in {\Omega }_i^k$$

其中${\Omega }_i^k$表示$y_i$的$k$个毗邻的通道集合。

一个更有效的方式就是，所有的通道共享学习参数：

$${\omega }_i=\sigma (\sum _{j=1}^k{w}^j{y}_i^j),y_i^j\in {\Omega }_i^k$$

注意该策略可以很容易地通过快速1D卷积实现，卷积核大小是$k$，

$$\omega =\sigma (C1D_k(y))$$

其中$C1D$表示1D卷积。这里，等式9中的方法叫做ECA模块，只有$k$个参数。如表2所示，$k=3$的ECA模块可以取得与SE-Var3相似的结果，但是复杂度要低非常多，确保了其效率和有效性，实现局部跨通道交流。

3.2.3 Coverage of Local Cross-Channel Interation

因为ECA模块意图实现局部跨通道交流，所以我们要决定其交流的覆盖范围（如1D卷积的卷积核大小$k$）。在不同的CNN结构中，对于不同通道数量的卷积模块，我们可以手动去调节最优的交流覆盖范围。但是，通过cross-validation来手动调会消耗大量的算力资源。分组卷积在CNN结构使用中很成功，可以提升CNN的性能，给定固定个数的分组，高维（低维）通道会出现长期（短期）卷积。有着相似的思想，交流的覆盖范围与通道维度$C$成比例关系，就是合理的。换句话说，在$k$和$C$之间存在着映射$\varphi$:

$$C=\varphi (k)$$

最简单的映射就是线性函数，$\varphi (k)=\gamma \ast k-b$。但是，线性函数的关系太局限了。另一方面，我们知道通道维度$C$(滤波器个数)通常是$2$的指数。因此，作者将线性函数$\varphi (k)=\gamma \ast k-b$扩展为非线性函数：

$$C=\varphi (k)=2^{\gamma \ast k-b}$$

然后，给定通道维度$C$，卷积核大小$k$可以自适应地决定：

$$k=\psi (C)=|\frac{{\log }_2(C)}{\gamma }+\frac{b}{\gamma }{|}_{odd}$$

其中$|t{|}_{odd}$表示$t$最近的奇数个邻居。本文，$\gamma$设为2,$b$设为1。很清楚，对于映射$\psi$，通过非线性映射，高维通道有着更长期的交流，而低维通道的交流要短一些。

3.3 ECA Module for Deep CNNs

图2 显示了ECA模块。用GAP聚合完卷积特征后，没有降维，ECA模块首先自适应地判断卷积核大小$k$，然后执行1D卷积，后面跟着一个Sigmoid函数来学习通道注意力。为了将ECA应用在CNN上，作者将SE模块替换为ECA模块。该网络被叫做ECA-Net。图3给出了ECA的PyTorch代码。

4. Experiments

Pls read paper for more details.