深度优先搜索和广度优先搜索C语言 (紫皮书)
源代码在文章最后!
深度优先搜索
深度优先搜索又叫depth first search,是一种在开发爬虫早期比较常用的方法,这里我会用最易懂的方法让大家理解深度优先搜索**,所谓深度优先搜索,就是找到图中的一个节点,然后依此寻找与他相关的下一个节点,形象地来说就是一条路走到黑**,
而广度优先搜索就是以一个节点开头,一次访问这个节点所有有关系的节点,先横向发展,在纵向延伸。需要用图举一个例子

这是一个无向图,现在要对这个无向图进行深度优先搜索。如果我们把1当作开头的节点,那么可能的寻找顺序为1->2->5->3是深度优先搜索的一条路,
想要对一个图进行深度优先搜索,就先要想办法将这个图存储起来,这里我们选择用邻接矩阵进行储存,我用的邻接矩阵是int类型的,也可以自己定义结构体来储存更多信息。
邻接矩阵是这样表现这个图的。
第几行就是第几个节点**(从0开始)**,在一行中,哪一列的值为1,就是说明行所代表的节点与列所代表的节点有关系。
int graph[][6] = { 0,1,1,1,0,0,
1,0,0,0,1,0,
1,0,0,0,1,0,
1,0,0,0,0,1,
0,1,1,0,0,0,
0,0,0,1,0,0, };
//创立无向图
这里可以看到这个图是沿对角线对称的,这也是无向图的特点,这个无向图总共有六个元素,就是上面图中所画的图。
要分清楚这个图中的节点是否被访问过,我们还需要一个数组visited[]来记录每个节点的访问信息。
在判断这个图中的节点是不是每一个都被访问了,我们只需要遍历visited数组,如果数组中的所有值都是1(被访问过了),那么就可以结束搜索。
下面是广度优先搜索的代码
void DFS(int graph[][6],int v,int visited[])//参数分别是图,开始搜索的节点,visited数组
{
printf("访问%d节点\n",v);//可以看到访问节点的顺序
visited[v] = 1;//表示被访问过
for(int w = 0;w < VexNum;w++)//寻找第v行所有没有被访问过的节点
{
if(graph[v][w] != 0&&!visited[w])//在一行中搜索没有被访问过的节点
{
DFS(graph,w,visited);//以这个节点为基础开始访问
}
}
}
从这个图中就可以感受到 “一条路走到黑的特点” ,找到一个节点,标记访问之后,紧接着寻找与他有关的下一个节点,而不是遍历所有与他相关的节点,所以深度优先搜索更容易到达数据的最低端。时间复杂度是O(n+e),n是节点数,e是边数
广度优先搜索
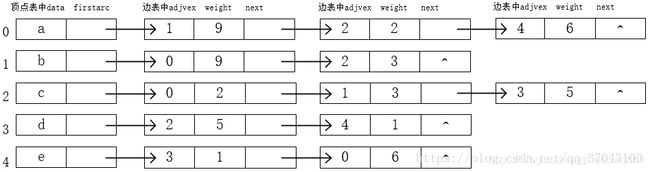
下面是有关广度优先搜索的内容,和深度优先搜索结合起来会更加易懂。为了方便描述和理解,这里用邻接表而不是邻接矩阵来储存图之间的关系。邻接表和邻接矩阵就不做过多介绍了。
大家如果对邻接表有疑问,最好先搞清楚邻接表,不然下面的内容可能会有理解问题。
typedef struct ArcNode{//边节点的数据结构
int loc;//边的一个端点,
struct ArcNode* nextarc;//指向与第一个图节点有关的下一个图节点
}ArcNode;
typedef struct{//图中每一个节点的数据结构
int data;//节点所代表的权值
ArcNode* firstarc;//指向该结点的第一个边界点
}VNode;
其中VNode是图中的节点,ArcNode是与VNode有关系的节点,虽然也代表了图中的节点,和VNode有区别,只是用来表示节点之间的关系。
在输入节点之间的关系的时候,使用头插法比较简便,不需要向后找到链表的末尾,
其中ArcNum是图中边的总数。
插入的方法具体是:
1.获取两个有关系的节点loc1,loc2
2.将loc2打包成一个边节点,
3.因为loc1和loc2有联系,找到loc1所代表的节点,然后将loc2打包后的节点插入loc1所代表的节点和loc1的firstArc之间,就是让loc2成为loc1的firstArc,loc1的节点往后依此移动一位,
4.因为建立的是无向图,所以要对loc2所代表的图节点与loc1在建立一次关系。
for(int i = 0;i < ArcNum;i++)//获取节点之间边的关系
{
int loc1,loc2;
scanf("%d%d",&loc1,&loc2);//输入两个相关的节点
loc1--;//从零开始计算
loc2--;
ArcNode* temp1;
ArcNode* p1 = (ArcNode*)malloc(sizeof(ArcNode));//建立一个新的边关系,并对其赋值
p1->loc = loc2;//使用头插法
temp1 = graph[loc1].firstarc;
graph[loc1].firstarc = p1;
p1->nextarc = temp1;
ArcNode* temp2;//因为所建立的图为无向图,所以要将两个节点之间的关系在建立一遍
ArcNode* p2 = (ArcNode*)malloc(sizeof(ArcNode));
p2->loc = loc1;
temp2 = graph[loc2].firstarc;
graph[loc2].firstarc = p2;
p2->nextarc = temp2;
}

插入完所有节点之后,就可以进行广度优先搜索了,同样,也需要一个visited[]数组来记录哪些节点已经被访问过,因为采用的是邻接表的储存方法,所以很容易能知道一个节点的所有相关节点,只需要从头节点根据指针一直想后搜索,直到指针的值是NULL为止。
在遍历的时候,需要用到循环队列在访问一个节点的关联节点时,将他的关联节点依此入队,这个节点访问完成后,下一次从队尾出队一个元素,在对这个元素进行搜索,重复上述的入队过程,直到所有节点都被访问到。
使用循环队列的原因是因为节省空间。需要对队列指针进行取余,防止越界。
void BFS(VNode graph[],int visited[],int v)//给出图,访问数组还有一个开始顶点
{
printf("访问节点%d\n",v);
visited[v] = 1;//已经访问过
queue[PHead++] = v;//v节点入队
while(!QueueEmpty())//队列非空
{
if(AllVisited(visited) == 1)//所有节点都被访问过
{
printf("所有节点都以访问\n");
return ;
}
int temp = queue[PTail];//将队尾元素出队,
queue[PTail] = 100;//队列元素初始化
PTail++;//尾指针前移
PTail = PTail % 8;//避免越界
ArcNode* arc_temp = graph[temp].firstarc;//节点的第一个指针
while(arc_temp != NULL)//遍历这个节点的所又关联节点
{
if(visited[arc_temp->loc] == 0)//这个节点的关联节点没有被访问过
{
visited[arc_temp->loc] = 1;//表示已经被访问
printf("访问节点%d\n",arc_temp->loc);
queue[PHead++] = arc_temp->loc;//将这个节点入队
PHead = PHead % 8;//保证不会越界
}
arc_temp = arc_temp->nextarc;//寻找下一个关联节点
}
}
}
如果要遍历的是一棵树的话,深度优先搜索可以很快地走到叶子节点,而广度优先搜索的路径从根节点开始向四周所有可以走的路径蔓延。
深度优先搜索代码
#include广度优先搜索代码
#include