PLDA源代码分析(2)-PLDA_Verification
说明:此处的LDA对应于Linear Discriminant Analysis,PLDA即对应于Probabilistic LDA. 该代码对应的文章为ICCV2007 paper Probabilistic Linear Discriminant Analysis for Inferences About Identity,源代码可以从 Prince Vision Lab处下载。虽然源码虽然不长结构比较清楚,但是运用到了一定的矩阵知识,所以对源码分析稍作分析。
1、PLDA 训练(Training)源码分析
2、PLDA识别(Recognition)源码分析
3、PLDA相关应用
基本问题
Face verification是给出两张脸,我们判断它是否属于同一个人(不管这个人是谁),如下图所示两个样本x1和xp,那么一共有两个模型,M0表示他们不是同一个人,M1表明他们来自同一个人(由相同identity variable h产生)。
该程序就是计算两个样本属于同一个人的概率和属于不同人概率之比,若这个概率越大,我们认为他们属于同一个人的概率也越大。
该文件有三个子程序:
- PLDA_Verification. 主程序,计算这个概率之比。
- preProcessPLDAModel和preProcessPLDAData是预处理程序,为了子程序getLogLikeMatchPLDA方便。
- getLogLikeMatchPLDA. 计算参数X(可能只有一个样本)中的样本属于同一个人的概率。
PLDA_Verification
主程序。前半部分是调用preProcessPLDAModel和preProcessPLDAData对数据预处理,减少后面计算概率的复杂度。其中HIGHEST_N表示最多有多少个样本来自同一人。HIGHEST_N = 2;
factorModel = preProcessPLDAModel(F, G, Sigma, HIGHEST_N);
Data1P = preProcessPLDAData(factorModel, Data1);
Data2P = preProcessPLDAData(factorModel, Data2);
那么如上图所示,M0模型时,样本属于不同的人,那么样本在M0模型下的概率为:
那么在M1模型的情况下,样本属于同一个人,它的概率为:
那么下面代码就是计算样本符合M1模型的概率和符合M0模型的概率之比(取对数,那么乘变为加,除变为减)
看几个加粗的变量:
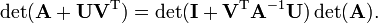


preProcessPLDAData
logLikeNoMatch = getLogLikeMatchPLDA(factorModel, Data1P)...
+ getLogLikeMatchPLDA(factorModel, Data2P);
logLikeMatch = getLogLikeMatchPLDA(factorModel, [Data1P, Data2P]);
LogLikeRatio = logLikeMatch - logLikeNoMatch;
getLogLikeMatchPLDA
先看这个计算概率的程序。我们知道,对概率值取对数我们可以得到:
这里x'是一个维数是nd的列向量。前面两项是一个常量,在程序中是factorModel.constTerm{N_DATA}.我们在子程序preProcessModel中计算。最后一项需要计算,这个矩阵大小会随着样本数量而成倍增加。直接计算有难度我们对它进行如下的变换:
我们设变量和如下所示:
那么根据矩阵逆定理(Binomial Inverse Theorem):
![]()
最终可以如下计算:
那么:
其中:
- 对应代码中的dataPP.quadTerm,在preProcessPLDAData子程序中计算。
- 对应代码中的sumWeightedData,它由dataPP(data).FTinvSx(在preProcessPLDAData子程序中计算)累加得到。
- 对应代码中的factorModel.invNFSPlusDiag{N_DATA},在preProcessPLDAModel子程序中得到。
最终计算概率的代码如下:
logLike = factorModel.constTerm{N_DATA};
sumWeightedData = zeros(N_HIDDEN, 1);
logTerm = 0;
for cData = 1 : N_DATA
logTerm = logTerm + dataPP(cData).quadTerm;
sumWeightedData = sumWeightedData + dataPP(cData).FTinvSx;
end
logLike = logLike - 0.5 *(logTerm - ...
(sumWeightedData' * factorModel.invNFSFPlusIDiag{N_DATA} * sumWeightedData));
returnpreProcessPLDAModel
该主程序主要是对PLDA模型进行预处理计算一些变量的值如下表格:
| 变量名 | 变量值 |
| invCovDiag | |
| GWeighted | |
| factorModel.invTerm | |
| factorModel.FTranspJ | |
| factorModel.AInv | |
| factorModel.U | |
| factorModel.V | |
| factorModel.MDLInvTerm | |
| factorModel.logDetJ | |
| factorModel.F | F |
| factorModel.G | G |
| factorModel.FWeighted | |
| factorModel.GWeighted | |
| factorModel.InvNFSFPlusDiag{n} | |
| logdetInvNFSDPlusDiag | |
| factorModel.constTerm{n} |
- factorModel.FTranspJ同样用的是矩阵逆定理(Binomial Inverse Theorem):
代码如下:
factorModel.FTranspJ = (F.*repmat(invCovDiag,1,N_HIDDEN_DIM))'-(F'*GWeighted)*factorModel.invTerm*GWeighted';- factorModel.logDetJ用到矩阵逆定理(Binomial Inverse Theorem)和矩阵行列式定理(Matrix determinant lemma).其中矩阵行列式定理如下:
那么该变量可如下计算:
其中最后一步利用公式: 。
具体代码如下所示:
[U L V]=svd(factorModel.MDLInvTerm);
factorModel.logDetJ =sum(log(diag(L))) + sum(log(invCovDiag));- factorModel.InvNFSFPlusDiag{n}参见SVD和PCA
- factorModel.constTerm{n}后半部分,可以如下计算:
分别对应于
logdetInvNFSDPlusDiag和
factorModel.logDetJ,代码部分如下所示:
for cN = 1 : HIGHEST_N
[U, L, V] = svd(cN*F'*factorModel.FWeighted+eye(N_HIDDEN_DIM));
DiagL = diag(L);
factorModel.invNFSFPlusIDiag{cN} = V * diag(1 ./ DiagL) * U';
logdetInvNFSFPlusIDiag = sum(log(1 ./ DiagL));
factorModel.constTerm{cN} = - (cN * N_DATA_DIM / 2) * log(2* pi)...
+ cN / 2 * factorModel.logDetJ + 0.5 * logdetInvNFSFPlusIDiag;
endpreProcessPLDAData
该子程序主要计算 ,对应程序中的quadTerm。根据
矩阵逆定理( Binomial Inverse Theorem
)可以如下计算:
分别对应程序中的quadTerm1和quadTerm2,代码如下:
for cData = 1 : N_DATA
quadTerm1 = (factorModel.AInv.*data(:,cData))'*data(:,cData);
quadTerm2 = (data(:,cData)'*factorModel.GWeighted)*factorModel.invTerm*(factorModel.GWeighted'*data(:,cData));
quadTerm = quadTerm1-quadTerm2;
dataPP(cData).quadTerm = quadTerm;
end