zkw线段树详解
转载自:http://blog.csdn.net/qq_18455665/article/details/50989113
前言
- 首先说说出处:
- 清华大学 张昆玮(zkw) - ppt 《统计的力量》
- 本文
(辣鸡)编辑:BeiYu - 写这篇博客的原因:
1.zkw线段树非递归,效率高,代码短
2.网上关于zkw线段树的讲解实在是太少了
3.个人感觉很实用
更新日志
- 20160327-Part 1(zkw线段树的建立)
- 20160329-Part 2(单点操作)
- 20160329-Part 3(区间操作)
Part 1
来说说它的构造
线段树的堆式储存
![]()
我们来转成二进制看看
![]()
小学生问题:找规律
规律是很显然的
- 一个节点的父节点是这个数左移1,这个位运算就是低位舍弃,所有数字左移一位
- 一个节点的子节点是这个数右移1,是左节点,右移1+1是右节点
- 同一层的节点是依次递增的,第n层有2^(n-1)个节点
- 最后一层有多少节点,值域就是多少(这个很重要)
有了这些规律就可以开始着手建树了
- 查询区间[1,n]
最后一层不是2的次幂怎么办?
开到2的次幂!后面的空间我不要了!就是这么任性!
Build函数就这么出来了!找到不小于n的2的次幂
直接输入叶节点的信息
int n,M,q;int d[N<<1];
inline void Build(int n){
for(M=1;M维护父节点信息?
倒叙访问,每个节点访问的时候它的子节点已经处理过辣!
- 维护区间和?
for(int i=M-1;i;--i) d[i]=d[i<<1]+d[i<<1|1];- 维护最大值?
for(int i=M-1;i;--i) d[i]=max(d[i<<1],d[i<<1|1]);- 维护最小值?
for(int i=M-1;i;--i) d[i]=min(d[i<<1],d[i<<1|1]); 如果你是压行选手的话(比如我),建树的代码只需要两行。
是不是特别Easy!
新技能Get√
Part 2
单点操作
- 单点修改
void Change(int x,int v){
d[M+x]+=v;
}只是这么简单?当然不是,跟线段树一样,我们要更新它的父节点!
void Change(int x,int v){
d[x=M+x]+=v;
while(x) d[x>>=1]=d[x<<1]+d[x<<1|1];
}没了?没了。
- 单点查询(差分思想,后面会用到)
把d维护的值修改一下,变成维护它与父节点的差值(为后面的RMQ问题做准备)
建树的过程就要修改一下咯!
void Build(int n){
for(M=1;M<=n+1;M<<=1);for(int i=M+1;i<=M+n;i++) d[i]=in();
for(int i=M-1;i;--i) d[i]=min(d[i<<1],d[i<<1|1]),d[i<<1]-=d[i],d[i<<1|1]-=d[i];
}在当前情况下的查询
void Sum(int x,int res=0){
while(x) res+=d[x],x>>=1;return res;
}Part 3
区间操作
询问区间和,把[s,t]闭区间换成(s,t)开区间来计算
int Sum(int s,int t,int Ans=0){
for (s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1){
if(~s&1) Ans+=d[s^1];
if( t&1) Ans+=d[t^1];
}return Ans;
}- 为什么
~s&1? -
为什么
t&1?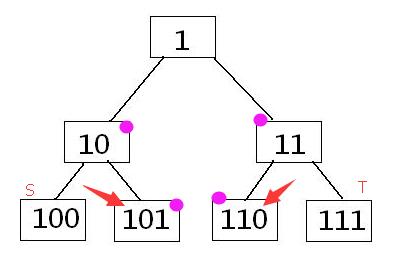
变成开区间了以后,如果s是左儿子,那么它的兄弟节点一定在区间内,同理,如果t是右儿子,那么它的兄弟节点也一定在区间内! -
这样计算不会重复吗?
答案是会的!所以注意迭代的出口s^t^1
如果s,t就是兄弟节点,那么也就迭代完成了。
代码简单,即使背过也不难QuQ
- 区间最小值
void Sum(int s,int t,int L=0,int R=0){
for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1){
L+=d[s],R+=d[t];
if(~s&1) L=min(L,d[s^1]);
if(t&1) R=min(R,d[t^1]);
}
int res=min(L,R);while(s) res+=d[s>>=1];
} 不要忘记最后的统计!
还有就是建树的时候是用的最大值还是最小值,这个一定要注意,影响到差分。
- 区间最大值
void Sum(int s,int t,int L=0,int R=0){
for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1){
L+=d[s],R+=d[t];
if(~s&1) L=max(L,d[s^1]);
if(t&1) R=max(R,d[t^1]);
}
int res=max(L,R);while(s) res+=d[s>>=1];
}同理。
- 区间加法
void Add(int s,int t,int v,int A=0){
for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1){
if(~s&1) d[s^1]+=v;if(t&1) d[t^1]+=v;
A=min(d[s],d[s^1]);d[s]-=A,d[s^1]-=A,d[s>>1]+=A;
A=min(d[t],d[t^1]);d[t]-=A,d[t^1]-=A,d[t>>1]+=A;
}
while(s) A=min(d[s],d[s^1]),d[s]-=A,d[s^1]-=A,d[s>>=1]+=A;
}zkw线段树小试牛刀(code来自hzwer.com)
#include
#include
#define M 261244
using namespace std;
int tr[524289];
void query(int s,int t)
{
int ans=0;
for(s=s+M-1,t=t+M+1;s^t^1;s>>=1,t>>=1)
{
if(~s&1)ans+=tr[s^1];
if(t&1)ans+=tr[t^1];
}
printf("%d\n",ans);
}
void change(int x,int y)
{
for(tr[x+=M]+=y,x>>=1;x;x>>=1)
tr[x]=tr[x<<1]+tr[x<<1|1];
}
int main()
{
int n,m,f,x,y;
scanf("%d",&n);
for(int i=1;i<=n;i++){scanf("%d",&x);change(i,x);}
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&f,&x,&y);
if(f==1)change(x,y);
else query(x,y);
}
return 0;
} poj3468(code来自网络)
#include
#include
#include
#define N ((131072 << 1) + 10) //表示节点个数->不小于区间长度+2的最小2的正整数次幂*2+10
typedef long long LL;
inline int getc() {
static const int L = 1 << 15;
static char buf[L] , *S = buf , *T = buf;
if (S == T) {
T = (S = buf) + fread(buf , 1 , L , stdin);
if (S == T)
return EOF;
}
return *S++;
}
inline int getint() {
static char c;
while(!isdigit(c = getc()) && c != '-');
bool sign = (c == '-');
int tmp = sign ? 0 : c - '0';
while(isdigit(c = getc()))
tmp = (tmp << 1) + (tmp << 3) + c - '0';
return sign ? -tmp : tmp;
}
inline char getch() {
char c;
while((c = getc()) != 'Q' && c != 'C');
return c;
}
int M; //底层的节点数
int dl[N] , dr[N]; //节点的左右端点
LL sum[N]; //节点的区间和
LL add[N]; //节点的区间加上一个数的标记
#define l(x) (x<<1) //x的左儿子,利用堆的性质
#define r(x) ((x<<1)|1) //x的右儿子,利用堆的性质
void pushdown(int x) { //下传标记
if (add[x]&&x>= 1)
stack[++top] = tmp;
while(top--)
pushdown(stack[top]);
}
LL query(int tl , int tr) { //求和
LL res=0;
int insl = 0, insr = 0; //两侧第一个有用节点
for(tl=tl+M-1,tr=tr+M+1;tl^tr^1;tl>>=1,tr>>=1) {
if (~tl&1) {
if (!insl)
upd(insl=tl^1);
res+=sum[tl^1];
}
if (tr&1) {
if(!insr)
upd(insr=tl^1)
res+=sum[tr^1];
}
}
return res;
}
void modify(int tl , int tr , int val) { //修改
int insl = 0, insr = 0;
for(tl=tl+M-1,tr=tr+M+1;tl^tr^1;tl>>=1,tr>>=1) {
if (~tl&1) {
if (!insl)
upd(insl=tl^1);
add[tl^1]+=val;
sum[tl^1]+=(LL)val*(dr[tl^1]-dl[tl^1]+1);
}
if (tr&1) {
if (!insr)
upd(insr=tr^1);
add[tr^1]+=val;
sum[tr^1]+=(LL)val*(dr[tr^1]-dl[tr^1]+1);
}
}
for(insl=insl>>1;insl;insl>>=1) //一路update
sum[insl]=sum[l(insl)]+sum[r(insl)];
for(insr=insr>>1;insr;insr>>=1)
sum[insr]=sum[l(insr)]+sum[r(insr)];
}
inline void swap(int &a , int &b) {
int tmp = a;
a = b;
b = tmp;
}
int main() {
//freopen("tt.in" , "r" , stdin);
int n , ask;
n = getint();
ask = getint();
int i;
for(M = 1 ; M < (n + 2) ; M <<= 1);
for(i = 1 ; i <= n ; ++i)
sum[M + i] = getint() , dl[M + i] = dr[M + i] = i; //建树
for(i = M - 1; i >= 1 ; --i) { //预处理节点左右端点
sum[i] = sum[l(i)] + sum[r(i)];
dl[i] = dl[l(i)];
dr[i] = dr[r(i)];
}
char s;
int a , b , x;
while(ask--) {
s = getch();
if (s == 'Q') {
a = getint();
b = getint();
if (a > b)
swap(a , b);
printf("%lld\n" , query(a , b));
}
else {
a = getint();
b = getint();
x = getint();
if (a > b)
swap(a , b);
modify(a , b , x);
}
}
return 0;
} #include
#include
#include
#include
#include
#include
#define mp(x,y) make_pair(x,y)
using namespace std;
const int N = 100000;
const int inf = 0x3f3f3f3f;
int a[N + 10];
int b[N + 10];
int M;
int lq, rq;
vector > s[N * 22];
void add(int id, int cur)
{
cur += M;
int lat = 0;
if (s[cur].size())
lat = s[cur][s[cur].size() - 1].second;
s[cur].push_back(mp(id, ++lat));
for (cur >>= 1; cur; cur >>= 1)
{
int l = 0;
if (s[cur << 1].size())
l = s[cur << 1][s[cur << 1].size() - 1].second;
int r = 0;
if (s[cur << 1 | 1].size())
r = s[cur << 1 | 1][s[cur << 1 | 1].size() - 1].second;
s[cur].push_back(mp(id, l + r));
}
}
int Q(int id, int k)
{
if (id >= M) return id - M;
int l = id << 1, r = l ^ 1;
int ll = lower_bound(s[l].begin(), s[l].end(), mp(lq, inf)) - s[l].begin() - 1;
int rr = lower_bound(s[l].begin(), s[l].end(), mp(rq, inf)) - s[l].begin() - 1;
int kk = 0;
if (rr >= 0)kk = s[l][rr].second;
if (ll >= 0)kk = s[l][rr].second - s[l][ll].second;
if (kk < k)return Q(r, k - kk);
return Q(l, k);
}
int main()
{
int n, m;
while (~scanf("%d%d", &n, &m))
{
for (int i = 0; i < n; i++)
{
scanf("%d", a + i);
b[i] = a[i];
}
sort(b, b + n);
int nn = unique(b, b + n) - b;
for (M = 1; M < nn; M <<= 1);
for (int i = 1; i < M + M; i++)
{
s[i].clear();
//s[i].push_back(mp(0, 0));
}
for (int i = 0; i < n; i++)
{
int id = lower_bound(b, b + nn, a[i]) - b;
add(i + 1, id);
}
while (m--)
{
int k;
scanf("%d %d %d", &lq, &rq, &k);
lq--;
int x = Q(1, k);
printf("%d\n", b[x]);
}
}
return 0;
} const int N = 1e5;
struct node
{
int sum, d, v;
int l, r;
void init()
{
d = 0;
v = -1;
}
void cb(node ls, node rs)
{
sum = ls.sum + rs.sum;
l = ls.l, r = rs.r;
}
int len()
{
return r - l + 1;
}
void V(int x)
{
sum = len() * x;
d = 0;
v = x;
}
void D(int x)
{
sum += len() * x;
d += x;
}
};
struct tree
{
int m, h;
node g[N << 2];
void init(int n)
{
for (m = h = 1; m < n + 2; m <<= 1, h++);
int i = 0;
for (; i <= m; i++)
{
g[i].init();
g[i].sum = 0;
}
for (; i <= m + n; i++)
{
g[i].init();
scanf("%d", &g[i].sum);
g[i].l = g[i].r = i - m;
}
for (; i < m + m; i++)
{
g[i].init();
g[i].sum = 0;
g[i].l = g[i].r = i - m;
}
for (i = m - 1; i > 0; i--)
g[i].cb(g[i << 1], g[i << 1 | 1]);
}
void dn(int x)
{
for (int i = h - 1; i > 0; i--)
{
int f = x >> i;
if (g[f].v != -1)
{
g[f << 1].V(g[f].v);
g[f << 1 | 1].V(g[f].v);
}
if (g[f].d)
{
g[f << 1].D(g[f].d);
g[f << 1 | 1].D(g[f].d);
}
g[f].v = -1;
g[f].d = 0;
}
}
void up(int x)
{
for (x >>= 1; x; x >>= 1)
{
if (g[x].v != -1)continue;
int d = g[x].d;
g[x].d = 0;
g[x].cb(g[x << 1], g[x << 1 | 1]);
g[x].D(d);
}
}
void update(int l, int r, int x, int o)
{
l += m - 1, r += m + 1;
dn(l), dn(r);
for (int s = l, t = r; s ^ t ^ 1; s >>= 1, t >>= 1)
{
if (~s & 1)
{
if (o)
g[s ^ 1].V(x);
else
g[s ^ 1].D(x);
}
if (t & 1)
{
if (o)
g[t ^ 1].V(x);
else
g[t ^ 1].D(x);
}
}
up(l), up(r);
}
int Q(int l, int r)
{
int ans = 0;
l += m - 1, r += m + 1;
dn(l), dn(r);
for (int s = l, t = r; s ^ t ^ 1; s >>= 1, t >>= 1)
{
if (~s & 1)ans += g[s ^ 1].sum;
if (t & 1)ans += g[t ^ 1].sum;
}
return ans;
}
}; #include
#include
#include
#include
#include
#include
using namespace std;
const int W = 1000;
int m;
struct tree
{
int d[W << 2];
void o()
{
for (int i = 1; i < m + m; i++)d[i] = 0;
}
void Xor(int l, int r)
{
l += m - 1, r += m + 1;
for (int s = l, t = r; s ^ t ^ 1; s >>= 1, t >>= 1)
{
if (~s & 1)d[s ^ 1] ^= 1;
if (t & 1)d[t ^ 1] ^= 1;
}
}
} g[W << 2];
void chu()
{
for (int i = 1; i < m + m; i++)
g[i].o();
}
void Xor(int lx, int ly, int rx, int ry)
{
lx += m - 1, rx += m + 1;
for (int s = lx, t = rx; s ^ t ^ 1; s >>= 1, t >>= 1)
{
if (~s & 1)g[s ^ 1].Xor(ly, ry);
if (t & 1)g[t ^ 1].Xor(ly, ry);
}
}
int Q(int x, int y)
{
int ans = 0;
for (int xx = x + m; xx; xx >>= 1)
{
for (int yy = y + m; yy; yy >>= 1)
{
ans ^= g[xx].d[yy];
}
}
return ans;
}
int main()
{
int T;
cin >> T;
int fl = 0;
while (T--)
{
if (fl)
{
printf("\n");
}
fl = 1;
int N, M;
cin >> N >> M;
for (m = 1; m < N + 2; m <<= 1);
chu();
while (M--)
{
char o[4];
scanf("%s", o);
if (*o == 'Q')
{
int x, y;
scanf("%d%d", &x, &y);
printf("%d\n", Q(x, y));
}
else
{
int lx, ly, rx, ry;
scanf("%d%d%d%d", &lx, &ly, &rx, &ry);
Xor(lx, ly, rx, ry);
}
}
}
return 0;
} #include
#include
#include
#include
#include
#include
using namespace std;
const int N = 111;
int n;
vector y;
struct node
{
double s;
int c;
int l, r;
void chu(double ss, int cc, int ll, int rr)
{
s = ss;
c = cc;
l = ll, r = rr;
}
double len()
{
return y[r] - y[l - 1];
}
} g[N << 4];
int M;
void init(int n)
{
for (M = 1; M < n + 2; M <<= 1);
g[M].chu(0, 0, 1, 1);
for (int i = 1; i <= n; i++)
g[i + M].chu(0, 0, i, i);
for (int i = n + 1; i < M; i++)
g[i + M].chu(0, 0, n, n);
for (int i = M - 1; i > 0; i--)
g[i].chu(0, 0, g[i << 1].l, g[i << 1 | 1].r);
}
struct line
{
double x, yl, yr;
int d;
line() {}
line(double x, double yl, double yr, int dd): x(x), yl(yl), yr(yr), d(dd) {}
bool operator < (const line &cc)const
{
return x < cc.x || (x == cc.x && d > cc.d);
}
};
vectorL;
void one(int x)
{
if (x >= M)
{
g[x].s = g[x].c ? g[x].len() : 0;
return;
}
g[x].s = g[x].c ? g[x].len() : g[x << 1].s + g[x << 1 | 1].s;
}
void up(int x)
{
for (; x; x >>= 1)
one(x);
}
void add(int l, int r, int d)
{
if (l > r)return;
l += M - 1, r += M + 1;
for (int s = l, t = r; s ^ t ^ 1; s >>= 1, t >>= 1)
{
if (~s & 1)
{
g[s ^ 1].c += d;
one(s ^ 1);
}
if (t & 1)
{
g[t ^ 1].c += d;
one(t ^ 1);
}
}
up(l);
up(r);
}
double sol()
{
y.clear();
L.clear();
for (int i = 0; i < n; i++)
{
double lx, ly, rx, ry;
scanf("%lf %lf %lf %lf", &lx, &ly, &rx, &ry);
L.push_back(line(lx, ly, ry, 1));
L.push_back(line(rx, ly, ry, -1));
y.push_back(ly);
y.push_back(ry);
}
sort(y.begin(), y.end());
y.erase(unique(y.begin(), y.end()), y.end());
init(y.size());
sort(L.begin(), L.end());
n = L.size() - 1;
double ans = 0;
for (int i = 0; i < n; i++)
{
int l = upper_bound(y.begin(), y.end(), L[i].yl + 1e-8) - y.begin();
int r = upper_bound(y.begin(), y.end(), L[i].yr + 1e-8) - y.begin() - 1;
add(l, r, L[i].d);
ans += g[1].s * (L[i + 1].x - L[i].x);
}
return ans;
}
int main()
{
int ca = 1;
while (cin >> n && n)
{
printf("Test case #%d\nTotal explored area: %.2f\n\n", ca++, sol());
}
return 0;
}