LeetCode之动态规划专题

5.最长回文子串

• 暴力法，用双重for循环列举所有子串（On2），判断每个子串是否是回文（On）
• 中心扩展法，以每个字母为中心，向外扩展。
• 动态规划。dp[i][j]表示从i到j这个子串是不是回文（bool）。

dp[i][j] = s[i]==s[j] && dp[i+1][j-1]

class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp=[]
        for _ in range(len(s)):
            dp.append([0]*len(s))
        res=''
        for i in range(len(s)-1,-1,-1):
            for j in range(i, len(s)):
                dp[i][j]=(s[j]==s[i])and(j-i<2 or dp[i+1][j-1]) # j-i<2代表相邻或重叠
                if dp[i][j] and j-i+1>len(res):
                    res=s[i:j+1]
        return res

62. 不同路径

同剑指offer中最大礼物价值。二维数组dp[i][j]记录从左上角到达（i，j）有多少路径。

• 动态规划，从左至右，从上到下依次加。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[]
        for _ in range(m):
            dp.append([0]*n)
        dp[0][0]=1
        for i in range(m):
            for j in range(n):
                if i==0 or j==0:
                    dp[i][j]=1
                    continue
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[m-1][n-1]

还可以用一位数组优化。

63. 不同路径II

在62题的基础上，增加了障碍物，遇到障碍物，则dp[i][j]为0。预先处理第一行和第一列的数据。

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m,n=len(obstacleGrid), len(obstacleGrid[0])
        dp=[]
        for _ in range(m):
            dp.append([0]*n)
        for i in range(m):
            for j in range(n):
                if i==0:
                    if j==0:
                        if obstacleGrid[i][j]:
                            return 0
                        dp[0][0]=1
                        continue
                    else:
                        if obstacleGrid[i][j]:
                            dp[i][j]=0
                        else:
                            dp[i][j]=dp[i][j-1]
                        continue
                if j==0:
                    if obstacleGrid[i][j]:
                        dp[i][j]=0
                    else: 
                        dp[i][j]=dp[i-1][j]
                    continue
                if obstacleGrid[i][j]:
                    dp[i][j]=0
                else:
                    dp[i][j]=dp[i][j-1]+dp[i-1][j]
        return dp[m-1][n-1]      

64.最小路径

同最大礼物问题

72. 编辑距离

对“dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。”的补充理解：
以 word1 为 “horse”，word2 为 “ros”，且 dp[5][3] 为例，即要将 word1的前 5 个字符转换为 word2的前 3 个字符，也就是将 horse 转换为 ros，因此有：
(1) dp[i-1][j-1]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 2 个字符 ro，然后将第五个字符 word1[4]（因为下标基数以 0 开始） 由 e 替换为 s（即替换为 word2 的第三个字符，word2[2]）
(2) dp[i][j-1]，即先将 word1 的前 5 个字符 horse 转换为 word2 的前 2 个字符 ro，然后在末尾补充一个 s，即插入操作
(3) dp[i-1][j]，即先将 word1 的前 4 个字符 hors 转换为 word2 的前 3 个字符 ros，然后删除 word1 的第 5 个字符

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m,n=len(word1),len(word2)
        if m*n == 0:
            return m+n
        dp=[[0]*(n+1) for _ in range(m+1)]
        for i in range(m+1):
            dp[i][0]=i
        for j in range(n+1):
            dp[0][j]=j
        for i in range(m):
            for j in range(n):
                if word1[i]== word2[j]:
                    dp[i+1][j+1]=dp[i][j]
                else:
                    dp[i+1][j+1]=min(
                       1+dp[i+1][j], # 添加
                       1+dp[i][j+1], # 删除
                       1+dp[i][j] # 替换
                    )
        return dp[-1][-1]  

264. 丑数

• 三指针法，前面丑数的2,3，5倍中，且超过最后一个丑数，选择最小的作为新丑数。

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        if n <=0:
            return None
        index = 1
        n2 = n3 = n5 = 0
        res = [1]
        while index < n:
            start = min(2*res[n2], 3*res[n3], 5*res[n5])
            res.append(start)
            while 2 * res[n2] <= start:
                n2 += 1
            while 3 * res[n3] <= start:
                n3 += 1
            while 5 * res[n5] <= start:
                n5 += 1
            index += 1
        return res[-1]

279. 完全平方数

dp[i]为将i拆分为完全平方数字所需要的最小数目。

class Solution:
    def numSquares(self, n: int) -> int:
        if n <=0:
            return 0
        dp = [0]*(n+1)
        for i in range(1, n+1):
            j = 1
            dp[i]=i
            while (i - j**2) >= 0:
                dp[i] = min(dp[i], dp[i-j**2]+1)
                j += 1
        return dp[-1]

300. 最长上升子序列

dp[i] 为从0-i范围内，以i为终点的最大上升子序列。因为最大上升子序列的终点未必是在n-1的位置上，所以返回的是max(dp)。

dp[i] = max(dp[i-k]+1) if nums[i] > nums[i-k] else 1, k in {1, i-1}

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        dp = [1] * (len(nums)+1)
        dp[0] = 0
        for i in range(1, len(nums)+1):
            temp = 1
            for j in range(1, i):
                if nums[i-1] > nums[i-1-j]:
                    temp=max(temp, dp[i-j]+1)
            dp[i] = temp
        return max(dp)

304. 二维区域和检索

• dp[i][j] = 前面和上面的值相加，加上当期位置的数字，再减去重复的部分dp[i-1][j-1]

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.matrix = matrix
        self.m = len(matrix)
        self.flag=True
        if not matrix:
            self.flag=False
            return
        self.n = len(matrix[0])
        self.dp = [[0]*(self.n+1) for _ in range(self.m+1)]
        for i in range(1,self.m+1):
            for j in range(1, self.n+1):
                self.dp[i][j] = self.matrix[i-1][j-1]+self.dp[i-1][j] + self.dp[i][j-1] - self.dp[i-1][j-1]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        if not self.flag:
            return 0
        return self.dp[row2+1][col2+1] - self.dp[row1][col2+1] - self.dp[row2+1][col1] + self.dp[row1][col1]

96. 不同的二叉搜索树

• G(n): 是长度为n的序列的不同二叉搜索树个数；
• F(i,n)：以i为根的二叉搜索树个数。总共有n个节点
• $G(n)={\sum }_{i}F(i,n),i\in 1,...,n$
• 而F(i,n)怎么定义？ 当以i为根，i左边的全部是左子树部分，i右边的全部是右子树部分。F(i,n) = G(i-1)*G(n-i). （左子树的个数 * 右子树的个数）

class Solution:
    def numTrees(self, n: int) -> int:      
        G = [0]*(n+1)
        G[0], G[1] = 1, 1
        for i in range(2, n+1):
            for j in range(1, i+1):
                G[i] += G[j-1] * G[i-j]
        return G[n]

95 不用的二叉搜索树II

这题是基于第96题。96题只需要求出有多少不同组合的二叉树数目。但这道题需要我们生成这些二叉树，就是需要记录下来。
其实这道题，我感觉不算是动态规划的题目了，因为代码的形式更加向全排列或者说回溯法。

• 1到n都能是根节点，所以放到for循环中，当i为根节点，i左边是左子树，i右边是右子树。
• 对于左子树的根节点，可以在1至i-1中选择，这又是一个for循环，右子树同理。因此，for循环内部是for循环，整个代码形式是for之中用递归。分别对左边和右边递归，得到做子树的根和右子树的根。可以看成是由底至顶，先搭建最底下的。

class Solution:
    def generateTrees(self, n: int) -> List[TreeNode]:
        def core(start, end):
            res = []
            if start > end:
                return [None,]
            for i in range(start, end +1):
                left = core(start, i-1)
                right = core(i+1, end)
                for l in left:
                    for r in right:
                        node=TreeNode(i)
                        node.left=l
                        node.right=r
                        res.append(node)
            return res
        return core(1, n) if n else []

91. 解码方法

典型的动态规划问题，A-Z对应了1-26，输入数字字符串，求出解码方法的最大数目。递归方程是 f[n] = f[n-1] + g* f[n-2]， 如果s[n-1:n+1]在10-26之间，g为1.

class Solution:
    def numDecodings(self, s: str) -> int:
        size = len(s)
        #特判
        if size == 0:
            return 0
        dp = [0]*(size+1)
        dp[0] = 1 
        for i in range(1,size+1):
            t = int(s[i-1])
            if t>=1 and t<=9:
                dp[i] += dp[i-1] #最后一个数字解密成一个字母
            if i >=2:#下面这种情况至少要有两个字符
                t = int(s[i-2])*10 + int(s[i-1])
                if t>=10 and t<=26:
                    dp[i] += dp[i-2]#最后两个数字解密成一个一个字母
        return dp[-1]

120. 三角形最小路径和

下面的代码没有采用空间优化。dp是和输入大小一样的空间。实际上，dp可以只用一个一维的大小为n的数组。

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        dp=[]
        height=len(triangle)
        for h in range(height):
            dp.append([0]*(h+1))
        dp[0][0]=triangle[0][0]
        for i in range(1,height):
            for j in range(i+1):
                if j==0: # 处理最左边，只有一个选择
                    dp[i][j]=dp[i-1][0]+triangle[i][j]
                    continue
                if j== i: # 处理最右边， 也只有一个选择
                    dp[i][j]=dp[i-1][-1]+triangle[i][j]
                    continue
                dp[i][j]=min(dp[i-1][j-1]+triangle[i][j],
                dp[i-1][j]+triangle[i][j])
            
        return min(dp[-1])
                

139. 单词拆分

我采用的是回溯法，即暴力法，并且用mask剪枝。
思路是：dic记录下有什么单词需要匹配。start指针指向单词开头位置，end指向单词尾部位置。滑动end直到匹配到某个字符，如果匹配不到，start这个位置会被mask记录为失败匹配，实现剪枝。

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        dic={}
        mask=[1]*(len(s)+1)
        for l in wordDict:
            dic[l]=0
        return self.unfold(s,dic,0,mask)


    def unfold(self,s,c,start,mask):
        if mask[start] == 0:
            return False
        if start==len(s):
            return True
        for end in range(start, len(s)):
            word=s[start:end+1]
            if word in c:
                c[word]+=1
                if self.unfold(s,c,end+1,mask):
                    return True
                c[word]-=1
        mask[start]=0
        return False

152. 乘法最大子数组

求一个数组内，最大的连续子数组的乘积
因为涉及到负数，其实这道题还是不好处理。所以需要两个数组作为dp，一个记录为i为结尾的连续数组乘积的最小值，另一个记录以i为结尾的乘积最大值。

其实这两个数组可以合并为dp[i][k],k为0和1。dp[i][1]的含义是：为i为结尾的连续数组的乘积的最小值。
还可以优化空间，只用两个变量就行了。

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        if len(nums)<=1:
            return nums[0]
        res=nums[0]
        minv=[0]*len(nums)
        minv[0]=res # 初始化
        maxv=[0]*len(nums)
        maxv[0]=res # 初始化第1个位置
        for i in range(1,len(nums)):
            temp1=nums[i]*maxv[i-1]
            temp2=nums[i]*minv[i-1]
            minv[i]=min(temp2,temp1,nums[i])
            maxv[i]=max(temp1,temp2,nums[i])
            res=max(res,maxv[i])
        return res

377.组合总数IV

这道题和零钱兑换有点像，只不过零钱兑换要求的是，能兑换出target的最少硬币数目。这道题则要求能兑换出零钱的最大组合数目。
核心就是更改递归方程：
$$f(n)=\sum _{j}f(n-Num[j])$$

class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [0] * (target+1)
        nums.sort()
        dp[0] = 1 # 当i == nums[j]时， 有一个直接用现有硬币兑换的组合
        for i in range(1, target+1 ):
            temp = 0
            for j in range(len(nums)):
                if i - nums[j] < 0:  # 边界条件
                    continue
                temp += dp[i - nums[j]]
            dp[i] = temp
        return dp[-1]
                

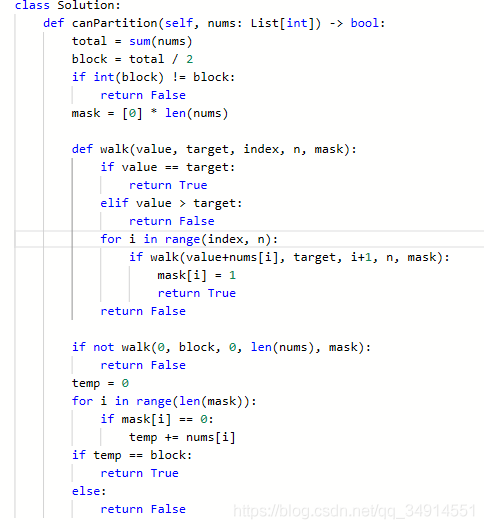
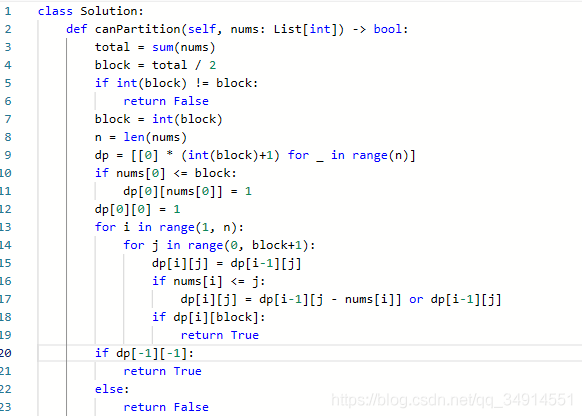
416.分割等和子集

先贴一段暴力回溯法，当然超时了

动态规划的思路是：dp[i][j]代表前i个数字中有没有和为j的组合。
递归方程为：dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i]]
当不选择nums[i]时，为dp[i-1][j] 当选择nums[i]，说明从第0到第i-1的数字中有和为j-nums[i]