c++写算法题:综合
c++算法题:综合
- 拯救公主
- 1251:仙岛求药
- dijkstra模板题
- 最短路
- 最小生成树模板
- kruskal法
- dfs综合体题
- codevs 1004 四子连棋
- dp动态规划
- codevs 1010 过河卒
- codevs 1014 装箱问题
- Floyd多源最短路
- codevs 1020 孪生蜘蛛
- 最小生成树
- prim算法
- codevs 1003 电话连线
- 最小生成树二刷
- 注意,数组一定要初始化,因为
- 动态规划
- 典型求大数余类型
- 935. Knight Dialer
拯救公主
百炼OJ, 题目链接

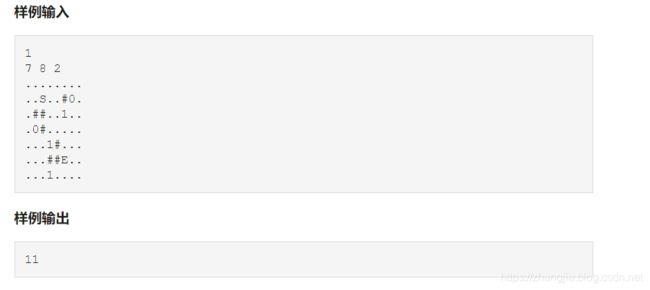
思路,典型的bfs问题,但需要处理的条件较多,此种题适合使用结构体来做,注意熟练使用结构体编程。
先贴上代码,以后再多写几遍,这里用到了状态压缩的方法记录宝石的数量。
#include #include > a(R,vector(C));
char a[200][200];
int dx[]={-1,1,0,0}; //上下左右
int dy[]={0,0,-1,1};
Node jewelNode[11];
int visited[200][200][1 << 5 - 1]; //宝石数目最大11111
int bit1Count(int value) {
unsigned int count = 0;
while (value > 0) { // until all bits are zero
if ((value & 1) == 1) // check lower bit
count++;
value >>= 1; // shift bits, removing lower bit
}
return count;
}
int bfs(Node *startNode,Node *endNode){
// 把startNode加入队列
visited[startNode->x][startNode->y][0] = 1; //置起点已经访问
queue<Node> q; // queue q行不行?
q.push(*startNode); //起点入队 q.push(startNode)?
while(!q.empty()){
Node node=q.front();q.pop(); // 取队首元素,出队
// 对四个方向遍历
for(int i=0;i<4;i++){
int newx=node.x+dx[i];
int newy=node.y+dy[i];
// 越界或者已经访问则跳过--------------visited数组为什么是三维的: 包含了宝石的情况
if(newx<0||newx>=R||newy<0||newy>=C||visited[newx][newy][node.num]==1) continue;
// 碰到#则走不通
if(a[newx][newy]=='#') continue;
// 其余情况均可走,标记为已经访问
visited[newx][newy][node.num]=1;
Node tempNode(newx, newy, node.num, node.depth+1); // 存下当前结果
// 碰到宝石
if(a[newx][newy]>='0'&&a[newx][newy]<='4'){
tempNode.num |= 1 << (a[newx][newy]-'0');
}
// 终止条件
if(newx==endNode->x&&newy==endNode->y&&bit1Count(tempNode.num)>=K) return tempNode.depth;
q.push(tempNode);
if(a[newx][newy]=='&'){ // 把所有传送门加入队列
for(int j=0;j<ct;j++){
if(jewelNode[j].x==newx&&jewelNode[j].y==newy) continue;
Node tNode(jewelNode[j].x, jewelNode[j].y, tempNode.num, tempNode.depth);
q.push(tNode);
}
}
// 如果遇到传送门
}
}
return -1;
}
int main()
{
int T=0;
cin>>T;
while(T--){
cin>>R>>C>>K; // R*C矩阵,K种类型宝石
// 读取字符矩阵
Node *startNode=NULL,*endNode=NULL;
for(int i=0;i<R;i++){
for(int j=0;j<C;j++){
cin>>a[i][j];
switch(a[i][j]){
case 'S': startNode=new Node(i,j,0,0);break; // 记录起点
case 'E': endNode=new Node(i,j,0,0);break; // 记录终点
case '$': jewelNode[ct++]=Node(i,j,0,0); // 记录宝石数量和位置
// 数组为什么就不可以 new Node(i,j,0,0)
}
}
}
int ans=bfs(startNode,endNode);
cout<<ans;
// ans == -1 ? (cout << "oop!" << endl) : (cout << ans << endl);
}
}
1251:仙岛求药
#includex<<" "<y<
}
}
}
}
return -1;
}
int main(){
// 读取字符矩阵
while(scanf("%d%d",&m,&n)!=EOF&&(m||n)) {
Node* startNode=NULL;
Node* endNode=NULL;
string s="";
// 初始化地图并记录地图起点和终点
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
cin>>map[i][j];
if(map[i][j]=='@') startNode=new Node(i,j,0);
else if(map[i][j]=='*') endNode=new Node(i,j,0);
}
}
int ans=bfs(startNode, endNode);
cout << ans << endl;
}
}
dijkstra模板题
最短路
题目链接
算法思路
-
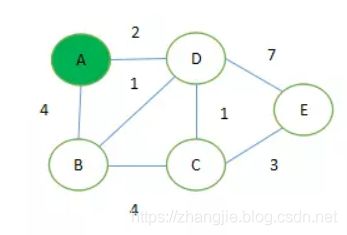
指定一个节点,例如我们要计算 ‘A’ 到其他节点的最短路径
-
引入两个集合(S、U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点(以及A到该点的路径,注意 如上图所示,A->C由于没有直接相连 初始时为∞)
-
初始化两个集合,S集合初始时 只有当前要计算的节点,A->A = 0,
U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞ -
从U集合中找出路径最短的点,加入S集合,例如 A->D = 2
-
更新U集合路径,if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 则更新U
-
循环执行 4、5 两步骤,直至遍历结束,得到A 到其他节点的最短路径
链接:https://www.jianshu.com/p/ff6db00ad866
算法模板:
- 求邻接矩阵
- 求dist矩阵
- 更新邻接矩阵
输入用例:
5 7
1 2 4
1 4 2
2 4 1
2 3 4
3 4 1
3 5 3
4 5 7
输出用例:
6
#include本题代码如下:
#include最小生成树模板
kruskal法
例题:
测试输入的第1行给出评估的道路条数N,村庄数目M;随后的 N 行,每行给出三个正整数,分别是两个村庄的编号,以及此两村庄间道路的成本(也是正整数)。为简单起见,村庄从1到M编号。
输入示例:
9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8
输出示例:
37
kruskal算法:
加边法,以下图A为起点,手动模拟结果如下所示:

Kruskal算法的高效实现需要一种称作并查集的结构。
Kruskal算法的过程:
- 将全部边按照权值由小到大排序。(使用结构体做邻接矩阵,需要写sort的cmp)
- 按顺序(边权由小到大的顺序)考虑每条边,只要这条边和我们已经选择的边不构成圈,就保留这条边,否则放弃这条边。(并查集检查find(S)和find(E)是否共一个掌门,若不共则非连通,加入生成树中,且合并S、V)
- 成功选择(n-1)条边后,形成一棵最小生成树,当然如果算法无法选择出(n-1)条边,则说明原图不连通。
代码模板:
#include dfs综合体题
codevs 1004 四子连棋
此题的难点在于
- 模拟棋的行走------------------------------使用空格位置做每次的起点
- 模拟黑白轮流执棋-----------------------需要记录上一次执棋的颜色
- 有黑白先后手之分------------------------分类深搜取最短的。
#include dp动态规划
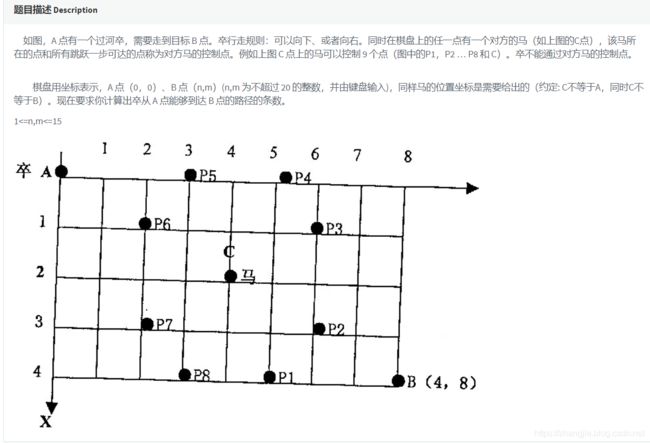
codevs 1010 过河卒
思路:典型的dp,先置马的控制点为1,令其他点均为0,0代表当前路可走,此处在处理的时候不需要判断边界条件,主要此处的巧妙使用。
//刷表法
#includecodevs 1014 装箱问题
#include Floyd多源最短路
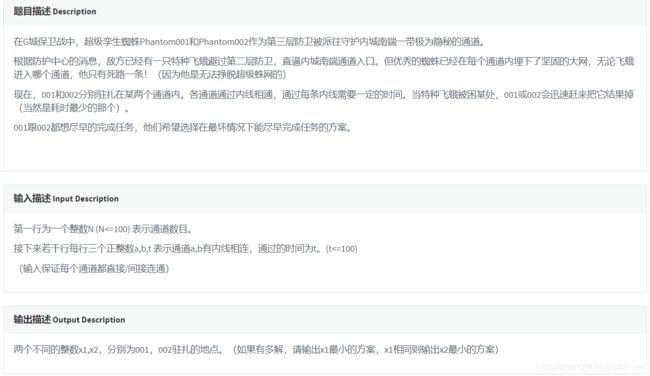
codevs 1020 孪生蜘蛛
#include 最小生成树
prim算法
codevs 1003 电话连线
给出邻接矩阵,要求求最小生成树的值。链接

注意这里的dist矩阵并不是某起点到其余点的距离,而是集合U到集合V的点的较小距离。
因而不像kruskal算法那样更新距离:
if (!visit[j]&&dis[j]>dis[pos]+map[pos][j]) {
dis[j]=dis[pos]+map[pos][j]; // 更新dis
}
#include最小生成树二刷
题目链接
**
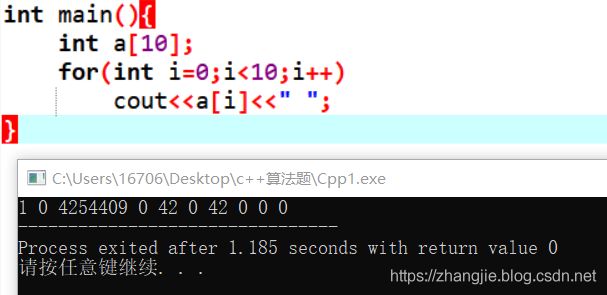
注意,数组一定要初始化,因为
最小生成树prim算法步骤
1.初始化邻接矩阵,对角线全0,连接不到则为inf
2.把起点加入集合U
3.for i 1 -> n : // 遍历剩下n-1个点
for j 0 -> n : // 遍历集合V,寻找最近的点
寻找集合V中点dist[]最小的值,记为min,并标记该点index
把最小点加入集合U中,累加该距离
for k 0 -> n : // 遍历集合U,更新集合U到集合V的距离
dist[k]=min(dist[k],map[index][k] ); // dist[i]代表未访问路径中,集合U和集合V中距离最小的两点距离
#include动态规划
典型求大数余类型
935. Knight Dialer

注意对于大数余法,我们有定律:(a+b)%c=((a%c)+(b%c))%c,因而我们常用以下形式来计算:
int add(int a, int b) { return (a + b) % MOD;}
因而以下代码结果是一样的
#include
using namespace std;
int MOD;
int add(int a, int b) { return (a + b) % MOD;}
int main(){
int a,b;
while(cin>>a>>b>>MOD)
cout< 代码如下:
class Solution {
const int MOD = 1e9+7;
int add(int a, int b) { return (a + b) % MOD; }
public:
int knightDialer(int N) {
int dp[5111][10]; // dp[i][j]表示走i步,当前处于第j位的走法有多少种
for(int i=0;i<10;i++)
dp[0][i] = 1;
for(int t=1;t<N;t++) {
dp[t][0] = add(dp[t-1][4], dp[t-1][6]);
dp[t][1] = add(dp[t-1][6], dp[t-1][8]);
dp[t][2] = add(dp[t-1][7], dp[t-1][9]);
dp[t][3] = add(dp[t-1][4], dp[t-1][8]);
dp[t][4] = add(dp[t-1][0], add(dp[t-1][9], dp[t-1][3]));
dp[t][5] = 0;
dp[t][6] = add(dp[t-1][1], add(dp[t-1][7], dp[t-1][0]));
dp[t][7] = add(dp[t-1][2], dp[t-1][6]);
dp[t][8] = add(dp[t-1][1], dp[t-1][3]);
dp[t][9] = add(dp[t-1][2], dp[t-1][4]);
}
int ans = 0;
for(int i=0;i<10;i++)
ans = add(ans, dp[N-1][i]);
return ans;
}
};