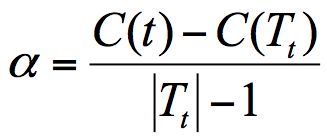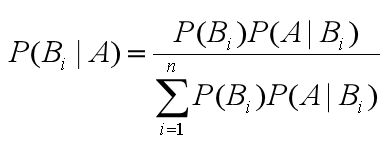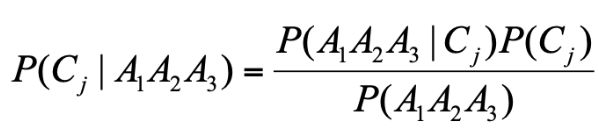数据分析3 - 算法篇

数据分析实战3.算法篇

• 分类算法：NB、C4.5、CART、SVM、KNN、Adaboost
• 聚类算法：K-Means、EM
• 关联分析：Apriori
• 链接分析：PageRank

---

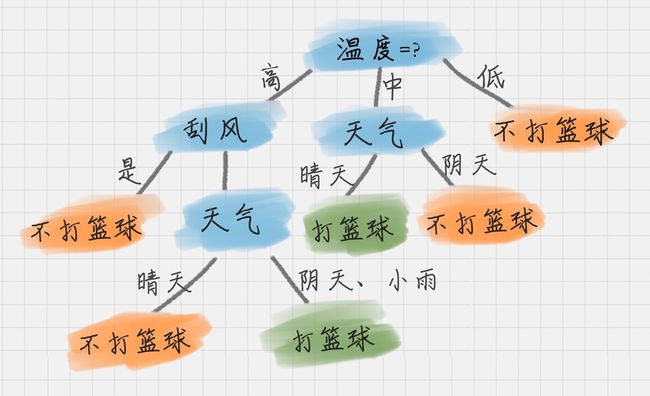
17 丨决策树（上）：要不要去打篮球？决策树来告诉你

决策树学习通常包括三个步骤

• 特征选择。选取最优特征来划分特征空间，用信息增益或者信息增益比来选择
• 决策树的生成。ID3、C4.5、CART
• 剪枝

纯度

你可以把决策树的构造过程理解成为寻找纯净划分的过程。数学上，我们可以用纯度来表示，纯度换一种方式来解释就是让目标变量的分歧最小。

信息熵（entropy）

它表示了信息的不确定度

p(i|t) 代表了节点 t 为分类 i 的概率，其中 log2 为取以 2 为底的对数。这里我们不是来介绍公式的，而是说存在一种度量，它能帮我们反映出来这个信息的不确定度。当不确定性越大时，它所包含的信息量也就越大，信息熵也就越高。

信息熵越大，纯度越低。当集合中的所有样本均匀混合时，信息熵最大，纯度最低。

我们在构造决策树的时候，会基于纯度来构建。而经典的 “不纯度”的指标有三种，分别是信息增益（ID3 算法）、信息增益率（C4.5 算法）以及基尼指数（Cart 算法）。

信息增益

信息增益指的就是划分可以带来纯度的提高，信息熵的下降。它的计算公式，是父亲节点的信息熵减去所有子节点的信息熵。在计算的过程中，我们会计算每个子节点的归一化信息熵，即按照每个子节点在父节点中出现的概率，来计算这些子节点的信息熵。所以信息增益的公式可以表示为：

公式中 D 是父亲节点，Di 是子节点，Gain(D,a) 中的 a 作为 D 节点的属性选择。

父节点

ID3 就是要将信息增益最大的节点作为父节点，这样可以得到纯度高的决策树。

如何判断要不要去打篮球？

所以 ID3 有一个缺陷就是，有些属性可能对分类任务没有太大作用，但是他们仍然可能会被选为最优属性。这种缺陷不是每次都会发生，只是存在一定的概率。在大部分情况下，ID3 都能生成不错的决策树分类。针对可能发生的缺陷，后人提出了新的算法进行改进。

在 ID3 算法上进行改进的 C4.5 算法

• 采用信息增益率

因为 ID3 在计算的时候，倾向于选择取值多的属性。为了避免这个问题，C4.5 采用信息增益率的方式来选择属性。信息增益率 = 信息增益 / 属性熵，具体的计算公式这里省略。

当属性有很多值的时候，相当于被划分成了许多份，虽然信息增益变大了，但是对于 C4.5 来说，属性熵也会变大，所以整体的信息增益率并不大。

• 采用悲观剪枝

ID3 构造决策树的时候，容易产生过拟合的情况。在 C4.5 中，会在决策树构造之后采用悲观剪枝（PEP），这样可以提升决策树的泛化能力。

悲观剪枝是后剪枝技术中的一种，通过递归估算每个内部节点的分类错误率，比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。

• 离散化处理连续属性

C4.5 可以处理连续属性的情况，对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性，不按照“高、中”划分，而是按照湿度值进行计算，那么湿度取什么值都有可能。该怎么选择这个阈值呢，C4.5 选择具有最高信息增益的划分所对应的阈值。

• 处理缺失值

针对数据集不完整的情况，C4.5 也可以进行处理。

ID3 & C4.5

现在我们总结下 ID3 和 C4.5 算法。首先 ID3 算法的优点是方法简单，缺点是对噪声敏感。训练数据如果有少量错误，可能会产生决策树分类错误。C4.5 在 ID3 的基础上，用信息增益率代替了信息增益，解决了噪声敏感的问题，并且可以对构造树进行剪枝、处理连续数值以及数值缺失等情况，但是由于 C4.5 需要对数据集进行多次扫描，算法效率相对较低。

总结

思考

请你用下面的例子来模拟下决策树的流程，假设好苹果的数据如下，请用 ID3 算法来给出好苹果的决策树。

---

18丨决策树（中）：CART，一棵是回归树，另一棵是分类树

CART 分类树的工作流程

我们知道决策树的核心就是寻找纯净的划分，因此引入了纯度的概念。在属性选择上，我们是通过统计“不纯度”来做判断的，ID3 是基于信息增益做判断，C4.5 在 ID3 的基础上做了改进，提出了信息增益率的概念。实际上 CART 分类树与 C4.5 算法类似，只是属性选择的指标采用的是基尼系数。

基尼系数本身反应了样本的不确定度。当基尼系数越小的时候，说明样本之间的差异性小，不确定程度低。分类的过程本身是一个不确定度降低的过程，即纯度的提升过程。所以 CART 算法在构造分类树的时候，会选择基尼系数最小的属性作为属性的划分。

假设 t 为节点，那么该节点的 GINI 系数的计算公式为：

这里 p(Ck|t) 表示节点 t 属于类别 Ck 的概率，节点 t 的基尼系数为 1 减去各类别 Ck 概率平方和。

节点 D 的基尼系数等于子节点 D1 和 D2 的归一化基尼系数之和，用公式表示为：

归一化基尼系数代表的是每个子节点的基尼系数乘以该节点占整体父亲节点 D 中的比例。

节点 D 被属性 A 划分后的基尼系数越大，样本集合的不确定性越大，也就是不纯度越高。

如何使用 CART 算法来创建分类树

通过上面的讲解你可以知道，CART 分类树实际上是基于基尼系数来做属性划分的。在 Python 的 sklearn 中，如果我们想要创建 CART 分类树，可以直接使用 DecisionTreeClassifier 这个类。创建这个类的时候，默认情况下 criterion 这个参数等于 gini，也就是按照基尼系数来选择属性划分，即默认采用的是 CART 分类树。

CART 回归树的工作流程

CART 回归树划分数据集的过程和分类树的过程是一样的，只是回归树得到的预测结果是连续值，而且评判“不纯度”的指标不同。在 CART 分类树中采用的是基尼系数作为标准，那么在 CART 回归树中，如何评价“不纯度”呢？实际上我们要根据样本的混乱程度，也就是样本的离散程度来评价“不纯度”。

样本的离散程度具体的计算方式是，先计算所有样本的均值，然后计算每个样本值到均值的差值。我们假设 x 为样本的个体，均值为 u。为了统计样本的离散程度，我们可以取差值的绝对值，或者方差。

其中差值的绝对值为样本值减去样本均值的绝对值：

方差为每个样本值减去样本均值的平方和除以样本个数：

所以这两种节点划分的标准，分别对应着两种目标函数最优化的标准，即用最小绝对偏差（LAD），或者使用最小二乘偏差（LSD）。这两种方式都可以让我们找到节点划分的方法，通常使用最小二乘偏差的情况更常见一些。

如何使用 CART 回归树做预测

这里我们使用到 sklearn 自带的波士顿房价数据集，该数据集给出了影响房价的一些指标，比如犯罪率，房产税等，最后给出了房价。

CART 决策树的剪枝

CART 决策树的剪枝主要采用的是 CCP 方法，它是一种后剪枝的方法，英文全称叫做 cost-complexity prune，中文叫做代价复杂度。这种剪枝方式用到一个指标叫做节点的表面误差率增益值，以此作为剪枝前后误差的定义。用公式表示则是：

其中 Tt 代表以 t 为根节点的子树，C(Tt) 表示节点 t 的子树没被裁剪时子树 Tt 的误差，C(t) 表示节点 t 的子树被剪枝后节点 t 的误差，|Tt|代子树 Tt 的叶子数，剪枝后，T 的叶子数减少了|Tt|-1。

所以节点的表面误差率增益值等于节点 t 的子树被剪枝后的误差变化除以剪掉的叶子数量。

• 生成子树序列：因为我们希望剪枝前后误差最小，所以我们要寻找的就是最小α值对应的节点，把它剪掉。这时候生成了第一个子树。重复上面的过程，继续剪枝，直到最后只剩下根节点，即为最后一个子树。
• 验证：得到了剪枝后的子树集合后，我们需要用验证集对所有子树的误差计算一遍。可以通过计算每个子树的基尼指数或者平方误差，取误差最小的那个树，得到我们想要的结果。

总结

今天我给你讲了 CART 决策树，它是一棵决策二叉树，既可以做分类树，也可以做回归树。你需要记住的是，作为分类树，CART 采用基尼系数作为节点划分的依据，得到的是离散的结果，也就是分类结果；作为回归树，CART 可以采用最小绝对偏差（LAD），或者最小二乘偏差（LSD）作为节点划分的依据，得到的是连续值，即回归预测结果。

最后我们来整理下三种决策树之间在属性选择标准上的差异：

• ID3 算法，基于信息增益做判断；
• C4.5 算法，基于信息增益率做判断；
• CART 算法，分类树是基于基尼系数做判断。回归树是基于偏差做判断。

实际上这三个指标也是计算“不纯度”的三种计算方式。

在工具使用上，我们可以使用 sklearn 中的 DecisionTreeClassifier 创建 CART 分类树，通过 DecisionTreeRegressor 创建 CART 回归树。

你可以用代码自己跑一遍我在文稿中举到的例子。

思考题

最后给你留两道思考题吧，你能说下 ID3，C4.5，以及 CART 分类树在做节点划分时的区别吗？第二个问题是，sklearn 中有个手写数字数据集，调用的方法是 load_digits()，你能否创建一个 CART 分类树，对手写数字数据集做分类？另外选取一部分测试集，统计下分类树的准确率？

---

19丨决策树（下）：泰坦尼克乘客生存预测

sklearn 中的决策树模型

首先，我们需要掌握 sklearn 中自带的决策树分类器 DecisionTreeClassifier，方法如下：

clf = DecisionTreeClassifier(criterion='entropy')

到目前为止，sklearn 中只实现了 ID3 与 CART 决策树，所以我们暂时只能使用这两种决策树，在构造 DecisionTreeClassifier 类时，其中有一个参数是 criterion，意为标准。它决定了构造的分类树是采用 ID3 分类树，还是 CART 分类树，对应的取值分别是 entropy 或者 gini：

• entropy: 基于信息熵，也就是 ID3 算法，实际结果与 C4.5 相差不大；
• gini：默认参数，基于基尼系数。CART 算法是基于基尼系数做属性划分的，所以 criterion=gini 时，实际上执行的是 CART 算法。

我整理了这些参数代表的含义：

在构造决策树分类器后，我们可以使用 fit 方法让分类器进行拟合，使用 predict 方法对新数据进行预测，得到预测的分类结果，也可以使用 score 方法得到分类器的准确率。

下面这个表格是 fit 方法、predict 方法和 score 方法的作用。

Titanic 乘客生存预测

我们要对训练集中乘客的生存进行预测，这个过程可以划分为两个重要的阶段：

• 准备阶段：我们首先需要对训练集、测试集的数据进行探索，分析数据质量，并对数据进行清洗，然后通过特征选择对数据进行降维，方便后续分类运算；
• 分类阶段：首先通过训练集的特征矩阵、分类结果得到决策树分类器，然后将分类器应用于测试集。然后我们对决策树分类器的准确性进行分析，并对决策树模型进行可视化。

---

20丨朴素贝叶斯分类（上）：如何让机器判断男女？

求后验概率就是贝叶斯原理要求的

通用的贝叶斯公式

朴素贝叶斯

它是一种简单但极为强大的预测建模算法。

之所以称为朴素贝叶斯，是因为它假设每个输入变量是独立的。这是一个强硬的假设，实际情况并不一定，但是这项技术对于绝大部分的复杂问题仍然非常有效。

朴素贝叶斯模型由两种类型的概率组成：

• 每个类别的概率P(Cj)；

假设我有 7 个棋子，其中 3 个是白色的，4 个是黑色的。那么棋子是白色的概率就是 3/7，黑色的概率就是 4/7，这个就是类别概率。

• 每个属性的条件概率P(Ai|Cj)。

假设我把这 7 个棋子放到了两个盒子里，其中盒子 A 里面有 2 个白棋，2 个黑棋；盒子 B 里面有 1 个白棋，2 个黑棋。那么在盒子 A 中抓到白棋的概率就是 1/2，抓到黑棋的概率也是 1/2，这个就是条件概率，也就是在某个条件（比如在盒子 A 中）下的概率。

在朴素贝叶斯中，我们要统计的是属性的条件概率，也就是假设取出来的是白色的棋子，那么它属于盒子 A 的概率是 2/3。

为了训练朴素贝叶斯模型，我们需要先给出训练数据，以及这些数据对应的分类。那么上面这两个概率，也就是类别概率和条件概率。他们都可以从给出的训练数据中计算出来。一旦计算出来，概率模型就可以使用贝叶斯原理对新数据进行预测。

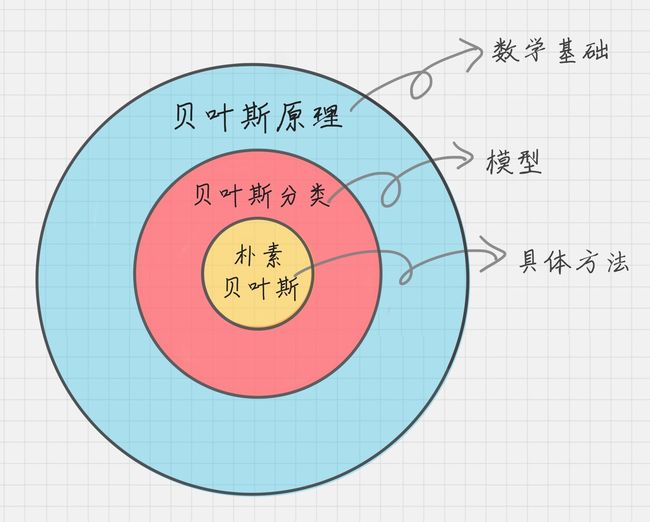
另外我想告诉你的是，贝叶斯原理、贝叶斯分类和朴素贝叶斯这三者之间是有区别的。

贝叶斯原理是最大的概念，它解决了概率论中“逆向概率”的问题，在这个理论基础上，人们设计出了贝叶斯分类器，朴素贝叶斯分类是贝叶斯分类器中的一种，也是最简单，最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的，因此对实际情况有所约束，如果属性之间存在关联，分类准确率会降低。不过好在对于大部分情况下，朴素贝叶斯的分类效果都不错。

朴素贝叶斯分类工作原理

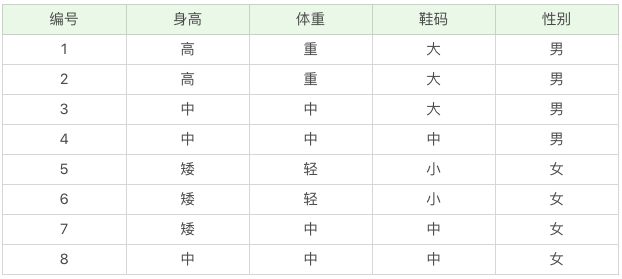
朴素贝叶斯分类是常用的贝叶斯分类方法。我们日常生活中看到一个陌生人，要做的第一件事情就是判断 TA 的性别，判断性别的过程就是一个分类的过程。根据以往的经验，我们通常会从身高、体重、鞋码、头发长短、服饰、声音等角度进行判断。这里的“经验”就是一个训练好的关于性别判断的模型，其训练数据是日常中遇到的各式各样的人，以及这些人实际的性别数据。

• 离散数据案例

针对这个问题，我们先确定一共有 3 个属性，假设我们用 A 代表属性，用 A1, A2, A3 分别为身高 = 高、体重 = 中、鞋码 = 中。一共有两个类别，假设用 C 代表类别，那么 C1,C2 分别是：男、女，在未知的情况下我们用 Cj 表示。

那么我们想求在 A1、A2、A3 属性下，Cj 的概率，用条件概率表示就是 P(Cj|A1A2A3)。根据上面讲的贝叶斯的公式，我们可以得出：

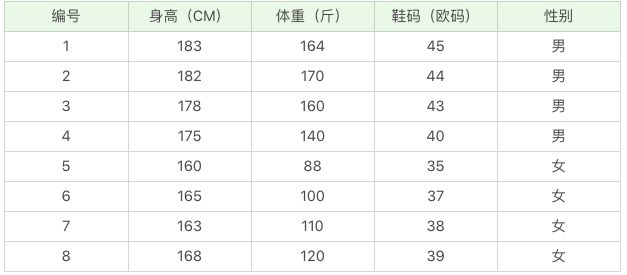
• 连续数据案例

那么如果给你一个新的数据，身高 180、体重 120，鞋码 41，请问该人是男是女呢？

这时，可以假设男性和女性的身高、体重、鞋码都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。比如，男性的身高是均值 179.5、标准差为 3.697 的正态分布。所以男性的身高为 180 的概率为 0.1069。怎么计算得出的呢? 你可以使用 EXCEL 的 NORMDIST(x,mean,standard_dev,cumulative) 函数，一共有 4 个参数：

• x：正态分布中，需要计算的数值；
• Mean：正态分布的平均值；
• Standard_dev：正态分布的标准差；
• Cumulative：取值为逻辑值，即 False 或 True。它决定了函数的形式。当为 TRUE 时，函数结果为累积分布；为 False 时，函数结果为概率密度。

朴素贝叶斯分类器工作流程

总结

思考题

第一道题，离散型变量和连续变量在朴素贝叶斯模型中的处理有什么差别呢？

答：离散变量可以直接求出概率，从而计算条件概率。连续变量需要假设密度函数（例如正态分布），然后通过带入值算出某一点的密度函数值。

第二个问题是，如果你的女朋友，在你的手机里发现了和别的女人的暧昧短信，于是她开始思考了 3 个概率问题，你来判断下下面的 3 个概率分别属于哪种概率：

• 你在没有任何情况下，出轨的概率；
• 如果你出轨了，那么你的手机里有暧昧短信的概率；
• 在你的手机里发现了暧昧短信，认为你出轨的概率。

这三种概率分别属于先验概率、后验概率和条件概率的哪一种？

答：

1、先验概率，以经验进行判断。
2、后验概率，以结果进行判断。
3、条件概率，在某种条件下，发生结果的概率。

---

21丨朴素贝叶斯分类（下）：如何对文档进行分类？

朴素贝叶斯分类最适合的场景就是文本分类、情感分析和垃圾邮件识别。其中情感分析和垃圾邮件识别都是通过文本来进行判断。从这里你能看出来，这三个场景本质上都是文本分类，这也是朴素贝叶斯最擅长的地方。所以朴素贝叶斯也常用于自然语言处理 NLP 的工具。

sklearn 机器学习包

sklearn 的全称叫 Scikit-learn，它给我们提供了 3 个朴素贝叶斯分类算法，分别是

• 高斯朴素贝叶斯（GaussianNB）
• 多项式朴素贝叶斯（MultinomialNB）
• 伯努利朴素贝叶斯（BernoulliNB）

这三种算法适合应用在不同的场景下，我们应该根据特征变量的不同选择不同的算法：

• 高斯朴素贝叶斯：特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。
• 多项式朴素贝叶斯：特征变量是离散变量，符合多项分布，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。
• 伯努利朴素贝叶斯：特征变量是布尔变量，符合 0/1 分布，在文档分类中特征是单词是否出现。

伯努利朴素贝叶斯是以文件为粒度，如果该单词在某文件中出现了即为 1，否则为 0。而多项式朴素贝叶斯是以单词为粒度，会计算在某个文件中的具体次数。而高斯朴素贝叶斯适合处理特征变量是连续变量，且符合正态分布（高斯分布）的情况。比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯。

什么是 TF-IDF 值呢？

TF-IDF 是一个统计方法，用来评估某个词语对于一个文件集或文档库中的其中一份文件的重要程度。

词频 TF：计算了一个单词在文档中出现的次数，它认为一个单词的重要性和它在文档中出现的次数呈正比。

逆向文档频率 IDF：指一个单词在文档中的区分度。它认为一个单词出现在的文档数越少，就越能通过这个单词把该文档和其他文档区分开。IDF 越大就代表该单词的区分度越大。

所以 TF-IDF 实际上是词频 TF 和逆向文档频率 IDF 的乘积。这样我们倾向于找到 TF 和 IDF 取值都高的单词作为区分，即这个单词在一个文档中出现的次数多，同时又很少出现在其他文档中。这样的单词适合用于分类。

TF-IDF 如何计算

为什么 IDF 的分母中，单词出现的文档数要加 1 呢？因为有些单词可能不会存在文档中，为了避免分母为 0，统一给单词出现的文档数都加 1。

TF-IDF=TF*IDF。

如何求 TF-IDF

在 sklearn 中我们直接使用 TfidfVectorizer 类，它可以帮我们计算单词 TF-IDF 向量的值。在这个类中，取 sklearn 计算的对数 log 时，底数是 e，不是 10。

什么是停用词？停用词就是在分类中没有用的词，这些词一般词频 TF 高，但是 IDF 很低，起不到分类的作用。为了节省空间和计算时间，我们把这些词作为停用词 stop words，告诉机器这些词不需要帮我计算。

如何对文档进行分类

• 基于分词的数据准备：包括分词、单词权重计算、去掉停用词；
• 应用朴素贝叶斯分类进行分类：首先通过训练集得到朴素贝叶斯分类器，然后将分类器应用于测试集，并与实际结果做对比，最终得到测试集的分类准确率。

数据挖掘神器 sklearn

从数据挖掘的流程来看，一般包括了获取数据、数据清洗、模型训练、模型评估和模型部署这几个过程。

sklearn 中包含了大量的数据挖掘算法，比如三种朴素贝叶斯算法，我们只需要了解不同算法的适用条件，以及创建时所需的参数，就可以用模型帮我们进行训练。在模型评估中，sklearn 提供了 metrics 包，帮我们对预测结果与实际结果进行评估。

在文档分类的项目中，我们针对文档的特点，给出了基于分词的准备流程。一般来说 NTLK 包适用于英文文档，而 jieba 适用于中文文档。我们可以根据文档选择不同的包，对文档提取分词。这些分词就是贝叶斯分类中最重要的特征属性。基于这些分词，我们得到分词的权重，即特征矩阵。

通过特征矩阵与分类结果，我们就可以创建出朴素贝叶斯分类器，然后用分类器进行预测，最后预测结果与实际结果做对比即可以得到分类器在测试集上的准确率。

总结

练习

文档共有 4 种类型：女性、体育、文学、校园；

训练集放到 train 文件夹里，测试集放到 test 文件夹里，停用词放到 stop 文件夹里。

请使用朴素贝叶斯分类对训练集进行训练，并对测试集进行验证，并给出测试集的准确率。

最后你不妨思考一下，假设我们要判断一个人的性别，是通过身高、体重、鞋码、外貌等属性进行判断的，如果我们用朴素贝叶斯做分类，适合使用哪种朴素贝叶斯分类器？停用词的作用又是什么？

---

22丨SVM（上）：如何用一根棍子将蓝红两色球分开？

SVM 的英文叫 Support Vector Machine，中文名为支持向量机。它是常见的一种分类方法，在机器学习中，SVM 是有监督的学习模型。

什么是有监督的学习模型呢？它指的是我们需要事先对数据打上分类标签，这样机器就知道这个数据属于哪个分类。

同样无监督学习，就是数据没有被打上分类标签，这可能是因为我们不具备先验的知识，或者打标签的成本很高。所以我们需要机器代我们部分完成这个工作，比如将数据进行聚类，方便后续人工对每个类进行分析。

SVM 作为有监督的学习模型，通常可以帮我们模式识别、分类以及回归分析。

练习 1：桌子上我放了红色和蓝色两种球，请你用一根棍子将这两种颜色的球分开。

你可以很快想到解决方案，在红色和蓝色球之间画条直线就好了

练习 2：这次难度升级，桌子上依然放着红色、蓝色两种球，但是它们的摆放不规律，如下图所示。如何用一根棍子把这两种颜色分开呢？

这里你可能会灵机一动，猛拍一下桌子，这些小球瞬间腾空而起。在腾起的那一刹那，出现了一个水平切面，恰好把红、蓝两种颜色的球分开。

在这里，二维平面变成了三维空间。原来的曲线变成了一个平面。这个平面，我们就叫做超平面。

升维

SVM 的工作原理

用 SVM 计算的过程就是帮我们找到那个超平面的过程，这个超平面就是我们的 SVM 分类器。

• 分类间隔

在保证决策面不变，且分类不产生错误的情况下，我们可以移动决策面 C，直到产生两个极限的位置：如图中的决策面 A 和决策面 B。极限的位置是指，如果越过了这个位置，就会产生分类错误。这样的话，两个极限位置 A 和 B 之间的分界线 C 就是最优决策面。极限位置到最优决策面 C 之间的距离，就是“分类间隔”，英文叫做 margin。

如果我们转动这个最优决策面，你会发现可能存在多个最优决策面，它们都能把数据集正确分开，这些最优决策面的分类间隔可能是不同的，而那个拥有“最大间隔”（max margin）的决策面就是 SVM 要找的最优解。

• 点到超平面的距离公式

超平面

在这个公式里，w、x 是 n 维空间里的向量，其中 x 是函数变量；w 是法向量。法向量这里指的是垂直于平面的直线所表示的向量，它决定了超平面的方向。

SVM 就是帮我们找到一个超平面，这个超平面能将不同的样本划分开，同时使得样本集中的点到这个分类超平面的最小距离（即分类间隔）最大化。

支持向量就是离分类超平面最近的样本点，实际上如果确定了支持向量也就确定了这个超平面。所以支持向量决定了分类间隔到底是多少，而在最大间隔以外的样本点，其实对分类都没有意义。

所以说， SVM 就是求解最大分类间隔的过程，我们还需要对分类间隔的大小进行定义。

首先，我们定义某类样本集到超平面的距离是这个样本集合内的样本到超平面的最短距离。我们用 di 代表点 xi 到超平面 wxi+b=0 的欧氏距离。因此我们要求 di 的最小值，用它来代表这个样本到超平面的最短距离。di 可以用公式计算得出：

其中||w||为超平面的范数。

最大间隔的优化模型

我们的目标就是找出所有分类间隔中最大的那个值对应的超平面。

硬间隔、软间隔和非线性 SVM

硬间隔指的就是完全分类准确，不能存在分类错误的情况。

软间隔，就是允许一定量的样本分类错误。

核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。

所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数，我们就可以把样本空间投射到新的高维空间中。

用 SVM 如何解决多分类问题

SVM 本身是一个二值分类器，最初是为二分类问题设计的，也就是回答 Yes 或者是 No。而实际上我们要解决的问题，可能是多分类的情况，比如对文本进行分类，或者对图像进行识别。

针对这种情况，我们可以将多个二分类器组合起来形成一个多分类器，常见的方法有“一对多法”和“一对一法”两种。

总结

今天我给你讲了 SVM 分类器，它在文本分类尤其是针对二分类任务性能卓越。同样，针对多分类的情况，我们可以采用一对多，或者一对一的方法，多个二值分类器组合成一个多分类器。

另外关于 SVM 分类器的概念，我希望你能掌握以下的三个程度：

• 完全线性可分情况下的线性分类器，也就是线性可分的情况，是最原始的 SVM，它最核心的思想就是找到最大的分类间隔；
• 大部分线性可分情况下的线性分类器，引入了软间隔的概念。软间隔，就是允许一定量的样本分类错误；
• 线性不可分情况下的非线性分类器，引入了核函数。它让原有的样本空间通过核函数投射到了一个高维的空间中，从而变得线性可分。

最后，你能说一下你对有监督学习和无监督学习的理解吗？以及，SVM 最主要的思想就是硬间隔、软间隔和核函数。你是如何理解它们的？

• 有监督学习，就是告诉他这个是红的那个是蓝的。你给我分出红蓝

• 无监督，自己学会认识红色和蓝色，然后再分类

• 硬间接，就是完美数据下的完美情况，分出完美类

• 软间隔，就是中间总有杂质，情况总是复杂，分类总是有一点错误

• 核函数，高纬度打低纬度，

---

23丨SVM（下）：如何进行乳腺癌检测？

在此之前我们先来回顾一下 SVM 的相关知识点。SVM 是有监督的学习模型，我们需要事先对数据打上分类标签，通过求解最大分类间隔来求解二分类问题。如果要求解多分类问题，可以将多个二分类器组合起来形成一个多分类器。

总结

SVM 整个执行的流程，包括数据加载、数据探索、数据清洗、特征选择、SVM 训练和结果评估等环节。

sklearn 已经为我们提供了很好的工具，对上节课中讲到的 SVM 的创建和训练都进行了封装，让我们无需关心中间的运算细节。但正因为这样，我们更需要对每个流程熟练掌握，通过实战项目训练数据化思维和对数据的敏感度。

---

24丨KNN（上）：如何根据打斗和接吻次数来划分电影类型？

KNN 的英文叫 K-Nearest Neighbor，应该算是数据挖掘算法中最简单的一种。

KNN 的工作原理

***近朱者赤，近墨者黑***可以说是 KNN 的工作原理。整个计算过程分为三步：

• 计算待分类物体与其他物体之间的距离；
• 统计距离最近的 K 个邻居；
• 对于 K 个最近的邻居，它们属于哪个分类最多，待分类物体就属于哪一类。

K 值如何选择

如果 K 值比较小，就相当于未分类物体与它的邻居非常接近才行。这样产生的一个问题就是，如果邻居点是个噪声点，那么未分类物体的分类也会产生误差，这样 KNN 分类就会产生过拟合。

如果 K 值比较大，相当于距离过远的点也会对未知物体的分类产生影响，虽然这种情况的好处是鲁棒性强，但是不足也很明显，会产生欠拟合情况，也就是没有把未分类物体真正分类出来。

所以 K 值应该是个实践出来的结果，并不是我们事先而定的。在工程上，我们一般采用交叉验证的方式选取 K 值。

交叉验证的思路就是，把样本集中的大部分样本作为训练集，剩余的小部分样本用于预测，来验证分类模型的准确性。所以在 KNN 算法中，我们一般会把 K 值选取在较小的范围内，同时在验证集上准确率最高的那一个最终确定作为 K 值。

距离如何计算

在 KNN 算法中，还有一个重要的计算就是关于距离的度量。两个样本点之间的距离代表了这两个样本之间的相似度。距离越大，差异性越大；距离越小，相似度越大。

关于距离的计算方式有下面五种方式：

• 欧氏距离；
• 曼哈顿距离；
• 闵可夫斯基距离；
• 切比雪夫距离；
• 余弦距离。

欧氏距离是我们最常用的距离公式，也叫做欧几里得距离。在二维空间中，两点的欧式距离就是：

同理，我们也可以求得两点在 n 维空间中的距离：

曼哈顿距离等于两个点在坐标系上绝对轴距总和。用公式表示就是：

闵可夫斯基距离不是一个距离，而是一组距离的定义。对于 n 维空间中的两个点 x(x1,x2,…,xn) 和 y(y1,y2,…,yn) ， x 和 y 两点之间的闵可夫斯基距离为：

其中 p 代表空间的维数，当 p=1 时，就是曼哈顿距离；当 p=2 时，就是欧氏距离；当 p→∞时，就是切比雪夫距离。

二个点之间的切比雪夫距离就是这两个点坐标数值差的绝对值的最大值，用数学表示就是：max(|x1-y1|,|x2-y2|)。

余弦距离实际上计算的是两个向量的夹角，是在方向上计算两者之间的差异，对绝对数值不敏感。在兴趣相关性比较上，角度关系比距离的绝对值更重要，因此余弦距离可以用于衡量用户对内容兴趣的区分度。比如我们用搜索引擎搜索某个关键词，它还会给你推荐其他的相关搜索，这些推荐的关键词就是采用余弦距离计算得出的。

KD 树

其实从上文你也能看出来，KNN 的计算过程是大量计算样本点之间的距离。为了减少计算距离次数，提升 KNN 的搜索效率，人们提出了 KD 树（K-Dimensional 的缩写）。KD 树是对数据点在 K 维空间中划分的一种数据结构。在 KD 树的构造中，每个节点都是 k 维数值点的二叉树。既然是二叉树，就可以采用二叉树的增删改查操作，这样就大大提升了搜索效率。

在这里，我们不需要对 KD 树的数学原理了解太多，你只需要知道它是一个二叉树的数据结构，方便存储 K 维空间的数据就可以了。而且在 sklearn 中，我们直接可以调用 KD 树，很方便。

用 KNN 做回归

KNN 不仅可以做分类，还可以做回归。

首先讲下什么是回归。在开头电影这个案例中，如果想要对未知电影进行类型划分，这是一个分类问题。首先看一下要分类的未知电影，离它最近的 K 部电影大多数属于哪个分类，这部电影就属于哪个分类。

如果是一部新电影，已知它是爱情片，想要知道它的打斗次数、接吻次数可能是多少，这就是一个回归问题。

那么 KNN 如何做回归呢？

对于一个新点，我们需要找出这个点的 K 个最近邻居，然后将这些邻居的属性的平均值赋给该点，就可以得到该点的属性。当然不同邻居的影响力权重可以设置成不同的。举个例子，比如一部电影 A，已知它是动作片，当 K=3 时，最近的 3 部电影是《战狼》，《红海行动》和《碟中谍 6》，那么它的打斗次数和接吻次数的预估值分别为 (100+95+105)/3=100 次、(5+3+31)/3=13 次。

总结

思考

最后我给你留几道思考题吧，KNN 的算法原理和工作流程是怎么样的？KNN 中的 K 值又是如何选择的？

答：

1、KNN的算法原理

离哪个邻居越近，属性与那个邻居越相似，和那个邻居的类别越一致。

2、KNN的工作流程

• 首先，根据场景，选取距离的计算方式
• 然后，统计与所需分类对象距离最近的K个邻居
• 最后，K个邻居中，所占数量最多的类别，即预测其为该分类对象的类别

3、K值的选取

交叉验证的方式，即设置多个测试集，用这些测试集测试多个K值，那个测试集所预测准确率越高的，即选取其相应的K值。

---

25丨KNN（下）：如何对手写数字进行识别？

今天我来带你进行 KNN 的实战。上节课，我讲了 KNN 实际上是计算待分类物体与其他物体之间的距离，然后通过统计最近的 K 个邻居的分类情况，来决定这个物体的分类情况。

如何用 KNN 对手写数字进行识别分类

手写数字数据集是个非常有名的用于图像识别的数据集。数字识别的过程就是将这些图片与分类结果 0-9 一一对应起来。完整的手写数字数据集 MNIST 里面包括了 60000 个训练样本，以及 10000 个测试样本。如果你学习深度学习的话，MNIST 基本上是你接触的第一个数据集。

今天我们用 sklearn 自带的手写数字数据集做 KNN 分类，你可以把这个数据集理解成一个简版的 MNIST 数据集，它只包括了 1797 幅数字图像，每幅图像大小是 8*8 像素。

KNN 分类的流程

• 数据加载：我们可以直接从 sklearn 中加载自带的手写数字数据集；
• 准备阶段：在这个阶段中，我们需要对数据集有个初步的了解，比如样本的个数、图像长什么样、识别结果是怎样的。你可以通过可视化的方式来查看图像的呈现。通过数据规范化可以让数据都在同一个数量级的维度。另外，因为训练集是图像，每幅图像是个 8*8 的矩阵，我们不需要对它进行特征选择，将全部的图像数据作为特征值矩阵即可；
• 分类阶段：通过训练可以得到分类器，然后用测试集进行准确率的计算。

总结

在数据量不大的情况下，使用 sklearn 还是方便的。

如果数据量很大，比如 MNIST 数据集中的 6 万个训练数据和 1 万个测试数据，那么采用深度学习 +GPU 运算的方式会更适合。因为深度学习的特点就是需要大量并行的重复计算，GPU 最擅长的就是做大量的并行计算。

---

26丨K-Means（上）：如何给20支亚洲球队做聚类？

总结

今天我给你讲了 K-Means 算法原理，我们再来看下开篇我给你提的三个问题。

如何确定 K 类的中心点？其中包括了初始的设置，以及中间迭代过程中中心点的计算。在初始设置中，会进行 n_init 次的选择，然后选择初始中心点效果最好的为初始值。在每次分类更新后，你都需要重新确认每一类的中心点，一般采用均值的方式进行确认。

如何将其他点划分到 K 类中？这里实际上是关于距离的定义，我们知道距离有多种定义的方式，在 K-Means 和 KNN 中，我们都可以采用欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离等。对于点的划分，就看它离哪个类的中心点的距离最近，就属于哪一类。

如何区分 K-Means 和 KNN 这两种算法呢？刚学过 K-Means 和 KNN 算法的同学应该能知道两者的区别，但往往过了一段时间，就容易混淆。所以我们可以从三个维度来区分 K-Means 和 KNN 这两个算法：

• 首先，这两个算法解决数据挖掘的两类问题。K-Means 是聚类算法，KNN 是分类算法。
• 这两个算法分别是两种不同的学习方式。K-Means 是非监督学习，也就是不需要事先给出分类标签，而 KNN 是有监督学习，需要我们给出训练数据的分类标识。
• 最后，K 值的含义不同。K-Means 中的 K 值代表 K 类。KNN 中的 K 值代表 K 个最接近的邻居。

两者的区别的比喻

K-means开班，选老大，风水轮流转，直到选出最佳中心老大

Knn小弟加队伍，离那个班相对近，就是那个班的

• Kmeans

一群人的有些人想要聚在一起；首先大家民主（无监督学习）随机选K个老大（随机选择K个中心点）；谁跟谁近，就是那个队伍的人（计算距离，距离近的聚合到一块）；随着时间的推移，老大的位置在变化（根据算法，重新计算中心点）；直到选出真正的中心老大（重复，直到准确率最高）

• Knn

一个人想要找到自己的队伍；首先听从神的旨意（有监督学习），随机最近的几个邻居；看看距离远不远（根据算法，计算距离）；近的就是一个班的了（属于哪个分类多，就是哪一类）

---

27丨K-Means（下）：如何使用K-Means对图像进行分割？

总结

---

28丨EM聚类（上）：如何将一份菜等分给两个人？

今天我来带你学习 EM 聚类。EM 的英文是 Expectation Maximization，所以 EM 算法也叫最大期望算法。

物以类聚，人已群分

例子

• 分菜
• 抛硬币

EM 聚类三步骤

你能从这个例子中看到三个主要的步骤：初始化参数、观察预期、重新估计。首先是先给每个碟子初始化一些菜量，然后再观察预期，这两个步骤实际上就是期望步骤（Expectation）。如果结果存在偏差就需要重新估计参数，这个就是最大化步骤（Maximization）。这两个步骤加起来也就是 EM 算法的过程。

EM 算法的工作原理

说到 EM 算法，我们先来看一个概念“最大似然”，英文是 Maximum Likelihood，Likelihood 代表可能性，所以最大似然也就是最大可能性的意思。

• 什么是最大似然呢？

举个例子，有一男一女两个同学，现在要对他俩进行身高的比较，谁会更高呢？根据我们的经验，相同年龄下男性的平均身高比女性的高一些，所以男同学高的可能性会很大。这里运用的就是最大似然的概念。

• 最大似然估计是什么呢？

它指的就是一件事情已经发生了，然后反推更有可能是什么因素造成的。还是用一男一女比较身高为例，假设有一个人比另一个人高，反推他可能是男性。最大似然估计是一种通过已知结果，估计参数的方法。

• 那么 EM 算法是什么？它和最大似然估计又有什么关系呢？

EM 算法是一种求解最大似然估计的方法，通过观测样本，来找出样本的模型参数。

简单总结下上面的步骤，你能看出 EM 算法中的 E 步骤就是通过旧的参数来计算隐藏变量。然后在 M 步骤中，通过得到的隐藏变量的结果来重新估计参数。直到参数不再发生变化，得到我们想要的结果。

EM 聚类的工作原理

上面你能看到 EM 算法最直接的应用就是求参数估计。如果我们把潜在类别当做隐藏变量，样本看做观察值，就可以把聚类问题转化为参数估计问题。这也就是 EM 聚类的原理。

总结

EM 算法相当于一个框架，你可以采用不同的模型来进行聚类，比如 GMM（高斯混合模型）或者 HMM（隐马尔科夫模型）来进行聚类。GMM 是通过概率密度来进行聚类，聚成的类符合高斯分布（正态分布）。而 HMM 用到了马尔可夫过程，在这个过程中，我们通过状态转移矩阵来计算状态转移的概率。HMM 在自然语言处理和语音识别领域中有广泛的应用。

在 EM 这个框架中，E 步骤相当于是通过初始化的参数来估计隐含变量。M 步骤就是通过隐含变量反推来优化参数。最后通过 EM 步骤的迭代得到模型参数。

通过上面举的炒菜的例子，你可以知道 EM 算法是一个不断观察和调整的过程。

通过求硬币正面概率的例子，你可以理解如何通过初始化参数来求隐含数据的过程，以及再通过求得的隐含数据来优化参数。

通过上面 GMM 图像聚类的例子，你可以知道很多 K-Means 解决不了的问题，EM 聚类是可以解决的。在 EM 框架中，我们将潜在类别当做隐藏变量，样本看做观察值，把聚类问题转化为参数估计问题，最终把样本进行聚类。

思考

用自己的话说一下 EM 算法的原理吗？EM 聚类和 K-Means 聚类的相同和不同之处又有哪些？

想起了一个故事，摘叶子：要找到最大的叶子

• 先心里大概有一个叶子大小的概念（初始化模型）
• 在三分之一的的路程上，观察叶子大小，并修改对大小的评估（观察预期，并修改参数）
• 在三分之二的路程上，验证自己对叶子大小模型的的评估（重复1,2过程）
• 在最后的路程上，选择最大的叶子（重复1.2，直到参数不再改变）

相同点

• EM，K-Means，都是随机生成预期值，然后经过反复调整，获得最佳结果
• 聚类个数清晰

不同点

• EM是计算概率，K-Means是计算距离
• 计算概率，概率只要不为0，都有可能即样本是每一个类别都有可能
• 计算距离，只有近的票高，才有可能，即样本只能属于一个类别

EM 就好像炒菜，做汤，盐多了放水，味淡了再放盐，直到合适为止。然后，就能得出放盐和水的比例（参数）

---

29丨EM聚类（下）：用EM算法对王者荣耀英雄进行划分

上节课，我讲了 EM 算法的原理，EM 算法相当于一个聚类框架，里面有不同的聚类模型，比如 GMM 高斯混合模型，或者 HMM 隐马尔科夫模型。其中你需要理解的是 EM 的两个步骤，E 步和 M 步：E 步相当于通过初始化的参数来估计隐含变量，M 步是通过隐含变量来反推优化参数。最后通过 EM 步骤的迭代得到最终的模型参数。

如何用 EM 算法对王者荣耀数据进行聚类

现在我们需要对王者荣耀的英雄数据进行聚类，我们先设定项目的执行流程：

总结

EM 聚类的实战，具体使用的是 GMM 高斯混合模型。从整个流程中可以看出，我们需要经过数据加载、数据探索、数据可视化、特征选择、GMM 聚类和结果分析等环节。

聚类和分类不一样，聚类是无监督的学习方式，也就是我们没有实际的结果可以进行比对，所以聚类的结果评估不像分类准确率一样直观，那么有没有聚类结果的评估方式呢？这里我们可以采用 Calinski-Harabaz 指标。

指标分数越高，代表聚类效果越好，也就是相同类中的差异性小，不同类之间的差异性大。当然具体聚类的结果含义，我们需要人工来分析，也就是当这些数据被分成不同的类别之后，具体每个类表代表的含义。

另外聚类算法也可以作为其他数据挖掘算法的预处理阶段，这样我们就可以将数据进行降维了。

---

30丨关联规则挖掘（上）：如何用Apriori发现用户购物规则？

关联规则挖掘可以让我们从数据集中发现项与项（item 与 item）之间的关系，它在我们的生活中有很多应用场景，“购物篮分析”就是一个常见的场景，这个场景可以从消费者交易记录中发掘商品与商品之间的关联关系，进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。所以说，关联规则挖掘是个非常有用的技术。

在今天的内容中，希望你能带着问题，和我一起来搞懂以下几个知识点：

• 搞懂关联规则中的几个重要概念：支持度、置信度、提升度；
• Apriori 算法的工作原理；
• 在实际工作中，我们该如何进行关联规则挖掘。

什么是支持度呢？

支持度是个百分比，它指的是某个商品组合出现的次数与总次数之间的比例。支持度越高，代表这个组合出现的频率越大。

什么是置信度呢？

它指的就是当你购买了商品 A，会有多大的概率购买商品 B。

所以说置信度是个条件概念，就是说在 A 发生的情况下，B 发生的概率是多少。

什么是提升度呢？

提升度 (A→B)= 置信度 (A→B)/ 支持度 (B)

这个公式是用来衡量 A 出现的情况下，是否会对 B 出现的概率有所提升。

所以提升度有三种可能：

• 提升度 (A→B)>1：代表有提升；
• 提升度 (A→B)=1：代表有没有提升，也没有下降；
• 提升度 (A→B)<1：代表有下降。

Apriori 的工作原理

Apriori 算法其实就是查找频繁项集 (frequent itemset) 的过程，所以首先我们需要定义什么是频繁项集。

频繁项集就是支持度大于等于最小支持度 (Min Support) 阈值的项集，所以小于最小值支持度的项目就是非频繁项集，而大于等于最小支持度的项集就是频繁项集。

到这里，你已经和我模拟了一遍整个 Apriori 算法的流程，下面我来给你总结下 Apriori 算法的递归流程：

• K=1，计算 K 项集的支持度；
• 筛选掉小于最小支持度的项集；
• 如果项集为空，则对应 K-1 项集的结果为最终结果。

否则 K=K+1，重复 1-3 步。

Apriori 的改进算法：FP-Growth 算法

• 可能产生大量的候选集。因为采用排列组合的方式，把可能的项集都组合出来了；
• 每次计算都需要重新扫描数据集，来计算每个项集的支持度。

所以 Apriori 算法会浪费很多计算空间和计算时间，为此人们提出了 FP-Growth 算法，它的特点是：

• 创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除，减少了存储空间。我稍后会讲解如何构造一棵 FP 树；
• 整个生成过程只遍历数据集 2 次，大大减少了计算量。

所以在实际工作中，我们常用 FP-Growth 来做频繁项集的挖掘，下面我给你简述下 FP-Growth 的原理。

• 创建项头表（item header table）

创建项头表的作用是为 FP 构建及频繁项集挖掘提供索引。

这一步的流程是先扫描一遍数据集，对于满足最小支持度的单个项（K=1 项集）按照支持度从高到低进行排序，这个过程中删除了不满足最小支持度的项。

项头表包括了项目、支持度，以及该项在 FP 树中的链表。初始的时候链表为空。

• 构造 FP 树

FP 树的根节点记为 NULL 节点。

整个流程是需要再次扫描数据集，对于每一条数据，按照支持度从高到低的顺序进行创建节点（也就是第一步中项头表中的排序结果），节点如果存在就将计数 count+1，如果不存在就进行创建。同时在创建的过程中，需要更新项头表的链表。

• 通过 FP 树挖掘频繁项集

到这里，我们就得到了一个存储频繁项集的 FP 树，以及一个项头表。我们可以通过项头表来挖掘出每个频繁项集。

具体的操作会用到一个概念，叫“条件模式基”，它指的是以要挖掘的节点为叶子节点，自底向上求出 FP 子树，然后将 FP 子树的祖先节点设置为叶子节点之和。

总结

今天我给你讲了 Apriori 算法，它是在“购物篮分析”中常用的关联规则挖掘算法，在 Apriori 算法中你最主要是需要明白支持度、置信度、提升度这几个概念，以及 Apriori 迭代计算频繁项集的工作流程。

Apriori 算法在实际工作中需要对数据集扫描多次，会消耗大量的计算时间，所以在 2000 年 FP-Growth 算法被提出来，它只需要扫描两次数据集即可以完成关联规则的挖掘。FP-Growth 算法最主要的贡献就是提出了 FP 树和项头表，通过 FP 树减少了频繁项集的存储以及计算时间。

当然 Apriori 的改进算法除了 FP-Growth 算法以外，还有 CBA 算法、GSP 算法，这里就不进行介绍。

---

31丨关联规则挖掘（下）：导演如何选择演员？

上次我给你讲了关联规则挖掘的原理。关联规则挖掘在生活中有很多使用场景，不仅是商品的捆绑销售，甚至在挑选演员决策上，你也能通过关联规则挖掘看出来某个导演选择演员的倾向。

今天我来带你用 Apriori 算法做一个项目实战。你需要掌握的是以下几点：

• 熟悉上节课讲到的几个重要概念：支持度、置信度和提升度；
• 熟悉与掌握 Apriori 工具包的使用；
• 在实际问题中，灵活运用。包括数据集的准备等。

如何使用 Apriori 工具包

$ pip install efficient-apriori

关于支持度、置信度和提升度，我们再来简单回忆下。

• 支持度指的是某个商品组合出现的次数与总次数之间的比例。支持度越高，代表这个组合出现的概率越大。
• 置信度是一个条件概念，就是在 A 发生的情况下，B 发生的概率是多少。
• 提升度代表的是“商品 A 的出现，对商品 B 的出现概率提升了多少”。

挖掘导演是如何选择演员的

• 在实际工作中，数据集是需要自己来准备的，比如今天我们要挖掘导演是如何选择演员的数据情况，但是并没有公开的数据集可以直接使用。因此我们需要使用之前讲到的 Python 爬虫进行数据采集。
• 有了数据之后，我们就可以用 Apriori 算法来挖掘频繁项集和关联规则

总结

Apriori 算法的核心就是理解频繁项集和关联规则。在算法运算的过程中，还要重点掌握对支持度、置信度和提升度的理解。在工具使用上，你可以使用 efficient-apriori 这个工具包，它会把每一条数据中的项（item）放到一个集合（篮子）里来处理，不考虑项（item）之间的先后顺序。

你认为 Apriori 算法中的最小支持度和最小置信度，一般设置为多少比较合理？

和数据集特点有关系，不过数据集大的情况下，不好观察特征。我们可以通过设置最小值支持度和最小置信度来观察关联规则的结果。

一般来说最小支持度常见的取值有0.5，0.1，0.05。最小置信度常见的取值有1.0，0.9，0.8。可以通过尝试一些取值，然后观察关联结果的方式来调整最小值尺度和最小置信度的取值。

---

32丨PageRank（上）：搞懂Google的PageRank算法

PageRank 的简化模型

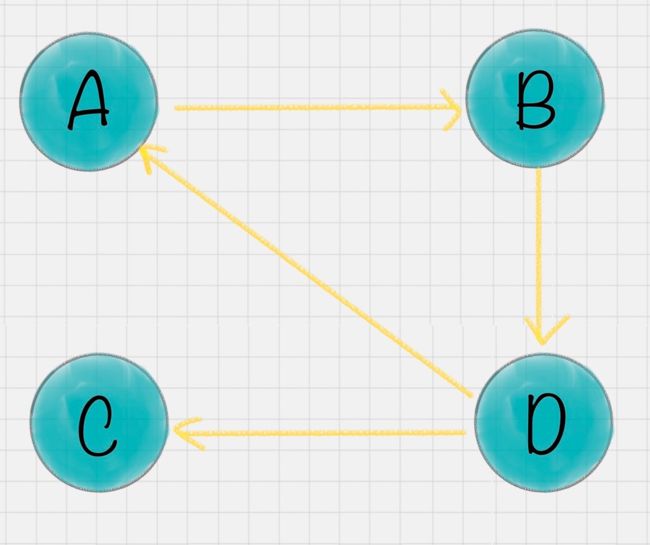
我假设一共有 4 个网页 A、B、C、D。它们之间的链接信息如图所示：

出链指的是链接出去的链接。入链指的是链接进来的链接。比如图中 A 有 2 个入链，3 个出链。

简单来说，一个网页的影响力 = 所有入链集合的页面的加权影响力之和，用公式表示为：

u 为待评估的页面，Bu 为页面 u 的入链集合。针对入链集合中的任意页面 v，它能给 u 带来的影响力是其自身的影响力 PR(v) 除以 v 页面的出链数量，即页面 v 把影响力 PR(v) 平均分配给了它的出链，这样统计所有能给 u 带来链接的页面 v，得到的总和就是网页 u 的影响力，即为 PR(u)。

所以你能看到，出链会给被链接的页面赋予影响力，当我们统计了一个网页链出去的数量，也就是统计了这个网页的跳转概率。

至此，我们模拟了一个简化的 PageRank 的计算过程，实际情况会比这个复杂，可能会面临两个问题：

• 等级泄露（Rank Leak）：如果一个网页没有出链，就像是一个黑洞一样，吸收了其他网页的影响力而不释放，最终会导致其他网页的 PR 值为 0。

• 等级沉没（Rank Sink）：如果一个网页只有出链，没有入链（如下图所示），计算的过程迭代下来，会导致这个网页的 PR 值为 0（也就是不存在公式中的 V）。

针对等级泄露和等级沉没的情况，我们需要灵活处理。

比如针对等级泄露的情况，我们可以把没有出链的节点，先从图中去掉，等计算完所有节点的 PR 值之后，再加上该节点进行计算。不过这种方法会导致新的等级泄露的节点的产生，所以工作量还是很大的。

有没有一种方法，可以同时解决等级泄露和等级沉没这两个问题呢？

PageRank 的随机浏览模型

为了解决简化模型中存在的等级泄露和等级沉没的问题，拉里·佩奇提出了 PageRank 的随机浏览模型。他假设了这样一个场景：用户并不都是按照跳转链接的方式来上网，还有一种可能是不论当前处于哪个页面，都有概率访问到其他任意的页面，比如说用户就是要直接输入网址访问其他页面，虽然这个概率比较小。

所以他定义了阻尼因子 d，这个因子代表了用户按照跳转链接来上网的概率，通常可以取一个固定值 0.85，而 1-d=0.15 则代表了用户不是通过跳转链接的方式来访问网页的，比如直接输入网址。

其中 N 为网页总数，这样我们又可以重新迭代网页的权重计算了，因为加入了阻尼因子 d，一定程度上解决了等级泄露和等级沉没的问题。

通过数学定理（这里不进行讲解）也可以证明，最终 PageRank 随机浏览模型是可以收敛的，也就是可以得到一个稳定正常的 PR 值。

PageRank 在社交影响力评估中的应用

• 微博影响力
• 职场影响力
• 企业经营能力

总结

今天我给你讲了 PageRank 的算法原理，对简化的 PageRank 模型进行了模拟。针对简化模型中存在的等级泄露和等级沉没这两个问题，PageRank 的随机浏览模型引入了阻尼因子 d 来解决。

同样，PageRank 有很广的应用领域，在许多网络结构中都有应用，比如计算一个人的微博影响力等。它也告诉我们，在社交网络中，链接的质量非常重要。

---

33丨PageRank（下）：分析希拉里邮件中的人物关系

在做一个关于 PageRank 算法的实战之前，你需要思考三个问题

• 如何使用工具完成 PageRank 算法，包括使用工具创建网络图，设置节点、边、权重等，并通过创建好的网络图计算节点的 PR 值；
• 对于一个实际的项目，比如希拉里的 9306 封邮件（工具包中邮件的数量），如何使用 PageRank 算法挖掘出有影响力的节点，并且绘制网络图；
• 如何对创建好的网络图进行可视化，如果网络中的节点数较多，如何筛选重要的节点进行可视化，从而得到精简的网络关系图。

如何使用工具实现 PageRank 算法

PageRank 算法工具在 sklearn 中并不存在，我们需要找到新的工具包。实际上有一个关于图论和网络建模的工具叫 NetworkX，它是用 Python 语言开发的工具，内置了常用的图与网络分析算法，可以方便我们进行网络数据分析。

上节课，我举了一个网页权重的例子，假设一共有 4 个网页 A、B、C、D，它们之间的链接信息如图所示：

针对这个例子，我们看下用 NetworkX 如何计算 A、B、C、D 四个网页的 PR 值，具体代码如下：

import networkx as nx
# 创建有向图
G = nx.DiGraph() 
# 有向图之间边的关系
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:
    G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=1)
print("pagerank 值是：", pagerank_list)

NetworkX 工具把中间的计算细节都已经封装起来了，我们直接调用 PageRank 函数就可以得到结果：

pagerank 值是： {'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}

我们通过 NetworkX 创建了一个有向图之后，设置了节点之间的边，然后使用 PageRank 函数就可以求得节点的 PR 值。

总结

在上节课中，我们通过矩阵乘法求得网页的权重，这节课我们使用 NetworkX 可以得到相同的结果。

另外我带你用 PageRank 算法做了一次实战，我们将一个复杂的网络图，通过 PR 值的计算、筛选，最终得到了一张精简的网络图。在这个过程中我们学习了 NetworkX 工具的使用，包括创建图、节点、边及 PR 值的计算。

实际上掌握了 PageRank 的理论之后，在实战中往往就是一行代码的事。但项目与理论不同，项目中涉及到的数据量比较大，你会花 80% 的时间（或 80% 的代码量）在预处理过程中，比如今天的项目中，我们对别名进行了统一，对边的权重进行计算，同时还需要把计算好的结果以可视化的方式呈现。

---

34丨AdaBoost（上）：如何使用AdaBoost提升分类器性能？

今天我们学习 AdaBoost 算法。在数据挖掘中，分类算法可以说是核心算法，其中 AdaBoost 算法与随机森林算法一样都属于分类算法中的集成算法。

集成算法的两种模式

集成的含义就是集思广益，博取众长，当我们做决定的时候，我们先听取多个专家的意见，再做决定。集成算法通常有两种方式，分别是投票选举（bagging）和再学习（boosting）。投票选举的场景类似把专家召集到一个会议桌前，当做一个决定的时候，让 K 个专家（K 个模型）分别进行分类，然后选择出现次数最多的那个类作为最终的分类结果。再学习相当于把 K 个专家（K 个分类器）进行加权融合，形成一个新的超级专家（强分类器），让这个超级专家做判断。

所以你能看出来，投票选举和再学习还是有区别的。Boosting 的含义是提升，它的作用是每一次训练的时候都对上一次的训练进行改进提升，在训练的过程中这 K 个“专家”之间是有依赖性的，当引入第 K 个“专家”（第 K 个分类器）的时候，实际上是对前 K-1 个专家的优化。而 bagging 在做投票选举的时候可以并行计算，也就是 K 个“专家”在做判断的时候是相互独立的，不存在依赖性。

AdaBoost 的工作原理

AdaBoost 的英文全称是 Adaptive Boosting，中文含义是自适应提升算法

什么是 Boosting 算法呢？Boosting 算法是集成算法中的一种，同时也是一类算法的总称。这类算法通过训练多个弱分类器，将它们组合成一个强分类器，也就是我们俗话说的“三个臭皮匠，顶个诸葛亮”。

我可以用上面的图来表示最终得到的强分类器，你能看出它是通过一系列的弱分类器根据不同的权重组合而成的。

假设弱分类器为 Gi(x)，它在强分类器中的权重 αi，那么就可以得出强分类器 f(x)：

有了这个公式，为了求解强分类器，你会关注两个问题：

• 如何得到弱分类器，也就是在每次迭代训练的过程中，如何得到最优弱分类器？

实际上，AdaBoost 算法是通过改变样本的数据分布来实现的。AdaBoost 会判断每次训练的样本是否正确分类，对于正确分类的样本，降低它的权重，对于被错误分类的样本，增加它的权重。再基于上一次得到的分类准确率，来确定这次训练样本中每个样本的权重。然后将修改过权重的新数据集传递给下一层的分类器进行训练。这样做的好处就是，通过每一轮训练样本的动态权重，可以让训练的焦点集中到难分类的样本上，最终得到的弱分类器的组合更容易得到更高的分类准确率。

• 每个弱分类器在强分类器中的权重是如何计算的？

实际上在一个由 K 个弱分类器中组成的强分类器中，如果弱分类器的分类效果好，那么权重应该比较大，如果弱分类器的分类效果一般，权重应该降低。所以我们需要基于这个弱分类器对样本的分类错误率来决定它的权重，用公式表示就是：

其中 ei 代表第 i 个分类器的分类错误率。

总结

今天我给你讲了 AdaBoost 算法的原理，你可以把它理解为一种集成算法，通过训练不同的弱分类器，将这些弱分类器集成起来形成一个强分类器。在每一轮的训练中都会加入一个新的弱分类器，直到达到足够低的错误率或者达到指定的最大迭代次数为止。实际上每一次迭代都会引入一个新的弱分类器（这个分类器是每一次迭代中计算出来的，是新的分类器，不是事先准备好的）。

在弱分类器的集合中，你不必担心弱分类器太弱了。实际上它只需要比随机猜测的效果略好一些即可。如果随机猜测的准确率是 50% 的话，那么每个弱分类器的准确率只要大于 50% 就可用。AdaBoost 的强大在于迭代训练的机制，这样通过 K 个“臭皮匠”的组合也可以得到一个“诸葛亮”（强分类器）。

当然在每一轮的训练中，我们都需要从众多“臭皮匠”中选择一个拔尖的，也就是这一轮训练评比中的最优“臭皮匠”，对应的就是错误率最低的分类器。当然每一轮的样本的权重都会发生变化，这样做的目的是为了让之前错误分类的样本得到更多概率的重复训练机会。

同样的原理在我们的学习生活中也经常出现，比如善于利用错题本来提升学习效率和学习成绩。

---

35丨AdaBoost（下）：如何使用AdaBoost对房价进行预测？

我们先做个简单回忆，什么是分类，什么是回归呢？

实际上分类和回归的本质是一样的，都是对未知事物做预测。不同之处在于输出结果的类型，分类输出的是一个离散值，因为物体的分类数有限的，而回归输出的是连续值，也就是在一个区间范围内任何取值都有可能。

目标

这次我们的主要目标是使用 AdaBoost 预测房价，这是一个回归问题。除了对项目进行编码实战外，我希望你能掌握：

• AdaBoost 工具的使用，包括使用 AdaBoost 进行分类，以及回归分析。
• 使用其他的回归工具，比如决策树回归，对比 AdaBoost 回归和决策树回归的结果。

总结

用 AdaBoost 回归分析对波士顿房价进行了预测。因为这是个回归分析的问题，我们直接使用 sklearn 中的 AdaBoostRegressor 即可。如果是分类，我们使用 AdaBoostClassifier。

另外我们将 AdaBoost 分类器、弱分类器和决策树分类器做了对比，可以看出经过多个弱分类器组合形成的 AdaBoost 强分类器，准确率要明显高于决策树算法。所以 AdaBoost 的优势在于框架本身，它通过一种迭代机制让原本性能不强的分类器组合起来，形成一个强分类器。

其实在现实工作中，我们也能找到类似的案例。IBM 服务器追求的是单个服务器性能的强大，比如打造超级服务器。而 Google 在创建集群的时候，利用了很多 PC 级的服务器，将它们组成集群，整体性能远比一个超级服务器的性能强大。

再比如我们讲的“三个臭皮匠，顶个诸葛亮”，也就是 AdaBoost 的价值所在。

思考

今天我们用 AdaBoost 分类器与决策树分类做对比的时候，使用到了 sklearn 中的 make_hastie_10_2 函数生成数据。实际上在第 19 篇，我们对泰坦尼克号的乘客做生存预测的时候，也讲到了决策树工具的使用。你能不能编写代码，使用 AdaBoost 算法对泰坦尼克号乘客的生存做预测，看看它和决策树模型，谁的准确率更高？

---

36丨数据分析算法篇答疑

决策树

• 答疑 1：在探索数据的代码中，print(boston.feature_names) 有什么作用？
• 答疑 2：决策树的剪枝在 sklearn 中是如何实现的？
• 答疑 3：对泰坦尼克号的乘客做生存预测的时候，Carbin 字段缺失率分别为 77% 和 78%，Age 和 Fare 字段有缺失值，是如何判断出来的？
• 答疑 4：在用 pd.read_csv 时报错“UnicodeDecodeError utf-8 codec can’t decode byte 0xcf in position 15: invalid continuation byte”是什么问题？

朴素贝叶斯

• 答疑 1：在朴素贝叶斯中，我们要统计的是属性的条件概率，也就是假设取出来的是白色的棋子，那么它属于盒子 A 的概率是 2/3。这个我算的是 3/5，跟老师的不一样，老师可以给一下详细步骤吗？

SVM 算法

• 答疑 1：SVM 多分类器是集成算法么？

K-Means

• 答疑 1：我在给 20 支亚洲球队做聚类模拟的时候，使用 K-Means 算法需要重新计算这三个类的中心点，最简单的方式就是取平均值，然后根据新的中心点按照距离远近重新分配球队的分类。对中心点的重新计算不太理解。

EM 聚类

• 答疑 1：关于 EM 聚类初始参数设置的问题，初始参数随机设置会影响聚类的效果吗。会不会初始参数不对，聚类就出错了呢？

关联规则挖掘

• 答疑 1：看不懂构造 FP 树的过程，面包和啤酒为什么会拆分呢？
• 答疑 2：不怎么会找元素的 XPath 路径。
• 答疑 3：最小支持度可以设置小一些，如果最小支持度小，那么置信度就要设置得相对大一点，不然即使提升度高，也有可能是巧合。这个参数跟数据量以及项的数量有关。理解对吗？

AdaBoost 算法

• 答疑 1：关于 Zk 和 yi 的含义