数学建模重要算法简介及算法实现
一.蒙特卡洛算法
1,定义:蒙特卡洛算法是以概率和统计的理论、方法为基础的一种数值计算方法,将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解,故又称随机抽样法或统计实验法。
2.适用范围:可以较好的解决多重积分计算、微分方程求解、积分方程求解、特征值计算和非线性方程组求解等高难度和复杂的数学计算问题。
3.特点:蒙特卡洛算法可以应用在很多场合,但求的是近似解,在模拟样本越大的情况下,越接近于真实值,单样本数增加会带来计算量的大幅上升。对于一些简单问题来说,蒙特卡洛是个笨办法,但对于许多问题来说,它往往是个有效,有时甚至是唯一可行的方法。
4.代码:具体问题参考博文https://blog.csdn.net/u013414501/article/details/50478898
matlab代码
%作图的代码
x = 0:0.25:12;
y1 = x.^2;
y2 = 12 - x;
plot(x, y1, x, y2)
xlabel('x');ylabel('y');
%产生图例
legend('y1=x^2', 'y2=12-x');
title('马驰绘制');
%图中x轴和y轴的范围,中括号前面是y轴范围,中括号后面是x轴范围
axis([0 15 0 15]);
text(3, 9, '交点');
%画图时加上网格线
grid on
%蒙特卡洛算法的具体实现
%产生一个1行10000000列的矩阵,矩阵中每个数是从0到12之间随机取
x = unifrnd(0, 12, [1, 10000000]);
y = unifrnd(0, 9, [1, 10000000]);
frequency = sum(y=3);
area = 12*9*frequency/10^7;
disp(area); 关于matlab中的unifrnd函数可以参考博文https://blog.csdn.net/LucyLiHHU/article/details/78568741
上述代码是求一重积分的例子
二.数据拟合
1.定义:不要求近似函数通过所有的数据点,而是要求他能较好的反应数据的整体变化趋势。
2.常用方法:最小二乘拟合方法
3.代码:具体问题参考博文https://blog.csdn.net/sunboyiris/article/details/17222279
matlab代码
%读取表格
A = xlsread('E:\表格\1.xls', 'Sheet1', 'A1:AN2');
B = A;
[I, J] = size(B);
%数据拟合
%x为矩阵的第一行,y为矩阵的第二行
x = A(1,:);
y = A(2,:);
%polyfit为matlab中的拟合函数,第一个参数是数据的横坐标
%第二个参数是数据的纵坐标,第三个参数是多项式的最高阶数
%返回值p中包含n+1个多项式系数
p = polyfit(x, y, 2);
disp(p);
%下面是作图的代码
x1 = 300:10:600;
%polyval是matlab中的求值函数,求x1对应的函数值y1
y1 = polyval(p,x1);
plot(x,y,'*r',x1,y1,'-b');
%plot(x,'DisplayName','x','YDataSource','x');
%figure(gcf);
使用matlab的图形化拟合包(推荐)
(1)将数据导入工作区并通过cftool命令打开matlab的图形化拟合包
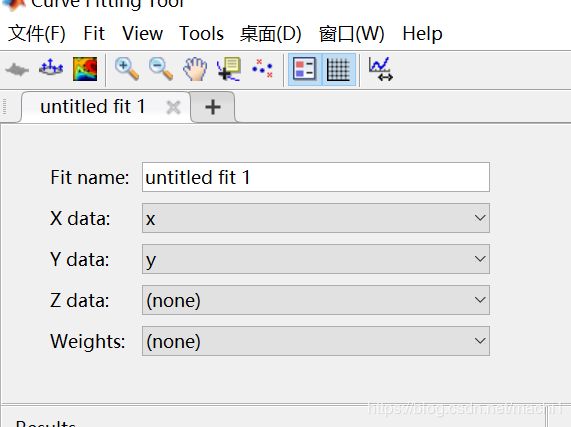
(2)选择x、y变量
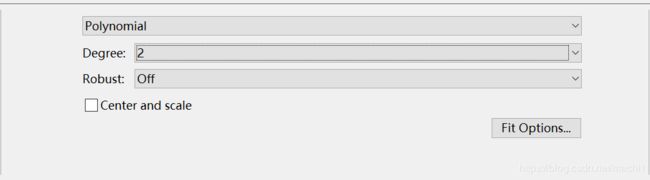
(3)选择拟合方式和最高项次数
(4)得到拟合结果
使用图形化拟合工具不仅简单快捷,还可以使用多种拟合方式,寻找到最好的拟合曲线。
三.参数估计
1.定义:参数估计是统计推断的一种。根据从总体中抽取的随机样本来估计总体分布中未知参数的过程。
2.标准特点:无偏性、有效性、一致性。
3.主要分类:点估计和区间估计。
4.要处理的问题:求出未知参数的估计量和在一定信度下指出所求的估计量的精度。
5.代码:这里未找到关于参数估计相关的代码,感觉对于这种计算可能需要根据具体题目进行计算。相关的计算方法在概率论中都已经学习过了。
四.插值
1.定义:在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。
2.作用:插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值情况,估算出函数在其他点处的近似值。
3.区别:从定义上看,插值和拟合有一定的相似度,但插值要求近似函数通过给定的所有离散数据,而拟合并不要求这样,只要近似函数能较好的反映数据变化的趋势即可(近似含义不同),当测量值是准确的,没有误差时,一般用插值;当测量值与真实值有误差时,一般用数据拟合。
4.代码
matlab代码
%years、service和wage是原始数据
years = 1950:10:1990;
service = 10:10:30;
wage = [ 150.697 199.592 187.625 179.323 195.072; 250.287 203.212 179.092 322.767 226.505;153.706 426.730 249.633 120.281 598.243];
[X, Y] = meshgrid(years, service);
% % 三维曲线
% plot3(X, Y, wage)
% 三维曲面
figure
surf(X, Y, wage)
%interp2是matlab中的二维插值函数,前两个参数是已知未知,后两个是未知位置,w是未知位置的插值结果
w = interp2(service,years,wage,15,1975);
五.线性规划
1.定义:线性规划是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
2.步骤:
(1)根据影响所要达到目的的因素找到决策变量。
(2)由决策变量和所在达到目的之间的函数关系确定目标函数。
(3)由决策变量所受的限制条件确定决策变量所要满足的约束条件。
3.特点:目标函数是决策变量的线性函数。根据具体问题可以是最大化或最小化,二者统称为最优化。约束条件也是决策变量的线性函数。
4.代码
Lingo代码(具体的Lingo语法可以参考博文:https://blog.csdn.net/machi1/article/details/98517125)
model:
min = 2*x1 + 3*x2;
x1 + x2 >= 350;
x1 >= 100;
2*x1 + x2 <= 600;
end
六.整数规划
1.定义:整数规划是指规划中的变量(全部或部分)限制为整数,若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。
2.分类:在整数规划中,如果所有变量都限制为整数,则称为纯整数规划;如果仅一部分限制为整数,则称为混合整数规划。整数规划的一种特殊情形是0-1规划,它的变数仅限于0或1。
3.0-1规z划:问题中许多量具有不可分割的性质(最优调度的车辆数、设置的销售网点数......),或者问题的解必须满足一些特殊的约束条件(满足逻辑条件、顺序.....),需引入逻辑变量(0-1变量)以表示“是”与“非”。这类问题的模型均为整数规划。
4.代码
Lingo实现整数规划(一般的整数规划)
model:
min = 2*x1 + 3*x2;
x1 + x2 >= 350;
x1 >= 100;
2*x1 + x2 <= 600;
!@gin(变量)表示该变量只能取整数;
@gin(x1);
@gin(x2);
endLingo实现0-1规划
model:
max = 2*x1 + 5*x2 + 3*x3 + 4*x4;
-4*x1 + x2 + x3 + x4 >= 0;
-2*x1 + 4*x2 + 2*x3 + 4*x4 >= 1;
x1 + x2 - x3 + x4 >= 1;
!@bin(变量)限定变量只能取0或1
@bin(x1);
@bin(x2);
@bin(x3);
@bin(x4);
end
七.多目标线性规划
1.定义:在相同的条件下,要求多个目标函数都得到最好的满足,这便是多目标规划。若目标函数和约束条件都是线性的,则为多目标线性规划。
2.求解方法:
(1)化多为少的方法,即把多目标华为比较容易求解的单目标或双目标,如主要目标法、线性加权法、理想点法等。
(2)分层序列法,即把目标按其重要性给出一个序列,每次都在前一个目标最优解集内求下一个目标最优解,知道求出共同的最优解。
(3)层次分析法,这是一种定性与定量相结合的多目标决策与分析方法,对于目标结构复杂且缺乏必要的数据的情况更为实用。
3.代码:由于解多目标规划问题比较困难,等之后看懂了会更新这部分的代码。
先放一个链接:https://blog.csdn.net/wzl1997/article/details/79120323
八.二次规划
1.定义:二次规划是非线性规划中的一类特殊数学规划问题,在很多方面都有应用,如投资组合、约束最小二乘问题的求解、序列二次规划在非线性优化问题中应用等。
2.特点:目标函数是二次的,并且约束是线性的问题。在非线性约束最优化问题中非常重要,通常作为其他问题的子步骤存在。
九.最优化方法
1.定义:最优化方法,是指解决最优化问题的方法。所谓最优化问题,指在某些约束条件下,决定某些可选择的变量应该取何值,使所选定的目标函数达到最优的问题。即运用最新科技手段和处理方法,使系统达到总体最优。
2.数学意义:最优化方法是一种求极值的方法,即在一组约束为等式或不等式的条件下,使系统的目标函数达到极值,即最大值或最小值。
3.基本要素:最优化模型一般包括变量、约束条件和目标函数三要素。
4.无约束优化:
(1)在数值优化中,一般采用迭代法求解无约束优化问题。
(2)无约束优化的算法框架
(3)关键问题:搜索方向、终止条件、步长
(4)线搜索技术:通过公式求出每次迭代的步长,分为精确线搜索和非精确线搜索。
(5)Armijo准则(非精确线搜索的准则)
5.无约束优化算法
(1)牛顿法(参考博文:https://blog.csdn.net/qq_28743951/article/details/82221515)
原始的牛顿迭代法的缺点:
1)初值点选择(敏感):基本牛顿法初始点需要足够靠近极小点,否则有可能导致算法不收敛。
2)Hessen矩阵正定
代码:
function [x, val, k] = niudun1(x0)
%基本牛顿法求函数最小值
%x是最小值点,val是最小值,k是迭代次数
epsilon = 1e-5; %终止误差值
k = 0; %迭代次数
%如果梯度的范数小于终止误差值则停止迭代
while norm(g(x0)) > epsilon
d = -G(x0)\g(x0);
x0 = x0 + d';
k = k+1;
end
x = x0;
val = f(x0);
end
%%原函数
function y = f(x)
y = 100*(x(1)^2 - x(2))^2 + (x(1) - 1)^2;
end
%%原函数的梯度,要弄成列向量的形式
function y = g(x)
y(1,1) = 400*x(1)*(x(1)^2 - x(2)) + 2*(x(1) - 1);
y(2,1) = -200*(x(1)^2 - x(2));
end
%%原函数的Hessen矩阵,注意矩阵每个元素的值
function y = G(x)
y(1, 1) = 1200*x(1)^2 - 400*x(2) + 2;
y(1, 2) = -400*x(1);
y(2, 1) = -400*x(1);
y(2, 2) = 200;
end
(2)阻尼牛顿法(参考博文:https://blog.csdn.net/philosophyatmath/article/details/70153705)
优点:阻尼牛顿法在基本牛顿法的基础上增加对步长的线搜索,克服了基本牛顿法对于初始点敏感的问题。
算法:
代码:(对于x0要输入列向量)
function [x,val,k]=damp_Newton(fun,gfun, Hess,x0)
%功能: 用阻尼牛顿法求解无约束问题: min f(x)
%输入: x0是初始点, fun, gfun, Hess 分别是求
% 目标函数,梯度,Hesse 阵的函数
%输出: x, val分别是近似最优点和最优值, k是迭代次数.
maxk=10000; %给出最大迭代次数
rho=0.55;sigma=0.5;
k=0; epsilon=1e-5;
tic
while(k(3)最速下降法
优点:最速下降法只需要求函数的梯度,并不需要求函数的Hessen矩阵,而且最速梯度法对于初始值的选取并不敏感,全局收敛。
缺点:迭代速度较慢。
算法(参考博文:https://baike.baidu.com/item/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D/4864937?fromtitle=%E6%9C%80%E9%80%9F%E4%B8%8B%E9%99%8D%E6%B3%95&fromid=7186948&fr=aladdin)
代码:
function [x, val, k] = zuisuxiajiang(x0)
%使用最速下降法求解最小值
%x是迭代后的最小值点,val是最小值,k是迭代次数
%x0是初始值,最速下降法对于初始值不敏感
k = 0;
epsilon = 1e-10; %终止误差值
%rho和sigma是线搜索法的两个参数
rho = 0.55;
sigma = 0.5;
%当函数梯度的范数小于等于终止误差值时停止迭代
while norm(g(x0)) > epsilon
d = -g(x0);
m = 0;
while (f(x0 + rho^m*d) > (f(x0)+sigma*rho^m*g(x0)'*d))
m = m + 1;
end
x0 = x0 + rho^m*d;
k = k + 1;
end
x = x0;
val = f(x0);
end
%%原函数
function y = f(x)
y = 100*(x(1)^2 - x(2))^2 + (x(1) - 1)^2;
end
%%原函数的梯度,要弄成列向量的形式
function y = g(x)
y(1,1) = 400*x(1)*(x(1)^2 - x(2)) + 2*(x(1) - 1);
y(2,1) = -200*(x(1)^2 - x(2));
end
%%原函数的Hessen矩阵,注意矩阵每个元素的值
function y = G(x)
y(1, 1) = 1200*x(1)^2 - 400*x(2) + 2;
y(1, 2) = -400*x(1);
y(2, 1) = -400*x(1);
y(2, 2) = 200;
end(4)信赖域方法
优点:信赖域方法是一种保证全局收敛的优化算法,并且可以直接确定位移,产生新的迭代点。
思想:(求出位移,并根据位移的相关信息调整信赖域半径)
算法:
代码:
function [xk,val,k]=trustm(x0)
%功能: 牛顿型信赖域方法求解无约束优化问题 min f(x)
%输入: x0是初始迭代点
%输出: xk是近似极小点, val是近似极小值, k是迭代次数
n=length(x0); x=x0; dta=1;
eta1=0.15; eta2=0.75; dtabar=2.0;
tau1=0.5; tau2=2.0; epsilon=1e-6;
k=0; Bk=Hess(x); %Bk=eye(n);
while(k<150)
gk=gfun(x); %%%% 梯度值
if(norm(gk)=eta2&norm(d)==dta)
dta=min(tau2*dta,dtabar); %%%%放大
else
dta=dta; %%%维持不动
end
end
if(rk>eta1)
x0=x; x=x+d; %%%产生新的迭代点
% sk=x-x0; yk=gfun(x)-gfun(x0);
%vk=sqrt(yk'*Bk*yk)*(sk/(sk'*yk)-Bk*yk/(yk'*Bk*yk));
%Bk=Bk-Bk*yk*yk'*Bk/(yk'*Bk*yk)+sk*sk'/(sk'*yk)+vk*vk'
%pause
Bk=Hess(x);
end
k=k+1;
end
xk=x;
val=fun(xk);
%%% 目标函数 %%%%%%%%%%%%%%%
function f=fun(x)
f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;
%%% 子问题目标函数 %%%%%%%%%%%%%
function qd=qk(x,d)
gk=gfun(x); Bk=Hess(x);
qd=gk'*d+0.5*d'*Bk*d;
%%% 目标函数的梯度 %%%%%%%%%%%%%%
function gf=gfun(x)
gf=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1), -200*(x(1)^2-x(2))]';
%%% 目标函数的Hesse阵 %%%%%%%%%%%%%%
function He=Hess(x)
n=length(x);
He=zeros(n,n);
He=[1200*x(1)^2-400*x(2)+2, -400*x(1);
-400*x(1), 200 ];
6.有约束优化算法
1)带约束的非线性规划问题的常用解法是制约函数法,其基本思想是:将求解非线性规划问题转化为一系列无约束的极值问题来求解,故此方法也称为序列无约束最小化方法。在无约束问题的求解过程中,对企图违反约束的那些点给出相应的惩罚约束,迫使这一系列的无约束问题的极小点不断地向可行域靠近(若在可行域外部),或者一直在可行域内移动(若在可行域内部),直到收敛到原问题地最优解为止。
2)常用的制约函数可分为两类:惩罚函数(简称罚函数)和障碍函数。从方法来讲分为外点法(或外部惩罚函数法)和内点法(或内部惩罚函数法,即障碍函数法)。
十.线性回归
1.定义:线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,运用十分广泛。其表达式形式为y=w'x+e,e为误差服从均值为0的正态分布。
2.分类:回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
3.作用:
(1)如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出以一个y值。(例如:主成分分析法、层次分析法等)
(2)给定一个变量y和一些变量X,这些变量有可能与y相关,线性回归分析可以用来量化y和X之间相关性的强度,评估出与y不相关的X,并识别出哪些X的子集包含了y的冗余信息。
十一.图论与网络优化
1.最短路问题:怎样才能选择一条距离最短的路线。实际上是一个0-1规划问题。
2.最大运量的运输问题:选择一条从源点到汇点容量最大的路线。实际上是一个线性(或非线性)规划问题。
3.最大流问题:从源点到经过的所有路径的最终到达汇点的所有流量和最大。是一个特殊的线性规划问题。(参考博文:https://www.cnblogs.com/zsboy/archive/2013/01/27/2878810.html)
4.旅行商问题:寻找一条经过所有顶点,并回到原点的最短路。这是一个特殊的0-1规划问题。
5.最优连线问题:在保证各城市连通的前提下,希望修建的总长度最短。在图论中称为最小生成树的问题。
6.以上关于图论的问题都可以使用lingo求解。
十二.排队论
1.定义:排队论或称随机服务系统理论,是通过对服务对象到来及服务时间的统计研究,得出这些数量指标(等待时间、排队长度、忙期长短等)的统计规律,然后根据这些规律来改进服务系统的结构或重新组织被服务对象,使得服务系统既能满足服务对象的需要,又能使机构的费用最经济或某些指标最优。
2.研究内容:
(1)性态问题:排队系统的概率分布规律。
(2)最优化问题:分为静态最优化和动态最优化。
(3)排队系统的统计推断:判断一个给定的排队系统符合哪种模型。
3.排队模型的表示
X/Y/Z/A/B/C
X—顾客相继到达的间隔时间的分布;
Y—服务时间的分布;
M—负指数分布、D—确定型、Ek —k阶爱尔兰分布;
Z—服务台个数;
A—系统容量限制(默认为∞);
B—顾客源数目(默认为∞);
C—服务规则 (默认为先到先服务FCFS)。
4.评价一个排队系统的好坏要以顾客与服务机构两方面的利益为标准。就顾客来说总希望等待时间或逗留时间越短越好,从而希望服务台个数尽可能多些但是,就服务机构来说,增加服务台数,就意味着增加投资,增加多了会造成浪费,增加少了要引起顾客的抱怨甚至失去顾客,增加多少比较好呢?顾客与服务机构为了照顾自己的利益对排队系统中的3个指标:队长、等待时间、服务台的忙期(简称忙期)都很关心。因此这3个指标也就成了排队论的主要研究内容。
5.排队论的应用非常广泛。它适用于一切服务系统。尤其在通信系统、交通系统、计算机、存贮系统、生产管理系统等方面应用得最多。排队论的产生与发展来自实际的需要,实际的需要也必将影响它今后的发展方向。
6.参考博文:https://blog.csdn.net/sunyueqinghit/article/details/81562138
十三. 对策论方法(博弈论)
1.对策论是运筹学的一个重要分支,它所研究的典型问题是两个或两个以上的参加者在某种对抗性或竞争性的场合下各自做出决策,使自己的一方得到最有利的结果。
2.在对策论中,总是假设每个局中人都是“理智的”,即竞争者是公平理智的竞争。
3.局中人、策略集、赢得函数称为对策的三要素。
十四.灰色预测法
1.参考博文:https://blog.csdn.net/shujuelin/article/details/82467667
2.优点:所需建模信息少、运算方便、建模精度高,适应于小样本预测问题。
3.matlab代码:
%%构建GM模型计算出a和b
%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
u = [a b]';
%原始数列X0
X0 = input('请输入数据');
n = length(X0);
%对原始数列X做累加得到数列X1
X1 = cumsum(X0);
%对数列X1做等权邻值生成Z1
for i = 2: n
Z1(i) = (X1(i) + X1(i - 1)) / 2;
end
Z1(1) = []; %去除掉第一个元素
%构造数据矩阵
B = [-Z1; ones(1, n - 1)]';
Y = [X0]';
Y(1, :) = []; %去除掉第一个元素
%利用u = inv(B'*B)*B'*Y来求解
u = inv(B'*B) * B' * Y;
a = u(1, :);
b = u(2, :);
%%预测后续数据
%p是预测后续的数据量,根据情况可更改
p = 3;
%构建预测数列F
F = []; F(1) = X0(1);
for i = 2: (n + p)
F(i) = (X0(1) - b/a) * exp(-a*(i-1)) + b/a;
end
%对数列F累减还原,得到预测出的数据
G = []; G(1) = X0(1);
for i = 2: (n + p)
G(i) = F(i) - F(i-1);
end
disp('预测到的数据为: ');
G
%%模型检验
H = G(1: n);
%计算残差序列
E = X0 - H;
%法一:相对残差Q检验
%计算相对误差序列
epsilon = abs(E ./ X0);
%计算相对误差Q
disp('相对残差Q检验: ');
Q = mean(epsilon)
%法二:方差比C检验
disp('方差比C检验: ');
C = std(E, 1) / std(X0, 1)
%小误差概率P检验
S1 = std(X0, 1);
tmp = find(abs(E - mean(E)) < 0.6745 * S1);
disp('小误差概率P检验:');
P = length(tmp) / n
%%绘制曲线图(根据不同的题目以下的代码会有所不同,故不贴出来,大家自己动手写吧)
十五.模拟退火算法
1.参考博文:https://blog.csdn.net/weixin_40562999/article/details/80853354
2.优点:模拟退火算法是一个解决最优化问题的算法。
3.代码:
matlab实现(参考博文:https://www.cnblogs.com/jacksin/p/9173484.html):
clc,clear %清空环境中的变量
tic
iter = 1; % 迭代次数初值
a=0.99; %温度衰减系数
t0=120; %初始温度
tf=1; %最后温度
t=t0;
Markov=10000; %Markov链长度
load data1.txt %读入城市的坐标
city=data1;
n = size(city,1); %城市距离初始化
D = zeros(n,n);
for i = 1:n
for j = 1:n
D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2));
end
end
route=1:n;
route_new=route;
best_length=Inf;
Length=Inf;
best_route=route;
%%
while t>=tf
for j=1:Markov
%进行扰动,长生新的序列route_new;
if (rand<0.7)
%交换两个数的顺序
ind1=0;ind2=0;
while(ind1==ind2&&ind1>=ind2)
ind1=ceil(rand*n);
ind2=ceil(rand*n);
end
temp=route_new(ind1);
route_new(ind1)=route_new(ind2);
route_new(ind2)=temp;
else
ind=zeros(3,1);
L_ind=length(unique(ind));
while (L_ind<3)
ind=ceil([rand*n rand*n rand*n]);
L_ind=length(unique(ind));
end
ind0=sort(ind);
a1=ind0(1);b1=ind0(2);c1=ind0(3);
route0=route_new;
route0(a1:a1+c1-b1-1)=route_new(b1+1:c1);
route0(a1+c1-b1:c1)=route_new(a1:b1);
route_new=route0;
end
%计算路径的距离,Length_new
length_new = 0;
Route=[route_new route_new(1)];
for j = 1:n
length_new = length_new+ D(Route(j),Route(j + 1));
end
if length_new
十六.黄金分割法
1.适用范围:适用于任何单峰值函数?(?)求极小点的问题,甚至对函数可以不要求连续。
2.算法步骤:
步骤1 确定?(?)的初始搜索区间[?, ?]。
步骤2 计算?2 = ? + ?(? − ?),?2 = ?(?2)。
步骤3 计算?1 = ? + ?(? − ?),?1 = ?(?1),。
步骤4 若?2-?1≤ ?,停机;否则,转步骤5。
步骤5 若?(?1) ≤ ?(?2),则? = ?2, ?2 = ?1, ?(?2) = ?(?1), ?1 = ? + ?(? − ?), ?1 = ?(?1);
否则,? = ?1, ?1 = ?2, ?(?1) = ?(?2), ?2 = ? + ?(? − ?), ?2 = ?(?2).然后转步骤4。
3.代码:
%% 黄金分割法
% qcy
% 2016年12月22日23:43:40
clear;
close all;
clc
%%
fun = @(x) x.^2 - 2 * x - 3; % 匿名函数
x = -2:0.001:5;
f = x.^2 - 2*x - 3;
figure(1);
plot(x,f);
hold on;grid on;
title('f(x) = x^2 - 2x - 3');
SEARCH_MAX = 1e4;
X_LEN_EPS = 1e-4;
count = 0;
x_low = -2;
x_high = 5;
range = x_high - x_low;
x_low_try = x_low + (1-0.618) * range; % 右试探点
x_high_try = x_low + 0.618 * range; % 左试探点
while count X_LEN_EPS)
y_low_try = fun(x_low_try);
y_high_try = fun(x_high_try);
if y_low_try < y_high_try
x_high = x_high_try; % 更新右端点,左端点不动
range = x_high - x_low; % 更新x的搜索范围
x_low_try = x_low + (1-0.618) * range; % 更新试探点
x_high_try = x_low + 0.618 * range; % 更新试探点
else
x_low = x_low_try; % 更新右端点,左端点不动
range = x_high - x_low; % 更新x的搜索范围
x_low_try = x_low + (1-0.618) * range; % 更新试探点
x_high_try = x_low + 0.618 * range; % 更新试探点
end
plot( (x_high + x_low)/2 , fun((x_high + x_low)/2) ,'r.','markersize',7) %标记当前的位置
drawnow;
pause(0.2);
count = count + 1;
end
x_min = (x_high + x_low)/2 ;
y_min = fun(x_min);
plot(x_min,y_min,'mp','markersize',7) %标记当前的位置
4.参考博文:https://blog.csdn.net/qq_39543472/article/details/86490327
https://blog.csdn.net/qcyfred/article/details/53823408
十七.神经网络
1.这个好难,先贴上参考博文:https://blog.csdn.net/sunyueqinghit/article/details/81703931
十八.逐步回归法
1.逐步回归是线性回归的一种。其基本思想是将变量一个一个引入,引入的条件是其偏回归平方和经验是显著的。同时,每引入一个新变量后,对已入选回归模型的老变量逐个进行检验,将经检验认为不显著的变量删除,以保证所得自变量子集中每一个变量都是显著的。此过程经过若干步直到不能再引入新变量为止。这时回归模型中所有变量对因变量都是显著的。
2.spss实现:参考博文https://wenku.baidu.com/view/0cd1a735a32d7375a41780f1.html
matlab实现:https://blog.csdn.net/qq_32095939/article/details/76375684
总结类的博文:
1.https://blog.csdn.net/qq_36666756/article/details/82117980
2.https://gitchat.csdn.net/activity/5a56fa45da55c14ac48a7c11
3.https://blog.csdn.net/yillc/article/details/6740997
4.b站数学建模视频:https://www.bilibili.com/video/av29662479