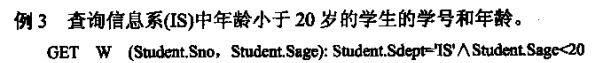对于元组关系演算ALPHA,始终有点不得要领,对于较为复杂的逻辑表达,虽然可以勉强看懂但是无法自己构造出来,特别是涉及到全称量词、存在量词和蕴含关系式的时候。
如果冷静下来仔细分析,其实从根本上来说,一直没有通过自然语言的逻辑结构来理解和表达想要完成的运算式,然而《数据库系统概论》这本书也是有些填鸭式教育,仅仅告诉你是什么却不解释为什么,所以我记录一下自己的一些方法论,来帮助学习和理解。
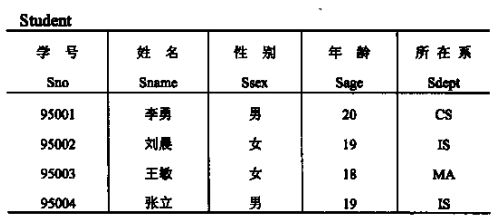
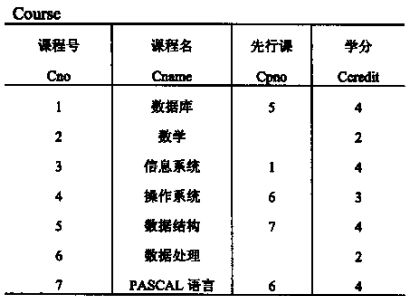
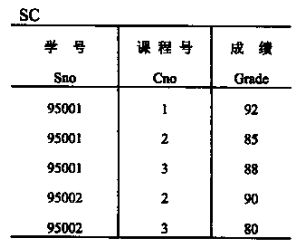
在谈问题之前,先把文章中需要用到的三张表放上来:
注意,本文只关注ALPHA语句中的检索条件部分,不关心其他部分。
首先谈及第一个问题:什么时候该使用量词?以下举出两个例子作对比,一个没有使用量词,另外一个使用了量词:
通过这个对比可以回答第一个问题,原则是:当所需要的查询结果只涉及某些表,但是查询过程需要用到这些表以外的其他的表的时候,需要使用量词;当所需要的查询结果涉及一些表,同时在查询过程中不需要涉及更多其他的表的时候,不需要使用量词。例3中,需要查询的是学生的学号和年龄,只涉及Student表,同时在查询的过程中不需要使用其他表,故不需要使用量词;例8中,需要查询的是学生的名字,然而要得到这个名字必须借助SC表的查询结果,所以这里我们要对SC表使用量词。
再来谈第二个问题:什么时候该用全称量词?什么时候该用存在量词?还是先上两个例子来对比说明:
这两个例子并不困难,但是可以作为我们进入更复杂表达式之前的一个训练,我的方法是通过严谨的自然逻辑语言来表达要求,然后将其转化为ALPHA,对于例8中的检索要求“查询选修2号课程的学生名字”,我们这样来表达:
1,对于当前时刻取到的一个Student元组,转入2进行判断。
2,当前时刻的Student元祖必须满足如下判断才是我们所需要的:在X表(X表就是SC对应的元组变量,因为ALPHA规定要使用量词必须使用元组变量,也就是说X就是SC表的一个别名)中是否存在一个元组,该元组的Sno等于该Student元组的Sno(X.Sno=Student.Sno?),且该元组的Cno=2(X.Cno='2'?)。如果当前Student元组满足以上条件,则把该Student元祖丢入结果集合,转3;如果不符合,直接转3
3,在Student表中依次取到下一条元组,若下一条元组存在,转1;若不存在(即当前元组是最后一条元组),直接结束,返回结果集合。
在针对于例12中的要求来写自然逻辑语言:
1,对于当前时刻取到的Student元组,转入2来判断。
2,当前Student元组必须满足如下条件才是我们所需要的:任取一个SCX元组,要么该SCX元组的Sno都不等于当前学生元组的Sno(因为选课并非强制,所以有些同学并没有选修任何课程,他当然也属于“不选1号课程的学生”这个范畴);要么该SCX元组的Sno等于当前Student元组的Sno但是该SCX元祖的Cno不等于1。如果当前Student元组符合了以上条件,则丢入结果集合,转3,;若不符合,直接转3。
3,在Student表中依次取到下一条元组,若下一条元组存在,转1;若不存在(即当前元组是最后一条元组),直接结束,返回结果集合。
针对于以上两个例子,在我加粗的地方是关键点,如果你的自然逻辑语言想要表达“存在一个”那么就应当使用存在量词;如果你想要表达“任选一个”(这时等同于“对所有的”),那么就应当使用全称量词。另外如果你的判断关系之间所使用的的连接词是且,这意味着判断关系之间要使用交集符合;如果判断关系之间的连接词词是要么,那就用并集符号。
以上例子都属于需求比较简单的一类,接下来看一个较为复杂的例子:
那么还是三段论:
1,对于当前时刻取到的一条Student元组,转入2来判断。
2,当前Student元组必须满足如下条件才是我们所需要的:任取一个CX元组,都存在一个SCX元组,该SCX元组的Cno等于该CX元组的Cno,且该SCX元组的Sno等于当前Student元组的Sno。若满足,则将当前Student丢入结果集,转3;若不满足,直接转3。
3,在Student表中依次取到下一条元组,若下一条元组存在,转1;若不存在(即当前元组是最后一条元组),直接结束,返回结果集合。
再来谈第三个问题:蕴含怎么使用?这个问题可以说是非常困难了,我先引用一个蕴含式的文字解释:
设p、q为两个命题。复合命题"如果p,则q"称为p与q的蕴含式,记作p→q。并称p为蕴含式的前件,q为后件。并规定p→q为假当且仅当p为真q为假。
这里要注意的是,蕴含式的返回值是一个布尔值,要么为TRUE要么为FALSE。举一个例子来帮助理解蕴含式:
p=我有钱
q=我买房
根据这个真值表,我们可以知道,当且仅当“如果我有钱,那么我不买房”的时候,这个蕴含式才会返回一个FALSE值,其他的诸如“如果我没钱,那么我买房”、“如果我没钱,那么我不买房”、“如果我有钱,那么我买房”都会返回TRUE值。
那么这个蕴含式如何在关系代数中运用呢?看一个例子:
如果你去专研这个例题给出的ALPHA表达式,那不难预见你会很难受,而且就算你看明白了你会陷入另一个矛盾,虽然能够理解这个表达式想要表达的意思但是却无法想出如何构造出这样一个逻辑复杂的式子,那么我们尝试用三段论来表达一下:
1,对于当前取到的Student元组,转入2进行判断。
2,当前取到的Student元组要满足如下判断:任取一个CX元组,如果存在一个SCX元组,SCX.Sno=95002且SCX.Cno=CX.Cno,但是不存在一个SCY元组,SCY.Sno=Student.Sno且CX.Cno=SCY.Cno,这说明该Student必然不是我们所需要的,直接进入3;否则必然满足要求,将该Student元组丢入结果集,进入3。
3,在Student表中依次取到下一条元组,若下一条元组存在,转1;若不存在(即当前元组是最后一条元组),直接结束,返回结果集合。
这里其实还是有点难以理解,但是相比于那个直接的ALPHA式子,我们至少能够看到一个更加符合我们思考方式的逻辑线,目前我还没有想好如何用更清晰地方式阐述阐述何种逻辑字眼的时候需要使用蕴含,容我再思考一下。