dynamic-programming-python-leetcode(动态规划)
1、Min Cost Climbing Stairs
On a staircase, the i-th step has some non-negative cost cost[i] assigned (0 indexed).
Once you pay the cost, you can either climb one or two steps. You need to find minimum cost to reach the top of the floor, and you can either start from the step with index 0, or the step with index 1.
Example 1:
Input: cost = [10, 15, 20] Output: 15 Explanation: Cheapest is start on cost[1], pay that cost and go to the top.
Example 2:
Input: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] Output: 6 Explanation: Cheapest is start on cost[0], and only step on 1s, skipping cost[3].
Note:
costwill have a length in the range[2, 1000].- Every
cost[i]will be an integer in the range[0, 999].
解析:
题目的意思是:有n级台阶,每次可以选择向上跳1至2级,每一级台阶会有一定的花费,找到一种上台阶方法,使得上台阶的总花费为sum(cost[i])最小,i表示的是每一次所在的台阶;解题思路:动态规划:dp[x] = min(dp[x - 1], dp[x - 2]) + cost[x]
class Solution(object):
def minCostClimbingStairs(self, cost):
"""
:type cost: List[int]
:rtype: int
"""
# df存储的是到达某个台阶的花费
size = len(cost)
dp = [cost[0], cost[1]] # 可以从第一个位置开始,也可以从第二个位置开始
for x in range(2, size): # 遍历每一个台阶
dp.append(min(dp[x - 1], dp[x - 2]) + cost[x]) # 最小的花费等于当前台阶的cost加上到达当前台阶的最小花费
return min(dp[-1], dp[-2])
2、Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step解析:一共n层楼梯,每一次能爬一层或者两层,有多少种方式。明显是动态规划问题,可以用递归或者循环,递归自顶向下,循环自底向上,由于递归会产生重复的计算,因此这里选用循环方式,自底向上进行计算,数组a里面存储的是方式的数量,比如0层和1层的时候,就只有一种上楼梯的方式,当n大于1时,后面的数量是基于前面的层数进行计算的,详见代码:
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
a = [1,1]
for i in range(2, n + 1):
a.append(a[i - 1] + a[i - 2])
return a[n]
3、Best Time to Buy and Sell Stock
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Example 1:
Input: [7, 1, 5, 3, 6, 4] Output: 5 max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)
Example 2:
Input: [7, 6, 4, 3, 1] Output: 0
In this case, no transaction is done, i.e. max profit = 0.
解析:股票只能一次买入,一次卖出,计算整个股价历史中,能够获得的最大收益是多少
4、Maximum Subarray
Find the contiguous subarray within an array (containing at least one number) which has the largest sum.
For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6
5、Degree of an Array
Given a non-empty array of non-negative integers nums, the degree of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of nums, that has the same degree as nums.
Example 1:
Input: [1, 2, 2, 3, 1] Output: 2 Explanation: The input array has a degree of 2 because both elements 1 and 2 appear twice. Of the subarrays that have the same degree: [1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2] The shortest length is 2. So return 2.
Example 2:
Input: [1,2,2,3,1,4,2] Output: 6
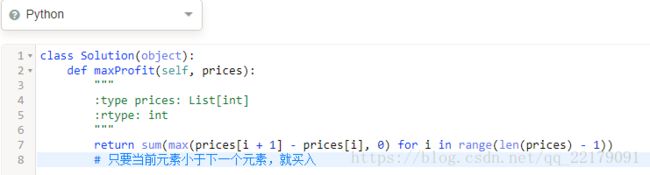
6、Best Time to Buy and Sell Stock II
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
7、House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
Credits:
Special thanks to @ifanchu for adding this problem and creating all test cases. Also thanks to @ts for adding additional test cases.
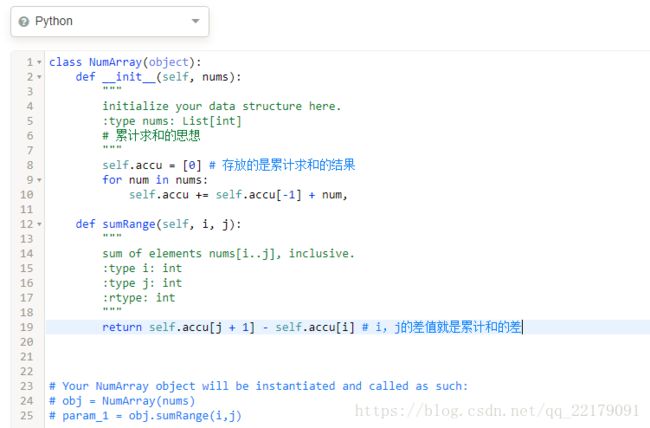
8、Range Sum Query - Immutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
Example:
Given nums = [-2, 0, 3, -5, 2, -1] sumRange(0, 2) -> 1 sumRange(2, 5) -> -1 sumRange(0, 5) -> -3
Note:
- You may assume that the array does not change.
- There are many calls to sumRange function.