Matlab一元非线性回归分析
Matlab一元非线性回归分析的分析步骤与一元线性回归分析的步骤类似:
大体分为以下几步:
(1)绘制x,y的散点图,分析散点图的走势;
(2)根据散点图的走势,确定回归方程的具体形式,特别是参数个数的设定和设定初始值;
(3)调用NonLinearModel的fit方法进行模型拟合;
(4)模型改进,去除异常值的操作;
(5)进行残差分析,验证模型。
下面以某商品的数量与定价为例,进行实例展示;
(1)绘制x,y的散点图,分析散点图的走势;
[data,y0]=xlsread('C:\Users\箫韵\Desktop\Matlab数理与统计分析\exdata\test1',3);
x=data(:,2);%提取列数据自变量数据
y=data(:,3);%提取列数据因变量数据
figure;
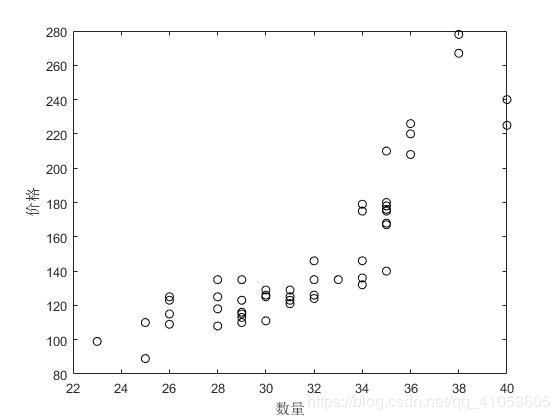
plot(x,y,'ko');%绘制散点图
xlabel('数量');
ylabel('价格');
图1 散点图
(2)根据散点图的走势,确定回归方程的具体形式,特别是参数个数的设定和设定初始值;
%建立一元非线性回归方程
% yi=f(xi;b1,b2)+ai
% ai~N(0,aa^2),i=1,2,..n
price=@(beta,x)beta(1)./(1-beta(2)*x);%根据散点图趋势建立方程f(x)=b1./(1-b2*x),方程形式并不唯一。
beta0=[120,0.008];%beta0为b1,b2的初始值。根据x的取值范围,x在22与40之间,y>0,故需b2<0.25。
%根据y值是84到280的不等分布,主要集中在110到130,故b1取值120较合适,根据方程,b2取0.008即可。
opt=statset;%创建结构体变量类
opt.Robust='on';%开启回归稳健性方法
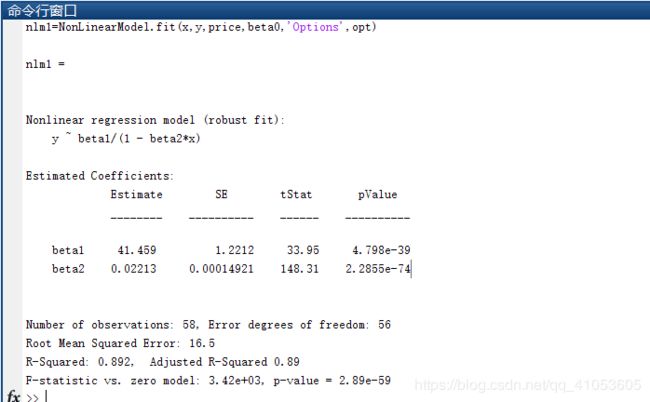
nlm1=NonLinearModel.fit(x,y,price,beta0,'Options',opt);
%y=41.459./(1-0.02213*x)
(3)调用NonLinearModel的fit方法进行模型拟合;
xnew=linspace(20,40,50)';%取50个x的值在20到40之间
ynew=nlm1.predict(xnew);%进行ynew预测
figure;
plot(x,y,'ko');
hold on;
plot(xnew,ynew,'linewidth',2.5);
xlabel('数量');
ylabel('价格');
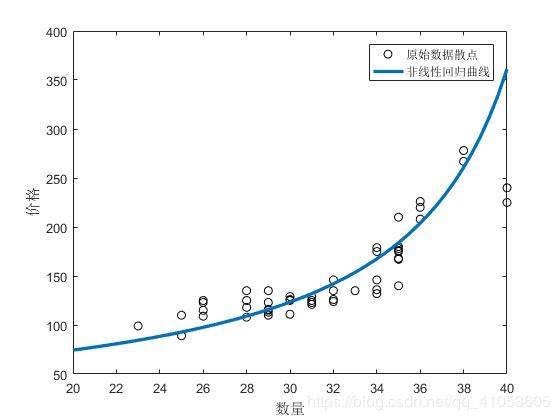
legend('原始数据散点','非线性回归曲线');
图2 模型拟合效果
(4)模型改进,去除异常值的操作;
异常值的诊断。NonlinearModel类对象的Residuals属性值中有标准化残差和学生化残差值。这里通过学生化残差查询异常值
Res2=nlm1.Residuals;
Res_Stu2=Res2.Studentized;
id2=find(abs(Res_Stu2)>2);
%properties(nlm1);%可以查询nlm1的属性
%去除异常值重新构建回归模型
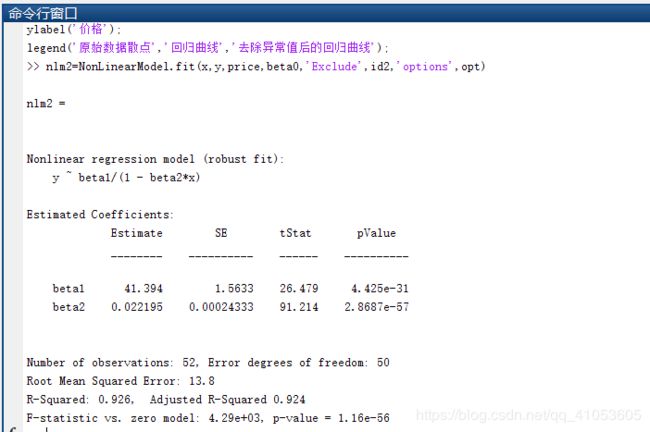
nlm2=NonLinearModel.fit(x,y,price,beta0,'Exclude',id2,'options',opt);
%y=41.394./(1-0.22195*x)
xnew=linspace(20,40,50)';
y1=nlm1.predict(xnew);
y2=nlm2.predict(xnew);
figure;
plot(x,y,'ko');
hold on;
plot(xnew,y1,'r--','linewidth',2);
plot(xnew,y2,'b.','linewidth',2);
xlabel('数量');
ylabel('价格');
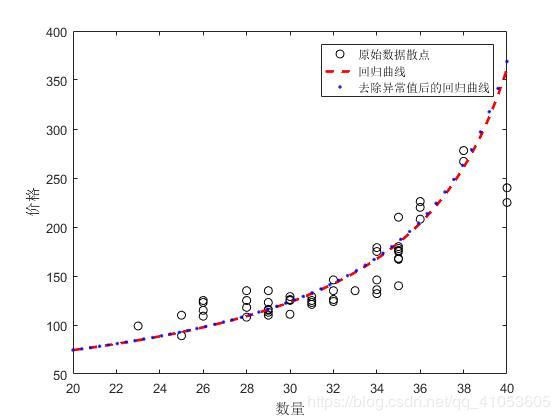
legend('原始数据散点','回归曲线','去除异常值后的回归曲线');
图3 去除异常值与未去除异常值的拟合对比
(5)进行残差分析,验证模型。
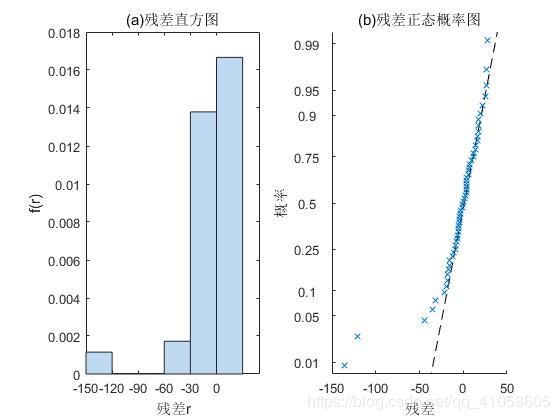
调用的是NonLinearModel类中的plotResiduals方法。残差分析有比较多的方法,这里以残差直方图和残差正态概率图为例。
%回归诊断
figure;
subplot(1,2,1);
nlm1.plotResiduals('histogram');
title('(a)残差直方图');
xlabel('残差r');
ylabel('f(r)');
subplot(1,2,2);
nlm1.plotResiduals('probability');
title('(b)残差正态概率图');
xlabel('残差');
ylabel('概率');
图4 残差直方图和残差正态概率图
| order | 数量 | 价格 |
| 1 | 25 | 89 |
| 2 | 28 | 108 |
| 3 | 26 | 115 |
| 4 | 23 | 99 |
| 5 | 26 | 109 |
| 6 | 32 | 124 |
| 7 | 35 | 210 |
| 8 | 30 | 126 |
| 9 | 34 | 132 |
| 10 | 29 | 110 |
| 11 | 33 | 135 |
| 12 | 36 | 226 |
| 13 | 34 | 136 |
| 14 | 36 | 220 |
| 15 | 36 | 208 |
| 16 | 30 | 125 |
| 17 | 32 | 146 |
| 18 | 30 | 129 |
| 19 | 35 | 140 |
| 20 | 29 | 116 |
| 21 | 31 | 123 |
| 22 | 32 | 126 |
| 23 | 28 | 135 |
| 24 | 36 | 208 |
| 25 | 40 | 240 |
| 26 | 28 | 125 |
| 27 | 29 | 113 |
| 28 | 36 | 208 |
| 29 | 32 | 135 |
| 30 | 38 | 267 |
| 31 | 40 | 225 |
| 32 | 38 | 278 |
| 33 | 28 | 118 |
| 34 | 32 | 124 |
| 35 | 34 | 146 |
| 36 | 36 | 208 |
| 37 | 30 | 111 |
| 38 | 29 | 115 |
| 39 | 36 | 208 |
| 40 | 29 | 123 |
| 41 | 25 | 110 |
| 42 | 29 | 135 |
| 43 | 26 | 123 |
| 44 | 23 | 99 |
| 45 | 26 | 125 |
| 36 | 35 | 180 |
| 37 | 35 | 178 |
| 38 | 35 | 175 |
| 39 | 35 | 176 |
| 40 | 35 | 180 |
| 41 | 35 | 178 |
| 42 | 34 | 175 |
| 43 | 35 | 168 |
| 44 | 35 | 167 |
| 45 | 34 | 179 |
| 43 | 31 | 129 |
| 44 | 31 | 121 |
| 45 | 31 | 125 |