初步学习k-NN算法以及使用GridSearchCV进行调参

k最近邻算法 (k-NN)

  k最近邻 (k-Nearst Neighbor, k-NN) 算法是一种比较简单易懂的机器学习算法，1968年由Cover和Hart提出，常应用于字符识别、文本分类、图像识别等领域。该算法的思想是：一个样本与数据集中的k个样本最相似，如果这k个样本中的大多数属于某一个类别，则该样本也属于这个类别。
  在sklearn库中，k-NN包含在sklearn.neighbors中，有k最近邻分类KNeighborsClassifier和k最近邻回归KNeighborsRegressor。本文以k-NN分类器为例进行学习。
  sklearn库中的k-NN方法有很多超参数，常用的超参数如下：
  1. weights：用于分配权重。基本的最近邻回归使用统一的权重，即本地邻域内的每个邻点对查询点的分类贡献一致。在某些环境下，对邻点加权可能是有利的，使得附近点对于回归所作出的贡献多于远处点。默认为weights = 'uniform'，表示为所有点分配同等权重。weights = 'distance'表示分配的权重与查询点距离呈反比。此外，我们还可以自定义一个距离函数用来计算权重。
  2. n_neighbors：邻居个数。
  3. p：p参数只有在weights = 'distance'时才有。p是一个大于或等于1的值。p = 1表示曼哈顿距离 (Manhattan Distance)，p = 2表示欧式距离 (Euclidean Distance)，p = ∞表示它是各个坐标距离的最大值。
  下面介绍一下三种距离计算公式。设特征空间$\mathcal{X}$是$n$维实数向量空间$R_n$，$x_i,x_j\in \mathcal{X}$，$x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)}{)}^T$，$x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)}{)}^T$，$x_i,x_j$的$L_p$距离定义为$$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}}.$$上式中$p\ge 1$. 当$p=1$时，称为曼哈顿距离，此时$$L_1(x_i,x_j)=\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|.$$当$p=2$时，称为欧式距离，此时$$L_2(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2{)}^{\frac{1}{2}}.$$当$p=\infty$时，表示各个坐标距离的最大值，此时$$L_{\infty }(x_i,x_j)={\max }_l|x_i^{(l)}-x_j^{(l)}|.$$
  接下来简单说明一下k-NN的算法流程。输入训练数据集$$T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N),$$其中$x_i\in \mathcal{X}\subseteq R^n$为实例的特征向量，$y_i\in \mathcal{Y}=\{c_1,c_2,...,c_k\}$为实例的类别，$i=1,2,...,N$；实例特征向量$x$.
  1. 根据给点的距离度量，在训练集$T$中找出与$x$最近邻的$k$个点，涵盖着$k$个点的领域，记为$N_k(x)$.
  2. 在$N_k(x)$中根据分类决策规则（如多数表决），决定$x$的类别$y$：$$y=arg{\max }_{c_j}{\sum }_{x_i\in N_k(x)}I(y_i=c_j),i=1,2,...,N;$$在上式中，$I$为指示函数，即当$y_i=c_j$时，$I$为$1$，否则$I$为$0$.
  最后输出实例$x$所属的类$y$.
  k-NN的特殊情况是k=1的情形，称为最近邻算法。对于输入的实例点（特征向量）$x$，最近邻算法将训练数据集中与$x$最近邻点的类作为$x$的类。

GridSearchCV调参

  GridSearchCV包含在sklearn.model_selection中。它可以拆分为“GridSearch”和“CV”两个部分，即网格搜索和交叉验证。网格搜索用于选取模型的最优超参数。获取最优超参数的方式可以绘制验证曲线，但是验证曲线只能每次获取一个最优超参数。如果多个超参数有很多排列组合的话，就可以使用网格搜索寻求最优超参数的组合。网格搜索针对超参数组合列表中的每一个组合，实例化给定的模型，进行交叉验证，将平均得分最高的超参数组合作为最佳的选择，返回模型对象。

GridSearchCV(estimator, param_grid, scoring=None, fit_params=None, n_jobs=1, iid=True,
             refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score='raise',
             return_train_score=True)

  以下是GridSearchCV方法中常用的超参数。
  1. estimator：创建的算法对象。
  2. param_grid：值为字典或者列表，需要最优化的参数的取值。
  3. scoring：准确度评价标准，默认None,这时需要使用score函数；或者如scoring='roc_auc'，根据所选模型不同，评价准则不同。字符串（函数名）或是可调用对象，需要其函数签名，形如scorer(estimator, X, y)；如果是None，则使用estimator的误差估计函数。
  4. n_jobs：并行数，默认为1，n_jobs = -1表示跟CPU核数一致。
  5. cv：交叉验证参数，默认None，使用三折交叉验证。指定fold数量，默认为3，也可以是yield训练或测试数据的生成器。
  6. verbose：日志冗长度。verbose = 0表示不输出训练过程，verbose = 1表示偶尔输出，verbose > 1表示对每个子模型都输出。
  GridSearchCV还内置了一些属性。
  1. best_estimator_：效果最好的分类器。
  2. best_score_：成员提供优化过程期间观察到的最好的评分。
  3. best_params_：描述了已取得最佳结果的参数的组合。
  4. best_index_：对应于最佳候选参数设置的索引（cv_results_数组的索引）。

优化Titanic生存预测代码

  在上一篇博客中，我使用决策树和k-NN两种分类器对处理后的Titanic数据集进行了分类预测，其中k-NN分类器的training set score为0.82，test set score为0.72，还有一部分优化空间。下面用网格搜索和交叉验证进行调参。

# 使用GridSearchCV进行调参
from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
param_grid = [
    {
        'weights': ['uniform'],
        'n_neighbors': [i for i in range(1, 11)]
    },
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(1, 11)],
        'p': [i for i in range(1, 6)]
    }
]
grid_search = GridSearchCV(knn, param_grid, n_jobs=-1, verbose=2)

%%time
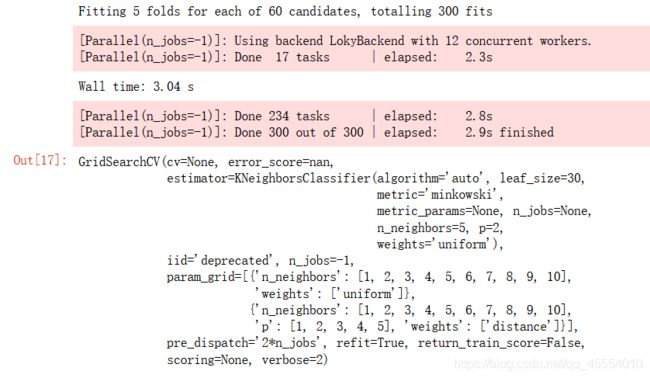
grid_search.fit(X_train, y_train)

  接下来查看一下GridSearchCV的属性。

# 最优超参数组合对应的分类器
grid_search.best_estimator_

# 最优超参数组合
grid_search.best_params_

# 最优超参数组合对应的准确率
grid_search.best_score_

  最后我们使用最优的分类器模型对测试集进行预测。

knn = grid_search.best_estimator_
y_predict = knn.predict(X_test)
print(y_predict)
print('Training set score: {:.2f}'.format(knn.score(X_train, y_train)))
print('Test set score: {:.2f}'.format(knn.score(X_test, y_test)))

  可以看出training set score有了明显的提升（从0.82提升到0.98），但是test set score的提升不是很多（从0.72提升到0.73）。