p-value&FPR以及q-value&FDR
首先我们来看 P-value的定义:在假设检验中,当原假设(H0)为真时,所得到的样本观察结果或更极端结果出现的概率。
如果P-value很小,说明原假设为真时,这个数据甚至更极端的数据出现的概率很小;而当P-value小于一个我们人为预先设定的值α(生物分析中一般取0.05)的时候,与其相信这个小概率事件的发生,我们认为更为合理的选择是拒绝原假设(H0)。
下面引用在网上看到的一个解释,十分简洁易懂。
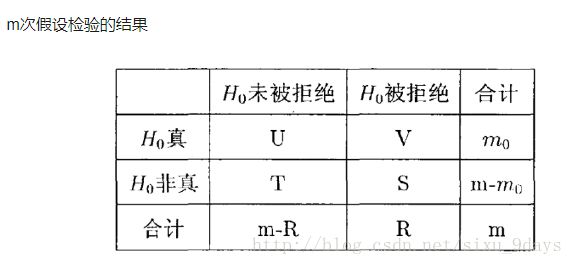
好了,理解了P-value的概念后,为了方便理解接下来的概念,用一张表格来表示假设检验的结果:
如果我们有m个基因,那么我们就要做m次假设检验。每一次的假设检验的零假设H0为:两个样本的这个基因没有显著性差异。其中有m0个零假设是正确的,即这个基因在两个样本中确实没有显著性差异;但有m1=m-m0个零假设是错误的,即两个样本的这个基因是有显著性差异。m次检验之后,被拒绝的零假设的个数记为R。
我们再回头思考刚才的问题:原假设(H0)为真时,当P-value小于α,拒绝了原假设(H0)。这同时出现了假阳性的情况:H0是无效假设(阴性),拒绝了H0就意味着认为是阳性结果;同样的,这也是假设检验中的第一类错误:否定真实假设的错误,亦称弃真错误。因此p-value本质是控制假阳性率(False positive rate,FPR)。
假设检验的目的是make decision. 传统上把小概率事件的概率定义为0.05或0.01, 但不总是这样. 主要根据研究目的. 在一次试验中(注意:是一次试验, 即single test),0.05 或0.01的cutoff足够严格了(想象一下, 一个口袋有100个球, 95个白的, 5个红的, 只让你摸一次, 你能摸到红的可能性是多大?). 我刚才强调的是single test, 在multiple test中, 通常不用p-value, 而采用更加严格的q-value. 与p-value 不同,q-value 控制的是FDR (false discovery rate)。
什么是FDR?给出定义:错误发现率,表示了在所有R次拒绝中错误发现的期望比例。错误发现率和假阳性率之间有着本质的差别。错误发现率将范围限定在总的拒绝次数中,即FDR = E(V/R);而假阳性率则针对所有变量数而言。需要在错误发现次数V和总的拒绝次数R之间寻找一种平衡,即在检验出尽可能多的候选变量的同时将错误发现率控制在一个可以接受的范围。
为什么在multiple test 中要采用q-value进行判断呢?
举个例子.假如有一种诊断艾滋病(AIDS)的试剂, 试验验证其准确性为99%(每100次诊断就有一次false positive). 对于一个被检测的人(singletest) 来说, 这种准确性够了. 但对于医院 (multiple test) 来说,这种准确性远远不够, 因为每诊断10000个个体, 就会有100个人被误诊为艾滋(AIDS).这显然是不能接受的。所以,对于多重检验,如果不进行任何控制,犯第一类错误的概率便会随着假设检验的个数迅速增加。为了合理控制,有必要引入一个更加严格的指标,也就是q-value。它就是校正后的p-value
在多重假设检验中,有许多方法来克服这个问题。比如对每个测试用例赋校正后的p-value,或者将 p-value 的阈值从0.05下降到一个更为合理的阈值。许多传统的技术例如Bonferronicorrection从某种意义上来说显得较为保守,他们主要是依靠减少假阳性的个数,同时也会减少 TDR (True Discovery Rate)。FDR方法则是一种更加新颖靠谱的方法。这个方法同样会对每个测试用例赋校正后的p-value,但是,它还控制了错误发现的个数。即在检验出尽可能多的候选变量的同时将错误发现率控制在一个可以接受的范围。
那么如何用FDR对P-value校正呢?Benjamini和Hochberg提出了以FDR作为多重检验的准则,但是其检验的方法采用的是Simes(1986)提出的算法。设总共有m个候选基因,每个基因对应的p值从小到大排列分别是p(1),p(2),... p(m),则若想控制fdr不能超过q,则只需找到最大的正整数i,使得p(i)<= (i*q)/m。然后,挑选对应p(1),p(2),...,p(i)的基因做为差异表达基因,这样就能从统计学上保证fdr不超过q(这个可以推导出来,比较容易,就不演示了)。