[论文笔记] Sigcomm 2018 Elastic Sketch: Adaptive and Fast Network-wide Measurements

先附上论文的GitHub链接
做实验的话真的得看这篇，有那么多可以实验的角度。

除了basic version的方式分离象流和鼠流，以及MM合并的一个bound
其他都没给出数学上的证明。（居然在技术报告里）

我简直有毒，在heavyguardian里面，除了算法，什么都写了。
再次强调不要犯懒，复习的时候真的只想看自己的博客，不想点开别人的了。一定要把一些事情的意义写上去。

基于sketch的网络测量方法介绍
别人的大四VS我的大四orz

introduction

网络测量对数据中心和骨干网的network operations, quality of service, capacity planning, network accounting and billing, congestion control, anomaly detection都是必不可少的。

由于基于sketch的解决方法比抽样方法准确率要高，因此它们被广泛采用。主要是寻求accuracy、speed、和内存的平衡。
最前沿的算法UnivMon还关注于generality，即用一个sketch来实现多种任务。
但是他们都没有将sketch设计的符合网络的变化，网络测量在网络遭遇问题的时候重要性尤为凸显，网络特性急剧变化会极大降低测量性能。

available bandwidth

在数据中心，管理员更关注网络全局状态（network-wide measurements），他们可以在网络中部署很多测量节点，周期性地向controller报告，发送这些测量信息和用户流量是共享数据平面带宽的。但是拥塞经常发生，It can happen frequently within a single second [19] and be as large as more than half of the network bandwidth [9].
Network measurements should not be a burden for the network.
A good solution is to actively compress the sketch with little accu- racy loss, thereby reducing bandwidth usage.
省略省略，总之就是测量很重要，拥塞时更加需要测量来发现问题解决问题，但是拥塞时又没有带宽留给测量，因此应该压缩sketch、
Besides passive compression during congestion, network operators need to proactively control the measurement tasks as well. For example, to keep service- level agreements (SLA) during maintenance or failures [28], operators tend to reduce measurements and leave the band- width for critical user traffic.

packet arrival rate

当网络被扫描或者受到DDoS攻击时，包会很小很多. The processing speed of existing sketches on software platforms is fixed in terms of packet rate. 因此包到达率突然增大的时候不work，不能记录一些重要的信息。因此要加速sketch的处理速度。
state-of-art solution：SketchVisor，使用fast path组件absorb excessive traffic at high packet rate.但是在最坏情况下要遍历整个数据结构，虽然更新复杂度是O(1)。要多次访问内存。本文算法只需要一次

flow size distribution

鼠流和象流应该分开，但是flow size distribution一直在变，导致分配多大的内存存储需要跟着变化。预测是不OK的，预测一小时内象流的数量可能很简单，但是ms级别或是s级就很难[39]，因此设计了动态分配合适内存给象流的方法。
Besides them, there are three other requirements in measurements: 1) generic, 2) fast, and 3) accurate
已有的generic的算法是UnivMon和FlowRadar，本文实验中发现UnivMon准确度不太好，FlowRadar消耗大量内存。

FlowRadar在Bloom Filter和Invertible Bloom Lookup table （可逆式布鲁姆查找表）里面记录了所有的流ID和大小。为了减少内存消耗，踢出network-wide decoding，但是内存消耗还是比sketch要高。
UnivMon的关键技术是universal streaming，准确度由它来保证。它是第一个generic的，性能还不错，但是不适应多变的网络。

our solution

Ostracism分离鼠流和象流
elastic：
generic：

• 保存每个包所有必要信息，丢弃鼠流的ID信息(耗内存且无用)
• 提出软件和硬件版本的改进，为P4量身设计了一个版本
  Owing to the separation and discarding of unnecessary information, our sketch is accurate and fast: experimental results show that our sketch achieves 44.6~45.2 times faster speed and 2.0 ~273.7 smaller error rate than the state-of-the-art UnivMon

key contribution

简而言之

1. 适应于多变的网络
2. 核心技术是分离大象流和老鼠流，以及sketch压缩
3. 在多个平台上又快又好的实现。

Basic version中的OStracism

given a high-speed network stream, how to use only one bucket to select the largest flow?

看到 ostracism 的时候，感觉和
数据流基本问题–确定频繁元素（一） 中提到的，我觉得思想是一致的，然后引入一个$\lambda$
λ的作用是什么呢？
flag的作用是判断bucket里面是否evicted过
如果两个大象流碰撞了，或者三个，那么其中一个就有可能被evicted入light part，那么信息就没有得到很好的保存
如果我就用编程之美中提到的方法，那么cold item的信息是就全没有，而且hot item的信息会被预估的小？（不考虑碰撞的话）lambda越大，存的vote+应该就越准
它这相当于$\lambda =1$就驱逐

accuracy analysis

${\hat{f}}_i⩽f_i+ϵ{\Vert f_l\Vert }_1^4<f_i+ϵ\Vert f{\Vert }_1$

where fL denotes the size vector of the sub-stream recorded by light part
$\Vert \mathbf{x}{\Vert }_1$ is the first moment of vector $\mathbf{x},$ i.e., $\Vert \mathbf{x}{\Vert }_1=\sum x_i$

准确度最差的情况：象流发生了碰撞，如果象流碰撞，那么一个象流会被放入light part，使得鼠流被大幅度over-estimated
elephant collision rate $P_{hc}$：定义为发生碰撞的桶数除以总桶数。
$P_{hc}=1-\left(\frac{H}{w}+1\right)e^{-\frac{H}{w}}$
H是象流数目，w是桶数
解决象流碰撞问题的办法（其实就是减少哈希碰撞）：by using multi- ple sub-tables (see Section 4.2); 2) by using multiple key-value pairs in one bucket

adaptive to bandwidth

发的sketch太大会影响时延和用户流量

Compression of Sketches

两步走 先group，然后把同一组中的merge
合并的时候有两个选择，取sum，那么和直接存的accuracy是一样的，本文使用的是maximum，使用了原先sketch更多的信息，也有更高的效率

compress light

分组相当于什么叭，数论里面的完全什么什么集 {0} {1} … {r-1}
mod 3为1的放入一组，选择组中最大的，然后你mod 3为1就能找回这个数据。按照原图去找，要找到之前的位置是3k+1，在3k+1里面选择最大的去保留
merge就是在同组里面选最大的。生成B之后还是d个hash function，映射之后找最小的。会有over-estimate error

这个所谓的同样的accuracy是指什么？
他这里的同样的accuracy，指的是用一个大S1,1/2小S2的accuracy 和只用一个大S1，然后把它/2 是一样的
这是非常直观的，你想hash入更小的sketch，可不就是直接相加吗？
难点在于如何让后者有更高的accuracy。选择采用MAX 而不是SUM，因为MAX能留住更多的信息。（原话是这么翻译过来的）
MAX的误差界限：

$\mathrm{Pr}\left\{{\hat{n}}_j⩾n_j+ϵN\right\}⩽{\left\{1-\left(1-\frac{1}{ϵzw}\right){\left[1-\frac{N}{zw\left(n_j+ϵN\right)}\right]}^{z-1}\right\}}^d$
这居然也能数学证明，数学厉害死了。

• MC比SC(sum compression)的误差界更紧一点
• 证明使用MC，只有over-estimation错误，没有under-estimation错误
• 使用SIMD（single Instruction and multiple data）加速5~8倍
• 没有解压缩的必要
• 压缩不需要额外的数据结构
  以上在technical report都有证明

Merging of Sketches 多个不同的sketch进行合并

在合并的过程中选择max，可以避免under-estimation error

adaptive to packet error

现有的sketch方案的processing speed是常数（应该不能这么翻译emm），但是处理一个包需要不小于10 memory access。设计目标是在packet rate low的时候两次存取，high的时候一次存取。但是难以维持高准确率。
卖点：只需要一次内存存取。
概括：插入的时候只对heavy part进行操作。注意并不是丢弃light part，因为查询的时候还要用到。
packet rate变得很high，插入时：如果$f$被$f^{{}^{\prime }}$代替，$f^{{}^{\prime }}$的大小被置为$f$的大小。这样，每次插入只需要访问一次bucket。在插入的时候是不访问light part的。
当速度慢下来，就用之前的算法。
我想知道accuracy降低了多少
This means that only information recorded by the light part when high packet rate occurs is lost. This strategy does not affect much the query accuracy in most cases, since the packet rate is usually low.

adaptive to flow size distribution

hard to predict[39]
概括：copy operation
flow size distribution的一个关键指标是大象流的个数，它经常变，因此我们需要动态调整Heavy part的大小。如果bucket中记录的流大小超过T2的流数超过T1，就启动copy operation：将heavy part直接复制一份，copied和之前的合起来。那么之前的有一半的需要移动。怎么理解呢？比如说我原先是h%4， 我现在size由4变成8，现在是h%8，但是h%8结果中会包含h%4的部分，因此这部分bucket不需要移动，但是值为5-7的部分需要后移。算法执行a lazy elimination，插入的时候如果出现碰撞，才把原先的移出，新的插进去。
比如$f^{{}^{\prime }}$应该被插入bucket A，检查bucket A中其他的flow，这些flow应该有一半是不属于这个bucket了，然后把这些给removed。对这部分代码有疑问。每次插入都去检查，岂不是很浪费时间？
还有当我来一个新的$f^{{}^{\prime }}$的是时候，我怎么知道$f$是应该直接被remove还是按照正常流程增加它的negative vote，然后把它移入light part。我还是要检查一下$f$，是新插入的还是之前
而且从之前的heavyGuardian中来看，并没有存hash值。
Overhead：由于heavy part一般很小（150KB），复制花的时间可以忽略不计

把多键值对和单键值对的情况混在一起讲很难理解啊(#`O′)

不仅可以enlarge heavy part，也可以压缩heavy part，合并的buckets。比较两个buckets里面记录的flow的频次，保留大的那个，将小的驱逐进light part来释放内存。
这里又有一个问题了，如果是using multiple key-value pairs in one bucket的防碰撞机制，如何压缩？

不同的平台用不同的防碰撞方法

看了视频里三个提问
1、如何得到flow ID
2、如何合并compressed和non compressed sketch
3、如何做cardinality estimation 线性那个啥
不同种类的sketch的影响，CU的accuracy会更高，为什么没用呢？因为硬件不支持某个操作
同时CU好像不支持删除操作sketch调研

optimization

light part部分优化

使用的hash函数个数减少为1，因为accuracy已经够高了，更关注实现的可行性和速度

硬件版本优化——multiple sub-tables

每个子表的操作都和basic version相同，但是用不同的hash函数。大象流的碰撞概率随着子表的个数呈指数递减。
每个子表操作相同，因此适合各种硬件平台。

插入和之前没啥区别，查找的时候要把所有表加起来。注意他是按顺序的先第一张表，再第二张表，这意味着可能第二张表存了f4,第一张表之后f4来的时候刚好evict走一个别的，因此要把两个heavy part都查询了然后加起来。

根据实验，使用4张表能够在准确度和可实现性上达到很好的平衡

软件版本优化——multiple key-value pairs

一个bucket里存多个flow的数据，bucket size会比a machine word大，存取会成为瓶颈。幸运的是，可以使用SIMD在CPU平台上加速该过程，因此这种优化方式适合软件平台。
所有的流共享negative vote，比值超过$\lambda$驱逐的时候驱逐size最小的flow，然后把共享的negative vote置为0。

application

generic：
知道IDs和flow size，可以处理以下任务。
据观察，鼠流的ID不需要

flow size estimation

本文中用包数作为flow size，也可以策略bytes数（假设最小包64byte，如果一个包是120bytes，向上取整我们就认为是2个包）
heavy part里面flag=false的流的大小都是准确的。more than 56.6% flows in the heavy part have no error when using 600KB memory for 2.5M packets

heavy hitter detection

查询heavy part，如果flow size大于一个固定的阈值，就报告为heavy hitter。只有小部分与light part进行交换过的有误差。

heavy change detection

没啥好说的 和hitter差不多

flow size distribution，entropy，and cardinality

这些任务不仅仅关注大象流，还关注鼠流。在heavy part里的信息直接获取，在light part里的部分，根据counter distribution获得需要的信息。在每个时间窗的末尾，收集counter distribution信息，即值为i的counter有多少个。然后把heavy part和压缩后的light part以及记录counter distribution的array一起发给collector。

1. flow size distribution ： MRAC算法去估计light part部分的distribution，然后加上heavy part部分的估计
   MRAC
   
   
   还有web traffic 和 DNS traffic 的
   
   不想看MRAC的论文，下次下次。

HeavyGuardian是以概率驱逐，这个是给一个阈值，这个估计流的分布为什么不能按照heavyguardian的方式呢？这两种估计方式的优劣何在？

2. entropy
   是基于flow size distribution的，没啥好说的
3. cardinality：先是在heavy part统计，然后再light part用线性计数法计算。让我来瞅瞅这个线性计数法是什么？
   关于cardinality estimation，这里突然插入？如果多的话我就放另一个博客~ 另一个博客见，反正是数学的天下。

其他任务比如说DDoS，SuperSpreader会在以后讨论。

implementation

we briefly describe the implementation of hardware and software versions of the Elastic sketch on P4, FPGA, GPU platforms, and CPU, multi-core CPU, OVS platforms, respectively.

P4 implementation

不懂硬件，不懂P4 orz
在基础的switch上构建了Elastic sketch的P4原型。在硬件版本里寄存器实现了heavy part和light part，而不是match-action表，因为需要直接从数据平面更新条目。We leverage the Stateful Algorithm and Logi- cal Unit (Stateful ALU) in each stage to lookup and update the entries in register array. 但是Stateful ALU资源有限，每一个Stateful ALU只能更新一对32bit的寄存器，但是硬件版本的Elastic需要插入时存取4个fields。为了解决这个问题，将Elastic sketch修改了一下以适应P4交换机，精度损失了一点。
在hard-ware版本的基础上做了如下变动：

• We only store three fields in two physical stages：vote ${}^{all},{\text{ and (key, vote }}^{+}),$ where vote ${}^{all}$指的是正投票和负投票的和。
• 当$\frac{vot{e}^{all}}{vot{e}^{+}}⩾{\lambda }^{\prime }$时，采取驱逐策略 ${\lambda }^{\prime }=32$,原因在技术报告section B里面。
• 
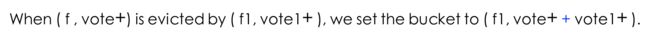
• As mentioned in Section 4.2, we recommend using 4 subtables in the hardware version. In this way, we only need 4*2=8 stages for the heavy part, and 1 stage for the light part, and thus in total 9 stages. ？？stage指的是什么

四个版本的elastic sketch性能对比

FPGA implementation

We implement the Elastic sketch on a Stratix V family of Altera FPGA (model 5SEEBF45I2). The capacity of the on-chip RAMs (Block RAM) is 54,067,200 bits. The resource usage information is as follows: 1) We use 1,978,368 bits of Block RAM, 4% of the total on-chip RAM. 2) We use 36/840 pins, 4% of the total 840 pins. 3) We use 2939 logics, less than %1 of the 359,200 total available. The clock frequency of our implemented FPGA is 162.6 MHz, meaning processing speed of 162.6 Mpps.

GPU Implementation

We use the CUDA toolkit [64] to write programs on GPU to accelerate the insertion time of Elastic sketch. Two techniques, batch processing and multi- streaming, are applied to achieve the acceleration. We use an NVIDIA GPU (GeForce GTX 1080, the frequency is 1607 MHz. It has 8 GB GDDR5X memory and 2560 CUDA cores).

Software Version Implementations

CPU, multi-core CPU, and OVS

experimental results

Experimental Setup

Traces：四个一小时的公共流trace collected in Equinix-Chicago monitor from CAIDA，将这些traces划分成不同的时间间隔（1s, 5s, 10s, 30s, and 60s）。比方说一个小时的traces可以划分为720个5s的子trace，we plot 10th and 90th percentile error bars across these 720 sub-traces.我们用5s间隔的trace作为默认trace，which contains 1.1M to 2.8M packets with 60K to 110K flows (SrcIP)。由于空间限制，只展示source IP作为flow ID的结果。the results are qualitatively similar for other flow IDs (e.g., destination IP, 5-tuple).
metrics

• ARE: $\frac{1}{n}{\sum }_{i=1}^n\frac{|f_i-f_i|}{f_i}$ $f_i$是实际的流大小，$f_i$是估计的流大小，使用ARE来评判flow size (FS) estimation and heavy hitter detection。Note that the value of ARE for ?ow size estimation could be larger than anticipated, since the sizes of mouse flows are often over-estimated while they are in the denominator of the ARE formula, leading to large average value of relative error
• F1 score: $\frac{2\times PR\times RR}{PR+RR}$
  PR refers to the ratio of true instances reported
  RR refers to the ratio of reported true instances 这个英语绝了，上面强调reported，下面强调true instances
• WMRE（weighted mean relative error）：$\frac{{\sum }_{i=1}^z|n_i-n_i|}{{\sum }_{i=1}^z\left(\frac{n_i+n_i}{2}\right)}$ z是流的最大size，$n_i$是大小为i的流的真实个数， $n_i$是大小为i的流的预估个数。用这个指标来估计flow size distribution(FSD)的精度
• RE（relative error）$\frac{|\text{True-Estimated}|}{\text{True}}$ 用来衡量熵和基数估计的精度
• Throughput：每秒百万个包，衡量6个任务的处理速度。
  和别的算法对比的时候，用软件版本的，在heavy part存储7 flows和一个vote${}^{-}$,light part使用一个hash函数和8bit计数器，每个任务的默认内存大小是600K。heavy part只在测试adaptivity to traffic distribution的时候会动态扩展。

Accuracy

the ARE of Elastic is about 3.8, 2.5, and 7.5 times lower than the one of CM, CU, and Count.
We find that our compression algorithm significantly improves the accuracy of CM sketch, making it nearly approach the accuracy of Elastic.

observed worst cases

测量误差来源：

• 象流被踢到了light part
• 一些流在light part产生碰撞
  In our experiments, over different traces, we observe that at most 2 flows have under-estimation error, and the maximum absolute error is 254 (i.e., a flow with size 1 is mapped to an overflowed counter). In each trace, there are about 110,000 flows and the maximum flow size is about 17,000. It means Elastic has small relative errors even in the worst case.

heavy hitter detection

Observed Worst Cases: Here, we show the observed worst cases of Elastic in the flow size estimation, instead of the average errors shown in the above flgures. Notice that the estimation error of Elastic comes from two parts: 1) Some elephant flows are recorded in the light part due to the hash collisions in the heavy part, and this may incur overflows of counters in the light part. 2) Some flows collide at the same counter in the light part. In our experiments, over different traces, we observe that at most 2 flows have under-estimation error, and the maximum absolute error is 254 (i.e., a flow with size 1 is mapped to an overflowed counter). In each trace, there are about 110,000 flows and the maximum flow size is about 17,000. It means Elastic has small relative errors even in the worst case.

• 因为碰撞象流进入了light part，象流导致overflow
• light part发生碰撞over different traces, we observe that at most 2 flows have under-estimation error
  

memory and bandwidth usage

We measure the memory and bandwidth usage of different algorithms to achieve a fixed target accuracy, using different traces and different monitoring time intervals.
memory指的是给测量算法起初分配的内存大小
bandwidth指的是每个测量周期需要被传输的数据量
测量bandwidth时（16MBwith 500KB heavy part）
When measuring the bandwidth usage of Elastic, we set the original memory to 16MBwith 500KB heavy part, run the maximum compression algorithm (§3.2.1), and measure the memory usage after compression (as the bandwidth usage) to achieve the fixed target accuracy
对于其他测量算法，memory=bandwidth
通过改变Monitoring time intervals 和Traces来进行测量

elasticity

Adaptivity to Bandwidth

Adaptivity to Packet Rate

Adaptivity to Traffic Distribution

让我们来瞅瞅 heavy part是如何实现的

#ifndef _HEAVYPART_H_
#define _HEAVYPART_H_

#include "param.h"




template<int bucket_num>
class HeavyPart
{
public:
	alignas(64) Bucket buckets[bucket_num];

	HeavyPart()
	{
		clear();
	}
	~HeavyPart(){}

	void clear()
	{
		memset(buckets, 0, sizeof(Bucket) * bucket_num);
	}


/* insertion */
	int insert(uint8_t *key, uint8_t *swap_key, uint32_t &swap_val, uint32_t f = 1)
	{
		uint32_t fp;
		int pos = CalculateFP(key, fp);	 //CalculateBucketPos(fp) % bucket_num即(fp) * CONSTANT_NUMBER) >> 15% bucket_num


		const __m256i item = _mm256_set1_epi32((int)fp); //__m256i:256位紧缩整数(AVX) 这个是SIMD变量命名规范
		__m256i *keys_p = (__m256i *)(buckets[pos].key);
		int matched = 0;

		__m256i a_comp = _mm256_cmpeq_epi32(item, keys_p[0]);
		matched = _mm256_movemask_ps((__m256)a_comp);

		if (matched != 0)
		{
			//return 32 if input is zero;
			int matched_index = _tzcnt_u32((uint32_t)matched);
			buckets[pos].val[matched_index] += f;
			return 0;
		}


		const uint32_t mask_base = 0x7FFFFFFF;
		const __m256i *counters = (__m256i *)(buckets[pos].val);
		__m256 masks = (__m256)_mm256_set1_epi32(mask_base);
		__m256 results = (_mm256_and_ps(*(__m256*)counters, masks));
	    __m256 mask2 = (__m256)_mm256_set_epi32(mask_base, 0, 0, 0, 0, 0, 0, 0);
	    results = _mm256_or_ps(results, mask2);

	    __m128i low_part = _mm_castps_si128(_mm256_extractf128_ps(results, 0));
	    __m128i high_part = _mm_castps_si128(_mm256_extractf128_ps(results, 1));

	    __m128i x = _mm_min_epi32(low_part, high_part);
	    __m128i min1 = _mm_shuffle_epi32(x, _MM_SHUFFLE(0,0,3,2));
	    __m128i min2 = _mm_min_epi32(x,min1);
	    __m128i min3 = _mm_shuffle_epi32(min2, _MM_SHUFFLE(0,0,0,1));
	    __m128i min4 = _mm_min_epi32(min2,min3);
	    int min_counter_val = _mm_cvtsi128_si32(min4);

	    const __m256i ct_item = _mm256_set1_epi32(min_counter_val);
	    int ct_matched = 0;

	    __m256i ct_a_comp = _mm256_cmpeq_epi32(ct_item, (__m256i)results);
	    matched = _mm256_movemask_ps((__m256)ct_a_comp);
	    int min_counter = _tzcnt_u32((uint32_t)matched);


		if(min_counter_val == 0)		// empty counter
		{
			buckets[pos].key[min_counter] = fp;
			buckets[pos].val[min_counter] = f;
			return 0;
		}


		uint32_t guard_val = buckets[pos].val[MAX_VALID_COUNTER];
		guard_val = UPDATE_GUARD_VAL(guard_val);


		if(!JUDGE_IF_SWAP(GetCounterVal(min_counter_val), guard_val))
		{
			buckets[pos].val[MAX_VALID_COUNTER] = guard_val;
			return 2;
		}

	
		*((uint32_t*)swap_key) = buckets[pos].key[min_counter];
		swap_val = buckets[pos].val[min_counter];


		buckets[pos].val[MAX_VALID_COUNTER] = 0;


		buckets[pos].key[min_counter] = fp;
		buckets[pos].val[min_counter] = 0x80000001;

		return 1;
	}

	int quick_insert(uint8_t *key, uint32_t f = 1)
	{
		uint32_t fp;
		int pos = CalculateFP(key, fp);	

		const __m256i item = _mm256_set1_epi32((int)fp);
		__m256i *keys_p = (__m256i *)(buckets[pos].key);
		int matched = 0;

		__m256i a_comp = _mm256_cmpeq_epi32(item, keys_p[0]);
		matched = _mm256_movemask_ps((__m256)a_comp);

		if (matched != 0)
		{
			int matched_index = _tzcnt_u32((uint32_t)matched);
			buckets[pos].val[matched_index] += f;
			return 0;
		}


		const uint32_t mask_base = 0x7FFFFFFF;
		const __m256i *counters = (__m256i *)(buckets[pos].val);
		__m256 masks = (__m256)_mm256_set1_epi32(mask_base);
		__m256 results = (_mm256_and_ps(*(__m256*)counters, masks));
	    __m256 mask2 = (__m256)_mm256_set_epi32(mask_base, 0, 0, 0, 0, 0, 0, 0);
	    results = _mm256_or_ps(results, mask2);

	    __m128i low_part = _mm_castps_si128(_mm256_extractf128_ps(results, 0));
	    __m128i high_part = _mm_castps_si128(_mm256_extractf128_ps(results, 1));

	    __m128i x = _mm_min_epi32(low_part, high_part);
	    __m128i min1 = _mm_shuffle_epi32(x, _MM_SHUFFLE(0,0,3,2));
	    __m128i min2 = _mm_min_epi32(x,min1);
	    __m128i min3 = _mm_shuffle_epi32(min2, _MM_SHUFFLE(0,0,0,1));
	    __m128i min4 = _mm_min_epi32(min2,min3);
	    int min_counter_val = _mm_cvtsi128_si32(min4);

	    const __m256i ct_item = _mm256_set1_epi32(min_counter_val);
	    int ct_matched = 0;

	    __m256i ct_a_comp = _mm256_cmpeq_epi32(ct_item, (__m256i)results);
	    matched = _mm256_movemask_ps((__m256)ct_a_comp);
	    int min_counter = _tzcnt_u32((uint32_t)matched);


		if(min_counter_val == 0)		
		{
			buckets[pos].key[min_counter] = fp;
			buckets[pos].val[min_counter] = f;
			return 0;
		}


		uint32_t guard_val = buckets[pos].val[MAX_VALID_COUNTER];
		guard_val = UPDATE_GUARD_VAL(guard_val);

		if(!JUDGE_IF_SWAP(min_counter_val, guard_val))
		{
			buckets[pos].val[MAX_VALID_COUNTER] = guard_val;
			return 2;
		}


		buckets[pos].val[MAX_VALID_COUNTER] = 0;

		buckets[pos].key[min_counter] = fp;
		return 1;
	}

/* query */
	uint32_t query(uint8_t *key)
	{
		uint32_t fp;
		int pos = CalculateFP(key, fp);

		for(int i = 0; i < MAX_VALID_COUNTER; ++i)
			if(buckets[pos].key[i] == fp)
				return buckets[pos].val[i];

		return 0;
	}


/* interface */
	int get_memory_usage()
	{
		return bucket_num * sizeof(Bucket);
	}
	int get_bucket_num()
	{
		return bucket_num;
	}

private:
	int CalculateFP(uint8_t *key, uint32_t &fp)
	{
		fp = *((uint32_t*)key);
		return CalculateBucketPos(fp) % bucket_num;
	}
};

#endif