数据结构笔记7 二叉树的遍历（先序遍历 中序遍历 后序遍历 层序遍历）

（笔记总结自浙江大学数据结构）

先序遍历

遍历过程为：
① 访问根结点；② 先序遍历其左子树； ③ 先序遍历其右子树。

void PreOrderTraversal( BinTree BT ) {
 if( BT ) {
 printf(“%d”, BT->Data);
 PreOrderTraversal( BT->Left );
 PreOrderTraversal( BT->Right );  
 } }

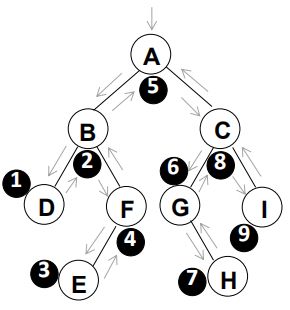
A（B D F E ）（C G H I）
先序遍历=> A B D F E C G H I

中序遍历

遍历过程为：
① 中序遍历其左子树； ② 访问根结点； ③ 中序遍历其右子树。

void InOrderTraversal( BinTree BT ) {
 if( BT ) {
 InOrderTraversal( BT->Left );
 printf(“%d”, BT->Data);
 InOrderTraversal( BT->Right );
 } }

（D B E F） A （G H C I）
中序遍历=> D B E F A G H C I

举例：中序遍历非递归遍历算法
遇到一个结点，就把它压栈，并去遍历它的左子树；
当左子树遍历结束后，从栈顶弹出这个结点并访问它；
然后按其右指针再去中序遍历该结点的右子树。

void InOrderTraversal( BinTree BT ) { BinTree T=BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ){
 while(T){ /*一直向左并将沿途结点压入堆栈*/
 Push(S,T);
 T = T->Left;
 }
 if(!IsEmpty(S)){
 T = Pop(S); /*结点弹出堆栈*/
 printf(“%5d”, T->Data); /*（访问）打印结点*/
 T = T->Right; /*转向右子树*/
 } } }

后序遍历

遍历过程为：
① 后序遍历其左子树； ② 后序遍历其右子树； ③ 访问根结点。

void PostOrderTraversal( BinTree BT ) {
 if( BT ) {
 PostOrderTraversal( BT->Left );
 PostOrderTraversal( BT->Right);
 printf(“%d”, BT->Data);
 } }

（D E F B ）（ H G I C） A
后序遍历=> D E F B H G I C A

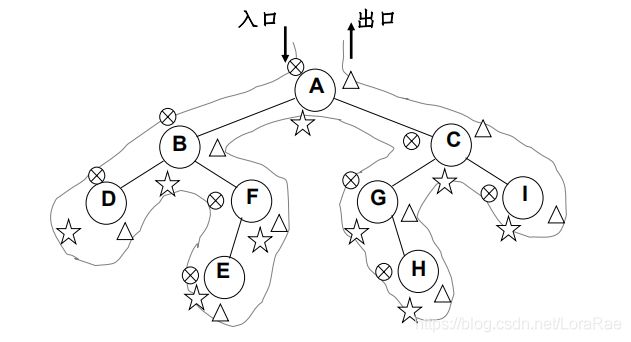
先序、中序和后序遍历过程：遍历过程中经过结点的路线一样，只是访问各结点的时机不同。
图中在从入口到出口的曲线上用×、★ 和△三种符号分别标记出了先序、中序和后序访问各结点的时刻。

前中后源代码汇总：

void InorderTraversal( BinTree BT )
{
    if( BT ) {
        InorderTraversal( BT->Left );
        /* 此处假设对BT结点的访问就是打印数据 */
        printf("%d ", BT->Data); /* 假设数据为整型 */
        InorderTraversal( BT->Right );
    }
}
 
void PreorderTraversal( BinTree BT )
{
    if( BT ) {
        printf("%d ", BT->Data );
        PreorderTraversal( BT->Left );
        PreorderTraversal( BT->Right );
    }
}
 
void PostorderTraversal( BinTree BT )
{
    if( BT ) {
        PostorderTraversal( BT->Left );
        PostorderTraversal( BT->Right );
        printf("%d ", BT->Data);
    }
}
 
void LevelorderTraversal ( BinTree BT )
{ 
    Queue Q; 
    BinTree T;
 
    if ( !BT ) return; /* 若是空树则直接返回 */
     
    Q = CreatQueue(); /* 创建空队列Q */
    AddQ( Q, BT );
    while ( !IsEmpty(Q) ) {
        T = DeleteQ( Q );
        printf("%d ", T->Data); /* 访问取出队列的结点 */
        if ( T->Left )   AddQ( Q, T->Left );
        if ( T->Right )  AddQ( Q, T->Right );
    }
}

层序遍历

二叉树遍历的核心问题：二维结构的线性化
队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点出队、访问该结点、其左右儿子入队


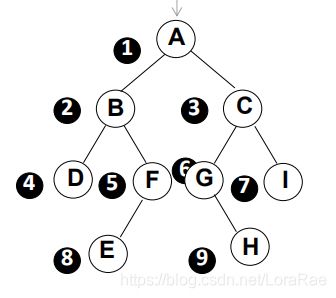
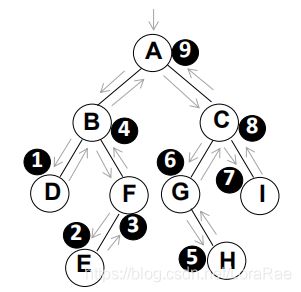
层序遍历 =>A B C D F G I E H

层序基本过程：先根结点入队，然后：
1.从队列中取出一个元素；
2.访问该元素所指结点；
3.若该元素所指结点的左、右孩子结点非空，则将其左、右孩子的指针顺序入队。

void LevelOrderTraversal ( BinTree BT ) { Queue Q; BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */ 
Q = CreatQueue( MaxSize ); /*创建并初始化队列Q*/
AddQ( Q, BT );
while ( !IsEmptyQ( Q ) ) {
 T = DeleteQ( Q );
printf(“%d\n”, T->Data); /*访问取出队列的结点*/
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right ); } }

遍历应用例子

【例】遍历二叉树的应用：输出二叉树中的叶子结点。
在二叉树的遍历算法中增加检测结点的“左右子树是否都为空”。

void PreOrderPrintLeaves( BinTree BT ) {
 if( BT ) {
 if ( !BT-Left && !BT->Right )
 printf(“%d”, BT->Data );
 PreOrderPrintLeaves ( BT->Left );
 PreOrderPrintLeaves ( BT->Right );
 } }

【例】求二叉树的高度。
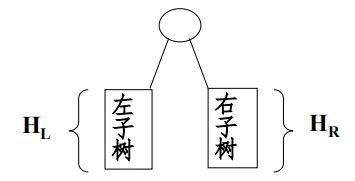Height=max(H_L, H_R)+1

int PostOrderGetHeight( BinTree BT ) { int HL, HR, MaxH;
 if( BT ) {
 HL = PostOrderGetHeight(BT->Left); /*求左子树的深度*/
 HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/
 MaxH = （HL > HR）? HL : HR; /*取左右子树较大的深度*/
 return ( MaxH + 1 ); /*返回树的深度*/
 }
 else return 0; /* 空树深度为0 */
}

【例】 二元运算表达式树及其遍历

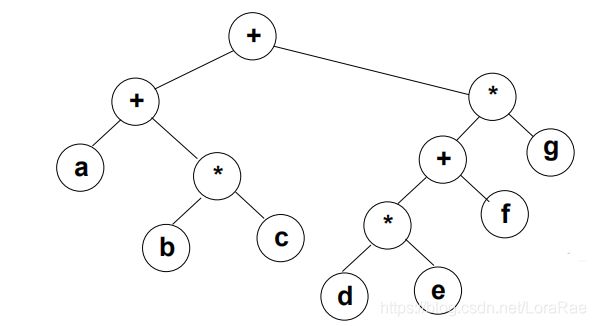
三种遍历可以得到三种不同的访问结果：
先序遍历得到前缀表达式：+ + a * b c * + * d e f g
中序遍历得到中缀表达式：a + b * c + d * e + f * g（中缀表达式会受到运算符优先级的影响）
后序遍历得到后缀表达式：a b c * + d e * f + g * +

【例】 由两种遍历序列确定二叉树
（必须要有中序遍历）

先序和中序遍历序列来确定一棵二叉树：
1 根据先序遍历序列第一个结点确定根结点；
2 根据根结点在中序遍历序列中分割出左右两个子序列；
3 对左子树和右子树分别递归使用相同的方法继续分解。

类似地，后序和中序遍历序列也可以确定一棵二叉树。

问：假定只有四个结点A、B、C、D的二叉树，其前序遍历序列为ABCD，则下面哪个序列是不可能的中序遍历序列？（D）
A.ABCD
B.ACDB
C.DCBA
D.DABC
（D选项，首先根据中序，A在中间，所以左子树的节点只有一个D，而右子树节点是B和C，但根据前序遍历的规则，打印出A以后应该接着打印B，但若D在左子树，B在右子树，则前序遍历不可能先打印出B再打印出D。）