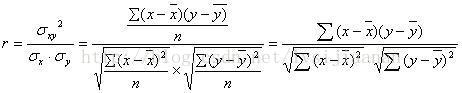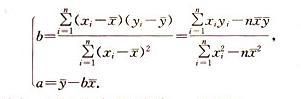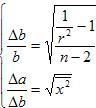线性回归

刚接触此内容，纯小白一个，借鉴网络，有误的内容欢迎指正。

线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。分析按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

一、可以要求误差平方的总和为最小，做为决定理想的线性方程式的准则，这样的方法就称为最小平方误差(least squares error)或是线性回归。MATLAB的polyfit函数提供了 从一阶到高阶多阶式的回归法，其语法为polyfit(x,y,n)，其中x,y为输入数据组n为多项式的阶数，n=1就是一阶 的线性回归法。polyfit函数所建立的多项式可以写成

从polyfit函数得到的输出值就是上述的各项系数，以一阶线性回归为例n=1，所以只有 二个输出值。如果指令为coef=polyfit(x,y,n)，则coef(1)= , coef(2)=,...,coef(n+1)= 。注意上式对n 阶的多 项式会有 n+1 项的系数。看以下的线性回归的示范：

>> x=[0 1 2 3 4 5];

>> y=[0 20 60 68 77 110];

>> coef=polyfit(x,y,1); % coef 代表线性回归的二个输出值

>> a0=coef(1); a1=coef(2);

>> ybest=a0*x+a1; % 由线性回归产生的一阶方程式

>> sum_sq=sum((y-ybest).^2); % 误差平方总合为 356.82

>> axis([-1,6,-20,120])

>> plot(x,ybest,x,y,'o'), title('Linear regression estimate'), grid

二、线性回归拟合方程

最小二乘法：一般来说，线性回归都可以通过最小二乘法求出其方程，可以计算出对于y=bx+a的直线，其经验拟合方程如下：其相关系数（即通常说的拟合的好坏）可以用以下公式来计算：

回归系数：一般要求这个值大于0.05

三、回归误差

因为线性回归是直接计算的，误差可以确定。

四、Python环境下的8种简单线性回归算法

在机器学习中，Scikit-learn 是一个十分流行的 Python 库，人们经常会从这个库调用线性模型来拟合数据。除此之外，我们还可以使用该库的 pipeline 与 FeatureUnion 功能（如：数据归一化、模型回归系数正则化、将线性模型传递给下游模型），但是一般来看，如果一个数据分析师仅需要一个又快又简单的方法来确定回归系数（或是一些相关的统计学基本结果），那么这并不是最快或最简洁的方法。

SciPy 基于 Numpy 建立，集合了数学算法与方便易用的函数。通过为用户提供高级命令，以及用于操作和可视化数据的类，SciPy 显著增强了 Python 的交互式会话。

方法 1：Scipy.polyfit( ) 或 numpy.polyfit( )

numpy.ployfit(x,y,deg,rcond=None,full=False,w=None,cov=False)

这是一个非常一般的最小二乘多项式拟合函数，它适用于任何 degree 的数据集与多项式函数（具体由用户来指定），其返回值是一个（最小化方差）回归系数的数组。

对于简单的线性回归而言，你可以把 degree 设为 1。如果你想拟合一个 degree 更高的模型，你也可以通过从线性特征数据中建立多项式特征来完成。

方法 2：stats.linregress( )

stats.linregress(x,y=None)

这是 Scipy 中的统计模块中的一个高度专门化的线性回归函数。其灵活性相当受限，因为它只对计算两组测量值的最小二乘回归进行优化。因此，你不能用它拟合一般的线性模型，或者是用它来进行多变量回归分析。但是，由于该函数的目的是为了执行专门的任务，所以当我们遇到简单的线性回归分析时，这是最快速的方法之一。除了已拟合的系数和截距项（intercept term）外，它还会返回基本的统计学值如 R² 系数与标准差。

方法 3：optimize.curve_fit( )

scipy.optimize.curve_fit(f,xdata,ydata,p0=None,sigma=None,absojac=None,**kwargs)

这个方法与 Polyfit 方法类似，但是从根本来讲更为普遍。通过进行最小二乘极小化，这个来自 scipy.optimize 模块的强大函数可以通过最小二乘方法将用户定义的任何函数拟合到数据集上。

对于简单的线性回归任务，我们可以写一个线性函数：mx+c，我们将它称为估计器。它也适用于多变量回归。它会返回一个由函数参数组成的数列，这些参数是使最小二乘值最小化的参数，以及相关协方差矩阵的参数。

方法 4：numpy.linalg.lstsq

numpy.linalg.lstsq(a,b,recond=-1)

这是用矩阵因式分解来计算线性方程组的最小二乘解的根本方法。它来自 numpy 包中的线性代数模块。通过求解一个 x 向量（它将|| b—a x ||²的欧几里得 2-范数最小化），它可以解方程 ax=b。

该方程可能会欠定、确定或超定（即，a 中线性独立的行少于、等于或大于其线性独立的列数）。如果 a 是既是一个方阵也是一个满秩矩阵，那么向量 x（如果没有舍入误差）正是方程的解。

借助这个方法，你既可以进行简单变量回归又可以进行多变量回归。你可以返回计算的系数与残差。一个小窍门是，在调用这个函数之前，你必须要在 x 数据上附加一列 1，才能计算截距项。结果显示，这是处理线性回归问题最快速的方法之一。

方法 5： Statsmodels.OLS ( )

statsmodel 是一个很不错的 Python 包，它为人们提供了各种类与函数，用于进行很多不同统计模型的估计、统计试验，以及统计数据研究。每个估计器会有一个收集了大量统计数据结果的列表。其中会对结果用已有的统计包进行对比试验，以保证准确性。

对于线性回归，人们可以从这个包调用 OLS 或者是 Ordinary least squares 函数来得出估计过程的最终统计数据。

需要记住的一个小窍门是，你必须要手动为数据 x 添加一个常数，以用于计算截距。否则，只会默认输出回归系数。下方表格汇总了 OLS 模型全部的结果。它和任何函数统计语言（如 R 和 Julia）一样丰富。

方法 6、7：使用矩阵求逆方法的解析解

对于一个良态（well-conditioned）线性回归问题（至少是对于数据点、特征），回归系数的计算存在一个封闭型的矩阵解（它保证了最小二乘的最小化）。他由下面方程给出：

β=(X的转置*X)的逆*X的转置*y

在这里，我们有两个选择：

方法 6：使用简单矩阵求逆乘法。

方法 7：首先计算数据 x 的广义 Moore-Penrose 伪逆矩阵，然后将结果与 y 进行点积。由于这里第二个步骤涉及到奇异值分解（SVD），所以它在处理非良态数据集的时候虽然速度慢，但是结果不错。（参考：开发者必读：计算机科学中的线性代数）

方法 8： sklearn.linear_model.LinearRegression( )

这个方法经常被大部分机器学习工程师与数据科学家使用。然而，对于真实世界的问题，它的使用范围可能没那么广，我们可以用交叉验证与正则化算法比如 Lasso 回归和 Ridge 回归来代替它。但是要知道，那些高级函数的本质核心还是从属于这个模型。