【cpg控制】HOPF振荡器动态特性分析

零、概述

众所周知，动物最常见的运动方式是节律运动，即按照一定的节奏、有力度地重复、协调、持续进行的动作，是低级神经中枢的自激行为。生物学上，动物的节律运动控制区被认为是分层并且模块化的，其控制以中枢模式发生器为中心，既可以接受来自高层的高级神经中枢的主观控制，也可以响应来自躯体各种感受器官的反射，这就是CPG控制机理。

前人已经按照CPG控制机理建立了不同形式的数学模型，它们能够产生的周期振荡的信号，使其能够满足节律运动的特点。

CPG模型分类
目前比较经典的CPG模型可划分为以下两大类：

• ①基于神经元的模型：Matsuoka神经元震荡模型、Kimura模型等，该类模型生物学意义明确，但参数较多，动态特性分析比较复杂。

• ②基于非线性振荡器的模型：Kuramoto相位振荡器、Hopf谐波振荡器等，该类模型参数较少，模型比较成熟。

在保证能够输出稳定的周期性震荡信号的前提下，那些形式简单、参数较少、计算量小、便于分析、易于实现的CPG模型是更好的选择。根据这一个原则，我们选取了HOPF振荡器作为CPG控制的核心。

一、HOPF振荡器

HOPF振荡器在状态空间中存在一个稳定的极限环，即对于任意非零初始值，均能使得振荡器产生相同形状的周期性振荡信号，其数学模型如下：
$$\frac{dx}{dt}=\alpha (\mu -r^2)x-\omega y$$

$$\frac{dy}{dt}=\alpha (\mu -r^2)y+\omega x$$

其中$\alpha ,\mu ,\omega$为模型参数，用于调整振荡器的动态特性，稍后会给大家演示。现在取$\alpha =100,\mu =1,\omega =2\pi$，我们看下振荡器的输出情况。

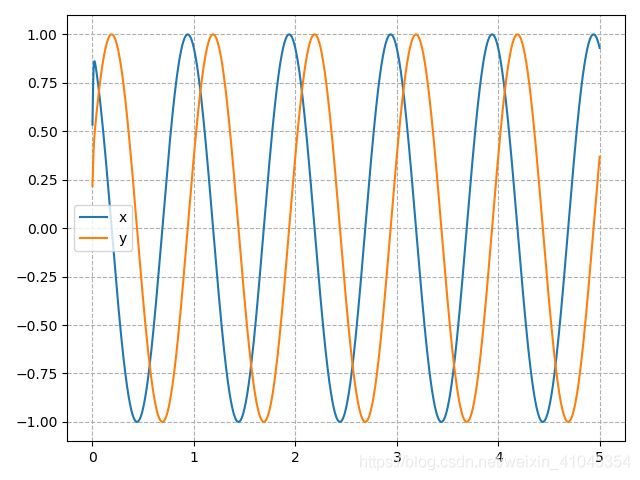
对于给定初始值为[1, 0]，按时间输出，我们能得到以上效果，按x，y输出，我们得到的是一个圆，所以hopf振荡器的输出信号本质上，我们可以看做是一个圆上的点随时间沿圆周运动，

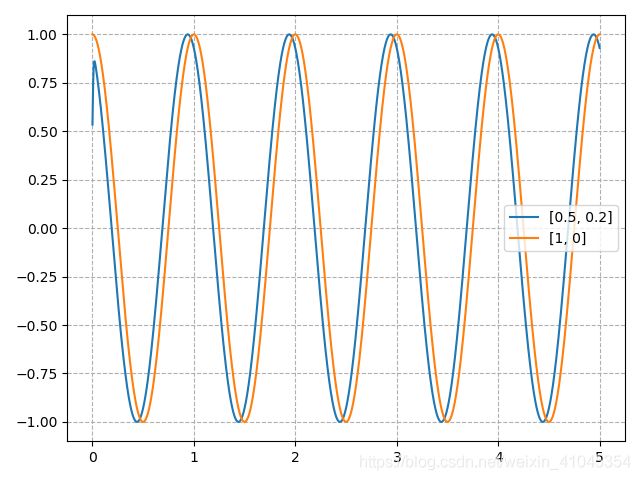
我们尝试一下将初始值点定在圆周外任一点，如[0.5, 0.2]，看下效果：

对比初始值在圆上的曲线，我们可以发现，对于不同初始值的，在稳态输出后仍能收敛到圆上，得到相同波形。这也是我们选择HOPF振荡器作为该四足机器人cpg控制核心的一个重要原因之一。

注意：这里只画出了x值的曲线

二、动态特性

上文已经提到，hopf振荡器有以下参数$\alpha ,\mu ,\omega$，这些参数到底约束了什么，我们一个一个来看。

1、$\alpha$值

该值是用来表征振荡器收敛到圆环上的速度的，我们试着对比不同取值，看波形有什么变化，其余参数均保持一致，取$\mu =1,\omega =2\pi$。初始值设置为[0.5，0]

①分别设置参数$\alpha =10$ ，$\alpha =100$， $\alpha =1000$：

可以看出，$\alpha$值越大时，hopf振荡器越快得到稳定的波形。当该值比较小时，振荡器需要经过很长一段时间才能得到稳态输出，而当其很大时，虽然能够迅速得到稳定的输出，但在收敛阶段产生的信号会非常尖锐，甚至会超过规定的幅值，实际使用中可能会对执行器造成一定损害，所以我们应该根据执行器的特性选取适当的$\alpha$值。

2、$\mu$值

该值是用来表征信号幅值的，即圆环半径。分别取$\mu =0.1，0.5，2$，以$\mu =1$为基准进行比较，其余参数均保持一致，分别为$\alpha =100,\omega =2\pi$， 初始值为[1， 0]

① 设置$\mu =0.25$时：

② 设置$\mu =4$：

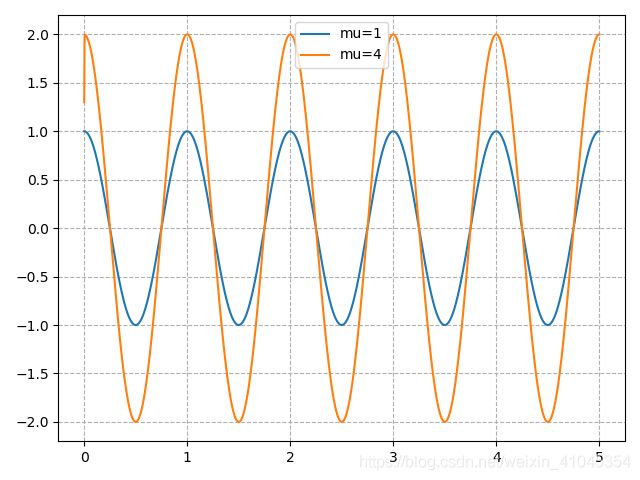
有小伙伴可能会奇怪，为什么要取0.25和4这种相对比较特殊的值，我们通过图像不难发现，$\mu =0.25$时，幅值为0.5。$\mu =4$时，幅值为2，这实际上是一个开方的关系。即幅值$A=\sqrt{\mu }$

3、$\omega$值

该值用来表征周期，计算公式为$T=\frac{2\pi }{\omega }$，同理，我们设置不同取值（$\omega =\pi$，及$\omega =2\pi$），看图像有何区别

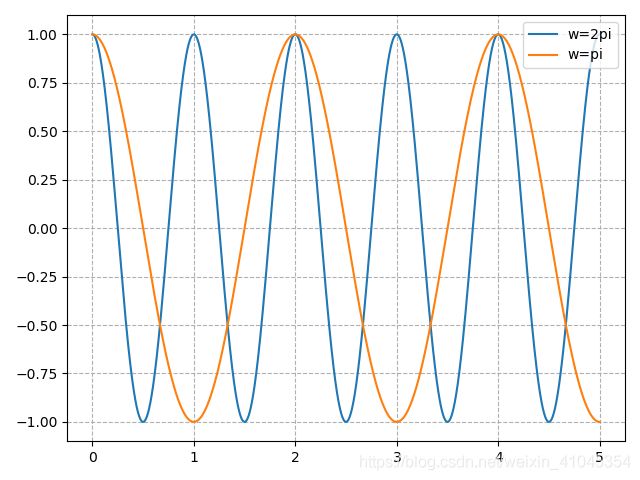
通过控制周期，可以改变信号变化的速度，话句话说，就是我们可以通过$\omega$值来控制机器人的前进速度

---

如果觉得ok，点个赞，点个关注，也欢迎给个打赏支持一下编者的工作