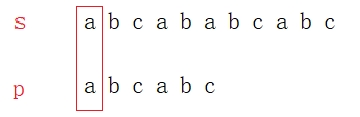- 学习111
麋鹿叔叔
学习
项目名称项目简介主要功能技术原理GitHub地址browser-use智能浏览器工具,让AI像人类一样操作浏览器,实现网页自动化网页浏览与操作、多标签页管理、视觉识别与内容提取、操作记录与重复执行、自定义动作支持、主流LLM模型支持为大语言模型服务的创新Python工具库GitHubEkoFellouAI推出的生产就绪型JavaScript框架,基于自然语言驱动创建智能代理支持所有平台,提供统一便
- 不用再当“技术宅“!这个AI神器让我5分钟变身人工智能达人
阳光永恒736
AI工具人工智能deepseek一键包本地部署AI资源
最近我在朋友圈刷到好多朋友都在玩AI画图、AI写诗,看得我心痒痒。可每次想自己试试,打开教程就被满屏的代码吓退——"Python环境配置"、"CUDA驱动安装"这些词比数学作业还让人头疼。直到我发现了一个叫DeepSeek本地部署一键包的神器,我的AI探索之旅终于变得像搭乐高一样简单!夸克网盘分享一、原来AI离我们这么近上周三放学路上,我看见隔壁班的小美用AI给自己照片生成古风造型,这让我突然意识
- 创建Datas
一一代码
python
核心数据结构创建DataFrame```pythonimportpandasaspd#从字典创建DataFramedata={'Name':['Alice','Bob','Charlie'],'Age':[25,30,35],'City':['NewYork','LosAngeles','Chicago']}df=pd.DataFrame(data)print(df)```输出:```NameAg
- 【免费】2000-2019年各省地方财政企业所得税数据
2501_90487648
数据#省份省地方财政企业所得税
2000-2019年各省地方财政企业所得税数据1、时间:2000-2019年2、来源:国家统计局、统计年鉴3、指标:行政区划代码、地区、年份、地方财政企业所得税4、范围:31省5、指标说明:企业所得税是对企业的利润征收的一种税种,是地方财政收入的重要组成部分之一。企业所得税在地方财政中占有重要位置,通过合理的税收政策和管理,能够有效促进地方经济的健康发展与财政收入的增加。5、下载链接:2000-2
- 3.19学习总结
2402_88131930
学习
学习了Java中的面向对象的知识点完成一道算法题,找树左下角的值,错误的以为左下角只能是最底层的左节点,但指的是最底层最左边的节点
- HTTP请求过程详解
酥暮沐
http网络协议网络
一、整体流程概述HTTP请求过程从用户输入URL开始,到页面完成渲染结束,主要分为DNS解析、建立连接、发送请求、处理响应、渲染页面、断开连接六个核心阶段。重要:当用户输入URL后,浏览器首先解析域名,通过DNS查询获取服务器IP。接着通过三次握手建立TCP连接,如果是HTTPS还会进行TLS加密协商。然后浏览器发送HTTP请求,服务器处理后返回响应数据。浏览器解析HTML/CSS,构建DOM和渲
- 【从零开始学习JAVA】异常体系介绍
Cools0613
从0开始学Java学习
前言:本文我们将为大家介绍一下异常的整个体系,而我们学习异常,不是为了敲代码的时候不出异常,而是为了能够熟练的处理异常,如何解决代码中的异常。异常的两大分类:我们就以这张图作为线索来详细介绍一下Java中的异常:1.Exceptions(异常)在Java中,Exception(异常)是一种表示非致命错误或异常情况的类或接口。Exception通常是由应用程序引发的,可以被程序员捕获、处理或抛出。E
- k8s主要控制器简述(一)ReplicaSet与Deployment
小刘爱喇石( ˝ᗢ̈˝ )
kubernetes容器云原生
目录一、ReplicaSet关键特性示例解释支持的Operator二、Deployment1.声明式更新示例2.滚动更新示例3.回滚示例4.ReplicaSet管理示例5.自动恢复示例6.扩展和缩容示例示例一、ReplicaSetReplicaSet是Kubernetes中的一个核心控制器,用于确保指定数量的Pod副本始终处于运行状态。它的主要职责是维护一组稳定的Pod副本,确保在任何时候都有指定
- Umi-OCR 实践教程:离线、免费、高效的图像文字识别工具
几道之旅
人工智能智能体及数字员工ocr人工智能
一、工具简介Umi-OCR是一款开源、免费且支持离线运行的OCR(光学字符识别)工具,适用于Windows和Linux系统。它基于深度学习技术,能够高效提取图像中的文字,支持多语言识别、批量处理、截屏识别等功能,尤其适合对隐私敏感或网络受限的场景。核心亮点:离线运行:无需联网,保护隐私。多引擎支持:提供Paddle(高性能)和Rapid(低配兼容)两种引擎。批量处理:支持图片、PDF、电子书等多格
- 经典DP——夜狼
_gxd_
DPc++数据结构
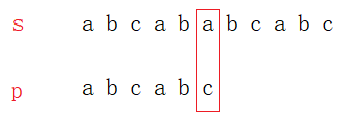
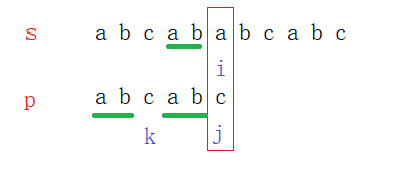
Description夜狼,也被称为黑狼,是非常大型的有力量的狼。据说大部分夜狼起源于德拉诺。夜狼看起来像普通的狼,但这些生物的大小几乎是普通狼的两倍。这些强大的野兽,长8-9尺,重600-800磅,是最有名的兽人坐骑。这些狼和人一样高,长着长牙,看起来像是能咬断铁棍一样。他们有火红色的眼睛,皮毛则是斑驳的黑色或灰色。野狼一般在卡利姆多和穆尔戈尔北部地区繁衍生息。夜狼是高效的猎群者,他们捕杀任何猎
- 使用LangChain实现基于LLM和RAG的PDF问答系统
张同学吧
langchain语言模型
目录前言一.大语言模型(LLM)1.什么是LLM?2.LLM的能力与特点二、增强检索生成(RAG)三.什么是LangChain?1.LangChain的核心功能2.LangChain的优势3.LangChain的应用场景4.总结四.使用LangChain实现基于PDF的问答系统前言本文将介绍LLM和RAG的基本概念,并通过一个实际的代码示例,展示如何使用LangChain构建一个基于PDF文档的问
- python将网银web工程转换成客户端electron工程案例
银行金融科技
人工智能机器学习DeepSeekelectron
以下是一个将网银Web工程转换为Electron客户端的技术方案,结合Python和Electron实现桌面端增强功能:bash#项目结构webank-electron/├──main/#Electron主进程代码│├──main.js│└──python_server.py├──renderer/#网页渲染进程│└──webank-web/#原始网银Web工程├──package.json└──
- 基于ChatGPT、GIS与Python机器学习的地质灾害风险评估、易发性分析、信息化建库及灾后重建高级实践
weixin_贾
防洪评价风险评估滑坡泥石流地质灾害
第一章、ChatGPT、DeepSeek大语言模型提示词与地质灾害基础及平台介绍【基础实践篇】1、什么是大模型?大模型(LargeLanguageModel,LLM)是一种基于深度学习技术的大规模自然语言处理模型。代表性大模型:GPT-4、BERT、T5、ChatGPT等。特点:多任务能力:可以完成文本生成、分类、翻译、问答等任务。上下文理解:能理解复杂的上下文信息。广泛适配性:适合科研、教育、行
- 输了,腾讯golang一面凉了
golang学习记
golanggolang
本月正值4月,是金三银四的找工作的最佳时机。同时竞争也是很大,因为每年这个时候快要毕业的大学生也进去了找工作的潮水中。今天分享我的一位大佬朋友CC,勇闯腾讯golang的面试经历。这次面试问题的方向主要集中在计算机基础个网络方面。下面是主要问到的问题。第一个,http握手,https证书第二个,操作系统的中断,堆和栈第三个,数据库,乐观锁,悲观锁,acid等TSL四次握手的过程是什么第一次握手首先
- 未来已来,把握机会,从DBA到DBA²⓵不幸的DBA各有各的不幸
梁敬彬
AIdba数据库
引言老马是某大公司的资深DBA,某天公司忽然通知裁员,他和徒弟阿牛双双被解雇。半年过去,老马仍未找到工作,而阿牛虽说找到新东家,却只能接受薪资减半的现实。阿牛的同学大黄,同为DBA,虽未经历裁员风波,却因繁重的工作任务倍感压力,老板不但不肯再招人,还对他的表现颇有不满。新人小羊,则因在工作中频频犯错,被公司以低绩效为由辞退。他们都对自己的未来感到迷茫、慌张。⓵不幸的DBA各有各的不幸老马:我现在真
- SQL优化思想——不优化或许是最好的优化⓵哈哈,其实我几乎什么都没做
梁敬彬
sql数据库
引言熟悉我的朋友知道我擅长SQL优化,出版过近80万字的技术书籍——《收获,不止SQL优化》,十余次印刷,反响热烈,在此,感谢支持我的读者。接下来,我将站在SQL优化思想的角度,给大家做一个系列分享。首先就是要有批判性思维,我将告诉大家:不优化或许是最好的优化!故事从L老师的一次优化经历说起,希望给大家带来新的启发。⓵啥没做就搞定Q:L老师,自从您为XXX平台做了SQL优化后,运行非常顺畅,您是做
- OpenAI Deep Research 要 200 美元/月?试试这 4 款免费开源平替!
surfirst
LLM人工智能开源DeepResearch
引言随着AI研究代理(AIresearchagents)的兴起,越来越多的工具能够帮助用户快速获取信息、整理研究报告。OpenAI最近推出的DeepResearch便是一个典型代表,它能在几十分钟内完成原本需要人类数小时的多步骤研究任务。然而,DeepResearch并非唯一的选择,开源社区也提供了多个优秀的替代方案。如果你希望使用开源方案、获得更强的可定制性,或者避免依赖OpenAI,那么本文介
- DeepSeek API在AutoCAD中的创新应用与挑战
CodeJourney.
数据库算法人工智能
在数字化设计领域,随着人工智能技术的飞速发展,将AI能力融入传统设计软件成为提升设计效率和质量的重要趋势。AutoCAD作为广泛应用的计算机辅助设计软件,与DeepSeekAPI的结合展现出了巨大的潜力。这种融合不仅为设计工作带来了全新的思路和方法,还在多个方面对设计流程进行了优化和创新。一、DeepSeekAPI赋能AutoCAD的多元应用场景(一)智能设计辅助:让创意快速落地在传统设计过程中,
- golang面经整理(一)(k8s,docker二次开发方向,云原生方向)
gooooer
1024程序员节
笔者在2022年7月份-9月份之间面试了很多golang和k8s相关的面试,主要想从事云原生相关的开发工作,大小公司面试了很多,现将整体面试感受和一些通用的问题做一些整理记录,帮助大家在面试的时候更好的进行准备。最近大环境不好,大厂的岗位也少了不少。主要投递的岗位包含广州、深圳的岗位,面试的是golang工程师相关的岗位,但其实单纯做云原生相关岗位比较少,基本上局限于国内的几朵云,阿里云,华为云,
- 程序员学商务英语之Don‘t jinx it、l have a half mind to do sth、Don‘t change the subject、Quality over quantity..
李匠2024
英文
1463-Don'tjinxit.-别鸟鸦嘴A:Whatifitrainstheweekend?Youknow,theweather'sbeenchangeablethesedays!如果这个周末下雨怎么办?你知道,这些天的天气变化无常!B:Don'tiinxit.i'vespentalotoftimepreparingforthiscamping.lhopeitstaysfineforthewe
- AI 赋能应急管理:ChatGPT、DeepSeek、Grok 的应用探索
一ge科研小菜菜
人工智能人工智能
个人主页:一ge科研小菜鸡-CSDN博客期待您的关注1.引言随着人工智能(AI)技术的快速发展,大语言模型(LLM)在应急管理领域的应用逐步扩大。ChatGPT、DeepSeek、Grok等AI模型凭借强大的文本处理、数据分析和推理能力,可为灾害预警、应急响应、风险评估等提供高效支持。本文将对比三大AI模型在应急管理中的优势,并探讨其在未来智能化应急管理体系中的应用前景。2.应急管理中的核心挑战应
- android sqlite 数据库简单封装示例(java)
mmsx
android作业源码分享java数据库android
sqlite数据库简单封装示例,使用记事本数据库表进行示例。首先继承SQLiteOpenHelper使用sql语句进行创建一张表。publicclassnoteDBHelperextendsSQLiteOpenHelper{publicnoteDBHelper(Contextcontext,Stringname,SQLiteDatabase.CursorFactoryfactory,intvers
- 华为静音模式指定联系人来电响铃
修心光
智能手机
华为静音模式指定联系人来电响铃本人7年水果转华为,手机常年静音但是还是想收到指定人来电的。水果这个地方做的是很方便的,直接添加紧急联系人,什么声音都没有,只有指定人的电话铃声直接上结论,华为是不支持直接这样设置的,也就是水果里面静音后,打开紧急联系人,仍能收到电话的功能,鸿蒙现在没有,但是有一些间接实现的办法一个不算完美但有用的常见解决方案:在上看了一些方法,比较有效的办法是全天开免打扰,然后设置
- 前端如何实现一个五星评价,鼠标滑动,前边星星颜色的变黄,后边的不变;
修心光
前端
直接上代码.star-rating{display:flex;padding:10px0;}.star{position:relative;width:40px;height:40px;}.half{position:absolute;top:0;width:20px;height:40px;overflow:hidden;font-size:40px;color:#e0e0e0;cursor:p
- 【元婴境】mysql的MVCC(详解)
jstart千语
mysql数据库
目录MVCC介绍隐藏字段undologReadView示例:流程总结MVCC介绍大家好,我是jstart千语。上篇我们讲到mysql的事务隔离级别,其中MVCC就是控制事务隔离级别的重要组成部分,也是实现事务四大特性之一隔离性的重要手段。那么接下来我将通透地讲解MVCC,让大家对mysql的隔离性有一个更深刻的理解。MVCC全称Multi-VersionConcurrencyControl,也就是
- cmake makefile cmakelists.txt的区别和联系
YRr YRr
CMakec++开发语言cmake
cmakemakefilecmakelists.txt的区别和联系理解CMake、Makefile和CMakeLists.txt的区别和联系,可以帮助我们更好地管理和构建C/C++项目。Makefile(GNUMake):定义与作用:Makefile是一种文本文件,通常用于指定如何编译和链接源代码以生成可执行文件或库文件。它包含了一系列规则(rules),每个规则指定了如何生成一个或多个目标文件(
- Git如何将一个分支上的修改转移到另一个分支
风继续吹..
Git基本指令git
在我们使用git进行版本控制时,当代码写错分支,怎么将这些修改转移到正确的分支上去呢?这时,我们可以使用gitstath命令来暂存我们的修改,然后再切换到其他分支未commit(提交)操作时1.先将修改存入暂存区gitadd.2.把暂存区内的修改存储起来gitstash3.切换到正确的分支gitcheckoutdev4.将存储的修改取出来gitstashpop已commit(提交)操作时需要撤回c
- 拥抱健康养生,畅享美好生活
lanlande33
生活
在快节奏的现代生活中,健康养生已成为我们追求高品质生活的关键。它并非遥不可及的高深学问,而是融入在日常的点点滴滴,是一种积极的生活态度,能让我们身心愉悦,活力满满。合理饮食是健康养生的基石。多吃新鲜蔬果,它们富含维生素、矿物质与膳食纤维,像橙子能提供丰富维C,增强免疫力;芹菜则促进肠道蠕动,预防便秘。粗粮也不可少,燕麦、糙米等能缓慢释放能量,让我们保持充沛精力。减少高油高糖高盐食物的摄入,炸鸡、蛋
- 拥抱健康养生,开启活力生活
lanlande33
生活
在快节奏的现代社会,人们在忙碌奔波中,常常忽略了自身的健康。健康养生,绝非一时的潮流,而是关乎我们生活品质与生命长度的关键。它宛如一座灯塔,照亮我们追求身心和谐的道路。合理饮食是健康养生的基石。《黄帝内经》讲:“五谷为养,五果为助,五畜为益,五菜为充。”我们应秉持均衡原则,让各类营养物质在餐桌上巧妙搭配。多摄入富含膳食纤维的蔬果,它们如同肠道的“清道夫”,助力消化,预防疾病;全谷物食品提供持久稳定
- 拥抱健康养生,开启活力生活
lanlande33
生活
在快节奏的现代社会,健康养生不再是一句口号,而是我们对高品质生活的追求。它贯穿于日常的点点滴滴,对我们的身心状态有着深远影响。饮食养生是基础。秉持均衡原则,每日的餐盘应是色彩斑斓的。新鲜蔬菜富含维生素与膳食纤维,像菠菜、西兰花,助力肠道蠕动,维持身体代谢平衡;水果提供丰富果酸与天然糖分,苹果、橙子等,补充水分与营养。优质蛋白质不可或缺,瘦肉、鱼类、豆类都是上佳之选,为身体修复与生长提供原料。同时,
- 继之前的线程循环加到窗口中运行
3213213333332132
javathreadJFrameJPanel
之前写了有关java线程的循环执行和结束,因为想制作成exe文件,想把执行的效果加到窗口上,所以就结合了JFrame和JPanel写了这个程序,这里直接贴出代码,在窗口上运行的效果下面有附图。
package thread;
import java.awt.Graphics;
import java.text.SimpleDateFormat;
import java.util
- linux 常用命令
BlueSkator
linux命令
1.grep
相信这个命令可以说是大家最常用的命令之一了。尤其是查询生产环境的日志,这个命令绝对是必不可少的。
但之前总是习惯于使用 (grep -n 关键字 文件名 )查出关键字以及该关键字所在的行数,然后再用 (sed -n '100,200p' 文件名),去查出该关键字之后的日志内容。
但其实还有更简便的办法,就是用(grep -B n、-A n、-C n 关键
- php heredoc原文档和nowdoc语法
dcj3sjt126com
PHPheredocnowdoc
<!doctype html>
<html lang="en">
<head>
<meta charset="utf-8">
<title>Current To-Do List</title>
</head>
<body>
<?
- overflow的属性
周华华
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- 《我所了解的Java》——总体目录
g21121
java
准备用一年左右时间写一个系列的文章《我所了解的Java》,目录及内容会不断完善及调整。
在编写相关内容时难免出现笔误、代码无法执行、名词理解错误等,请大家及时指出,我会第一时间更正。
&n
- [简单]docx4j常用方法小结
53873039oycg
docx
本代码基于docx4j-3.2.0,在office word 2007上测试通过。代码如下:
import java.io.File;
import java.io.FileInputStream;
import ja
- Spring配置学习
云端月影
spring配置
首先来看一个标准的Spring配置文件 applicationContext.xml
<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.org/schema/beans"
xmlns:xsi=&q
- Java新手入门的30个基本概念三
aijuans
java新手java 入门
17.Java中的每一个类都是从Object类扩展而来的。 18.object类中的equal和toString方法。 equal用于测试一个对象是否同另一个对象相等。 toString返回一个代表该对象的字符串,几乎每一个类都会重载该方法,以便返回当前状态的正确表示.(toString 方法是一个很重要的方法) 19.通用编程:任何类类型的所有值都可以同object类性的变量来代替。
- 《2008 IBM Rational 软件开发高峰论坛会议》小记
antonyup_2006
软件测试敏捷开发项目管理IBM活动
我一直想写些总结,用于交流和备忘,然都没提笔,今以一篇参加活动的感受小记开个头,呵呵!
其实参加《2008 IBM Rational 软件开发高峰论坛会议》是9月4号,那天刚好调休.但接着项目颇为忙,所以今天在中秋佳节的假期里整理了下.
参加这次活动是一个朋友给的一个邀请书,才知道有这样的一个活动,虽然现在项目暂时没用到IBM的解决方案,但觉的参与这样一个活动可以拓宽下视野和相关知识.
- PL/SQL的过程编程,异常,声明变量,PL/SQL块
百合不是茶
PL/SQL的过程编程异常PL/SQL块声明变量
PL/SQL;
过程;
符号;
变量;
PL/SQL块;
输出;
异常;
PL/SQL 是过程语言(Procedural Language)与结构化查询语言(SQL)结合而成的编程语言PL/SQL 是对 SQL 的扩展,sql的执行时每次都要写操作
- Mockito(三)--完整功能介绍
bijian1013
持续集成mockito单元测试
mockito官网:http://code.google.com/p/mockito/,打开documentation可以看到官方最新的文档资料。
一.使用mockito验证行为
//首先要import Mockito
import static org.mockito.Mockito.*;
//mo
- 精通Oracle10编程SQL(8)使用复合数据类型
bijian1013
oracle数据库plsql
/*
*使用复合数据类型
*/
--PL/SQL记录
--定义PL/SQL记录
--自定义PL/SQL记录
DECLARE
TYPE emp_record_type IS RECORD(
name emp.ename%TYPE,
salary emp.sal%TYPE,
dno emp.deptno%TYPE
);
emp_
- 【Linux常用命令一】grep命令
bit1129
Linux常用命令
grep命令格式
grep [option] pattern [file-list]
grep命令用于在指定的文件(一个或者多个,file-list)中查找包含模式串(pattern)的行,[option]用于控制grep命令的查找方式。
pattern可以是普通字符串,也可以是正则表达式,当查找的字符串包含正则表达式字符或者特
- mybatis3入门学习笔记
白糖_
sqlibatisqqjdbc配置管理
MyBatis 的前身就是iBatis,是一个数据持久层(ORM)框架。 MyBatis 是支持普通 SQL 查询,存储过程和高级映射的优秀持久层框架。MyBatis对JDBC进行了一次很浅的封装。
以前也学过iBatis,因为MyBatis是iBatis的升级版本,最初以为改动应该不大,实际结果是MyBatis对配置文件进行了一些大的改动,使整个框架更加方便人性化。
- Linux 命令神器:lsof 入门
ronin47
lsof
lsof是系统管理/安全的尤伯工具。我大多数时候用它来从系统获得与网络连接相关的信息,但那只是这个强大而又鲜为人知的应用的第一步。将这个工具称之为lsof真实名副其实,因为它是指“列出打开文件(lists openfiles)”。而有一点要切记,在Unix中一切(包括网络套接口)都是文件。
有趣的是,lsof也是有着最多
- java实现两个大数相加,可能存在溢出。
bylijinnan
java实现
import java.math.BigInteger;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class BigIntegerAddition {
/**
* 题目:java实现两个大数相加,可能存在溢出。
* 如123456789 + 987654321
- Kettle学习资料分享,附大神用Kettle的一套流程完成对整个数据库迁移方法
Kai_Ge
Kettle
Kettle学习资料分享
Kettle 3.2 使用说明书
目录
概述..........................................................................................................................................7
1.Kettle 资源库管
- [货币与金融]钢之炼金术士
comsci
金融
自古以来,都有一些人在从事炼金术的工作.........但是很少有成功的
那么随着人类在理论物理和工程物理上面取得的一些突破性进展......
炼金术这个古老
- Toast原来也可以多样化
dai_lm
androidtoast
Style 1: 默认
Toast def = Toast.makeText(this, "default", Toast.LENGTH_SHORT);
def.show();
Style 2: 顶部显示
Toast top = Toast.makeText(this, "top", Toast.LENGTH_SHORT);
t
- java数据计算的几种解决方法3
datamachine
javahadoopibatisr-languer
4、iBatis
简单敏捷因此强大的数据计算层。和Hibernate不同,它鼓励写SQL,所以学习成本最低。同时它用最小的代价实现了计算脚本和JAVA代码的解耦,只用20%的代价就实现了hibernate 80%的功能,没实现的20%是计算脚本和数据库的解耦。
复杂计算环境是它的弱项,比如:分布式计算、复杂计算、非数据
- 向网页中插入透明Flash的方法和技巧
dcj3sjt126com
htmlWebFlash
将
Flash 作品插入网页的时候,我们有时候会需要将它设为透明,有时候我们需要在Flash的背面插入一些漂亮的图片,搭配出漂亮的效果……下面我们介绍一些将Flash插入网页中的一些透明的设置技巧。
一、Swf透明、无坐标控制 首先教大家最简单的插入Flash的代码,透明,无坐标控制: 注意wmode="transparent"是控制Flash是否透明
- ios UICollectionView的使用
dcj3sjt126com
UICollectionView的使用有两种方法,一种是继承UICollectionViewController,这个Controller会自带一个UICollectionView;另外一种是作为一个视图放在普通的UIViewController里面。
个人更喜欢第二种。下面采用第二种方式简单介绍一下UICollectionView的使用。
1.UIViewController实现委托,代码如
- Eos平台java公共逻辑
蕃薯耀
Eos平台java公共逻辑Eos平台java公共逻辑
Eos平台java公共逻辑
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月1日 17:20:4
- SpringMVC4零配置--Web上下文配置【MvcConfig】
hanqunfeng
springmvc4
与SpringSecurity的配置类似,spring同样为我们提供了一个实现类WebMvcConfigurationSupport和一个注解@EnableWebMvc以帮助我们减少bean的声明。
applicationContext-MvcConfig.xml
<!-- 启用注解,并定义组件查找规则 ,mvc层只负责扫描@Controller -->
<
- 解决ie和其他浏览器poi下载excel文件名乱码
jackyrong
Excel
使用poi,做传统的excel导出,然后想在浏览器中,让用户选择另存为,保存用户下载的xls文件,这个时候,可能的是在ie下出现乱码(ie,9,10,11),但在firefox,chrome下没乱码,
因此必须综合判断,编写一个工具类:
/**
*
* @Title: pro
- 挥洒泪水的青春
lampcy
编程生活程序员
2015年2月28日,我辞职了,离开了相处一年的触控,转过身--挥洒掉泪水,毅然来到了兄弟连,背负着许多的不解、质疑——”你一个零基础、脑子又不聪明的人,还敢跨行业,选择Unity3D?“,”真是不自量力••••••“,”真是初生牛犊不怕虎•••••“,••••••我只是淡淡一笑,拎着行李----坐上了通向挥洒泪水的青春之地——兄弟连!
这就是我青春的分割线,不后悔,只会去用泪水浇灌——已经来到
- 稳增长之中国股市两点意见-----严控做空,建立涨跌停版停牌重组机制
nannan408
对于股市,我们国家的监管还是有点拼的,但始终拼不过飞流直下的恐慌,为什么呢?
笔者首先支持股市的监管。对于股市越管越荡的现象,笔者认为首先是做空力量超过了股市自身的升力,并且对于跌停停牌重组的快速反应还没建立好,上市公司对于股价下跌没有很好的利好支撑。
我们来看美国和香港是怎么应对股灾的。美国是靠禁止重要股票做空,在
- 动态设置iframe高度(iframe高度自适应)
Rainbow702
JavaScriptiframecontentDocument高度自适应局部刷新
如果需要对画面中的部分区域作局部刷新,大家可能都会想到使用ajax。
但有些情况下,须使用在页面中嵌入一个iframe来作局部刷新。
对于使用iframe的情况,发现有一个问题,就是iframe中的页面的高度可能会很高,但是外面页面并不会被iframe内部页面给撑开,如下面的结构:
<div id="content">
<div id=&quo
- 用Rapael做图表
tntxia
rap
function drawReport(paper,attr,data){
var width = attr.width;
var height = attr.height;
var max = 0;
&nbs
- HTML5 bootstrap2网页兼容(支持IE10以下)
xiaoluode
html5bootstrap
<!DOCTYPE html>
<html>
<head lang="zh-CN">
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">