深度优先搜索（dfs）练习题及详细解答

相信很多人在最先开始学习深度优先搜索（dfs）的时候，都是一脸懵逼，但其实只要通过一定数目的练习，你就可以熟练运用这一算法（骗分神器）了，下面是我挑选出的几道dfs题目（源自洛谷），相信你练习完了以后，对这一神奇算法也会有更深的体会。
首先是一道dfs的入门题：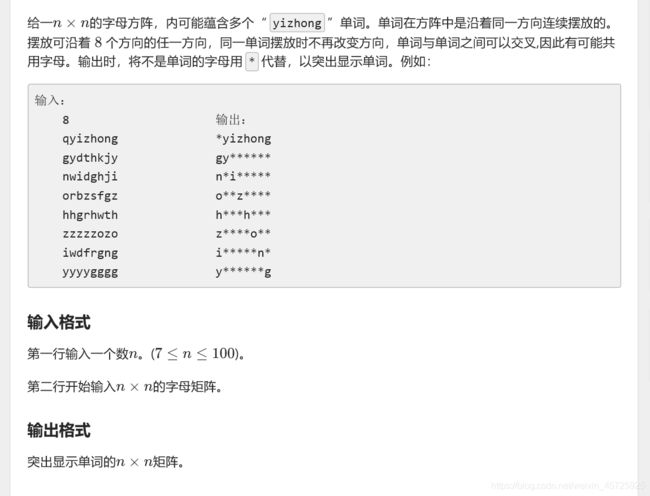
下面是代码

#include//万能头
using namespace std;
char keyword[]="yizhong";
char square[101][101]; //输入数组
char book[101][101];    //记录变化的数组
int drive[8][2]={{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1}};//八方向数组
int n;   //n*n
struct road{    //记录路径的结构体
int x , y;
};
road way[7];    //记录路径
void dfs(int x , int y , int state ,int dir)//dir是方向，搜索的方向，x，y是开始搜索的坐标，state当前搜索到了第几个字母
{ 
   if(state>6){ 
   for(int i = 0 ; i < 7 ; i++)  //如果搜索完了，说明所求的就是想要的
       book[way[i].x][way[i].y] = 1; //记录路径
   }
   else if(state <= 6){ 
   int dx = x + drive[dir][0];
   int dy = y + drive[dir][1];
   if(state == 6 || square[dx][dy] == keyword[state+1]){  //如果state等于6，说明已经搜索完了
   way[state].x = x;    //记录路径
   way[state].y = y;
   dfs(dx,dy,state+1,dir);  //搜索下个节点，如果修改了state的值下面，如state++，下面就要加一行state--，以达到回溯的目的，这里偷懒了，就直接state+1了
   }   
   }
}
int main()
{ 
   cin>>n;
   for(int i = 0 ; i < n ; i++)
       for(int j = 0 ; j < n ; j++){ 
       cin>>square[i][j];
       }
   for(int i = 0 ; i < n ; i++)
       for(int j = 0 ; j < n ; j++){ 
        if(square[i][j] == 'y'){
        for(int k = 0 ; k < 8 ; k++){ 
            if(square[i+drive[k][0]][j+drive[k][1]] == 'i'){ //如果满足条件，开始深搜
            dfs(i,j,0,k);
            }
        }
        } 
       }
   for(int i = 0 ; i < n ; i++){ 
       for(int j = 0 ; j < n ; j++){ 
       if(book[i][j])cout<<square[i][j];  //输出
       else cout<<'*';
       }
       cout<<endl;
   }
   return 0;
}           //总的来说这还是一道不错的入门题

第二题：

题目链接
这道题与上道题有些许不同，这里需要用到一个小的优化，也就是我们常说的剪枝
下面是代码：

#include
using namespace std;
int N , Sum;
bool flag = false;    //记录是否搜索完毕的标志
int ans[20] , bd[20] , book[20];   //分别是储存答案的数组，模板数组，判重数组
int getC(int a , int b)   //获取组合数的函数
{
    int sum = 1;
    if( b > a/2) b = a - b;
    for(int i = 1 ; i <= b ; i++)
    sum = sum * a-- / i;
    return sum;
}
void st(int n)   //初始化的函数，利用杨辉三角形各项系数为相应n-1的组合数，初始化一个模板数组
{
    int sum = 0;
    for(int i = 0 ; i < n ; i++)
    bd[i] = getC(n-1,i);
}
void dfs(int sum , int step) //深搜
{
    if(sum > Sum)return ;   //剪枝，即如果这里的sum比所需要的Sum还要大的话就没有必要搜索下去了
    if(step == N){         //如果满足条件，标记，返回
        if(sum == Sum) flag = true;    
        return;
    }
     for(int i = 1 ; i <= N ; i++)
     {
      if(!book[i]){      //如果没有搜索过
      ans[step] = i;
      book[i] = 1;
      dfs(sum + ans[step] * bd[step] , step + 1);
      if(flag)return;              //这里很重要，如果没有，搜索会继续进行下去
      book[i] = 0;
      }
     }
}
int main()
{
  cin>>N>>Sum;
  st(N);    // for(int i = 0 ; i < N ; i++) cout<
  dfs(0,0);
   if(flag){
   for(int i = 0 ; i < N ; i++)
       cout<<ans[i]<<" ";      //输出答案，结束
   }
  return 0;  
}
这里简单介绍了剪枝，如果不利用这个剪枝，可能会TLE（我没有试过）

第三题：

题目链接：点这里
下面是代码：

#include
using namespace std;
char ans[10] , rec1[10][10] , rec2[10][10];
int t , k , tot; //t为数据组数，k为字典序的位次 ， tot为总共的答案总数
bool appear(char ch , int col)   //判断字母是否再两个矩阵中的同一列中出现的函数
{ 
    bool flag1 = false , flag2 = false;
 for(int i = 0 ; i < 6 ; i++)
     if(rec1[i][col] == ch) flag1 = true;
 for(int i = 0 ; i < 6 ; i++)
     if(rec2[i][col] == ch) flag2 = true;
 if(flag1 && flag2) return true;  //同时成立返回true
    return false;
}
void dfs(int times)   //深搜答案个数
{ 
 if(times == 5){    //搜索到了第五列
    tot++;            // 答案总数加一
 if(k == tot)cout<<ans<<endl;      //如果找到了答案输出
 return;                           //返回
 }
  for(int i = 0 ; i < 26 ; i++){          //从A~Z枚举 可以保证是字典序排列
    if(appear( i + 'A' , times)){ 
     ans[times] = i + 'A';           
     dfs(times+1);     //深搜下一个
    }
  }
}
int main()
{ 
    cin>>t;
    while(t--)        
    { 
    tot = 0 ;
    memset(rec1 , 0 , sizeof(rec1));   
    memset(rec2 , 0 , sizeof(rec2));
    memset(ans , 0 ,sizeof(ans));   //为下一组做好准备
     cin>>k;
      for(int i = 0 ; i < 6 ; i++)
          scanf("%s",&rec1[i]);
      for(int i = 0 ; i < 6 ; i++)
              scanf("%s",&rec2[i]);
      dfs(0);
       if(tot<k) cout<<"NO"<<endl;  //如果答案总数小于k ， 则不可能输出NO
    }
    return 0;
}   

第四题：

题目链接：点这里
下面是代码：

#include
using namespace std;
int n , m , tot_cake;   // n是蛋糕的数目 ， m是人的数目 ， tot_cake是蛋糕的总数量
int need_cake;             //这是需要的蛋糕总量
int size_cake[60] , size_pp[1025] , pre_sum[1025];   //分别是蛋糕的大小，人嘴的大小，人嘴的前缀和
bool flag = false;                //标志是否蛋糕是否足够
void dfs(int numpp , int numcake)   // numpp是0~numpp的嘴是否能够满足 ， numcake是从第numcake开始吃
{
  if(numpp < 0){flag = true; return;}    //如果小于零的话，蛋糕必定吃完了，即标记返回   
   for(int i = numcake ; i < n ; i++){
       if(numpp < 0){flag = true; return;}         //在for循环内部c进行判断，即return和标记
       if(tot_cake < need_cake)return;           //如果蛋糕总数小于所需蛋糕数，直接返回
       if(flag) return;                          //如果已经可以了，直接返回
        if(size_cake[i] >= size_pp[numpp]){         //如果蛋糕的大小大于人口的大小，则开始切蛋糕
        size_cake[i] -= size_pp[numpp];           
        tot_cake -= size_pp[numpp];
        need_cake -= size_pp[numpp];          //切蛋糕
        if(tot_cake<size_pp[0] && numpp != 0)return;  //如果中途出现蛋糕总量会小于人口最小的量并且此时numpp不是0，则此种情况不可能，返回
        if(size_cake[i] < size_pp[0]) tot_cake -= size_cake[i];   //如果蛋糕剩余的量小于最小人口的大小，则这部分的蛋糕为无用蛋糕，直接去除
         if(size_pp[numpp] == size_pp[numpp - 1]) dfs( numpp - 1 , i);    //如果前一个人的嘴的大小和后一个人的大小一样大，可以延续上述蛋糕的变化，直接dfs（numpp-1，i）
         else dfs(numpp - 1 , 0);                                //否则，再从0搜索
          if(size_cake[i] < size_pp[0]) tot_cake += size_cake[i];      //回溯
          size_cake[i] += size_pp[numpp];
          tot_cake += size_pp[numpp];
          need_cake += size_pp[numpp];
      }
   }
}
int main()
{
    cin>>n;
    for(int i = 0 ; i < n ; i++){       //输入
        scanf("%d",&size_cake[i]);
        tot_cake += size_cake[i];
    }
    cin>>m;
    for(int i = 0 ; i < m ; i++)
        scanf("%d",&size_pp[i]);
    sort(size_pp , size_pp + m);
    pre_sum[0] = size_pp[0];   //s初始化前缀和
         for(int i = 1 ; i < m ; i++)
             pre_sum[i] = pre_sum[i-1] + size_pp[i];
    int l = 0 , r = m - 1;
    while(tot_cake<pre_sum[r]) r--;   //优化剪枝，如果总的蛋糕量小于前缀和，则可以缩小右边界
      while(l <= r)       //二分法
      {
         flag = false;     //首先初始化标志为false
         int mid = (l + r) >>1;    //二分
         need_cake = pre_sum[mid];     //需要的蛋糕总量是前缀和
         dfs(mid , 0);             //搜索判断
         if(flag) l = mid + 1;     //如果蛋糕足够的话，左边界右移
         else r = mid - 1;          //如果不够的话，右边界左移
      }
      cout<<l;         //由于这里是从零开始，本来是l-1，这里变成l
      return 0;
}
这道题目细节和所需要的技巧和能力都要求挺高，要想理解需要花费比较大的精力（光是理解别人的这段代码我都花了不少的时间。。没错，我这蒟蒻怎么可能想出来。。）

未完待续。。。