DFS经典题目详解

【洛谷】P1605 迷宫

原题链接：https://www.luogu.com.cn/problem/P1605

• 思路： 简单 dfs，先对地图进行标记，空地和障碍分开标记不同的数字，然后从起始点开始深搜，如果是终点就方案书加 1，否则就向四个方向不断搜索，符合条件就标记搜索，然后回溯。

Code：

import java.util.Scanner;
public class Main {
	static int ans=0,n,m,t,sx,sy,ex,ey;
	static int[][] dir = {{-1,0},{1,0},{0,-1},{0,1}};
	static int[][] maps = new int[10][10];
	static boolean[][] vis = new boolean[10][10];
	static void dfs(int x,int y) {
		if(x==ex && y==ey) {
			ans++;
			return;
		}
		for(int i=0;i<4;i++) {
			int xx = x+dir[i][0];
			int yy = y+dir[i][1];
			if(!vis[xx][yy] && xx>=1 && xx<=n && yy>=1 && yy<=m && maps[xx][yy]==1) {
				vis[xx][yy]=true;
				dfs(xx,yy);
				vis[xx][yy]=false;
			}
		}
	}
	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		n = cin.nextInt(); m = cin.nextInt(); t = cin.nextInt();
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++)
				maps[i][j]=1;
		sx = cin.nextInt(); sy = cin.nextInt(); ex = cin.nextInt(); ey = cin.nextInt();
		while(t-- >0) {
			int x = cin.nextInt(), y = cin.nextInt();
			maps[x][y]=0;
		}
		vis[sx][sy]=true;
		dfs(sx,sy);
		System.out.println(ans);
	}
}

【洛谷】P1101 单词方阵

原题链接：https://www.luogu.com.cn/problem/P1101

• 思路： 先将目标字符串存入数组，遍历整个地图，找到第一个字符时，就向八个方向深搜，符合条件的就不断按这个方向深搜，搜索的过程中把搜索到的坐标存入数组，直到找到最后一个相应的字符，把数组里的字符位置标记。最后遍历一遍地图，把标记的输出原字符，否则输出 “ * ” 。以后搜索题下标都要从 1 开始了，一开始因为从 0 开始导致最后一个样例老是 RE，这道题的数据也是很水。

Code：

import java.util.Scanner;
public class Main {
	static int n;
	static char[] word = {'y','i','z','h','o','n','g'};
	static char[][] ch = new char[150][150];
	static int[] row = new int[150];
	static int[] col = new int[150];
	static int[][] dir = {{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,-1},{1,-1},{-1,1}};
	static boolean[][] vis = new boolean[200][200];
	static boolean check(int x,int y) {
		if(x>=1 && x<=n && y>=1 && y<=n)	return true;
		return false;
	}
	static void dfs(int x,int y,int m,int d) {
		row[m]=x;
		col[m]=y;
		if(m==6) {
			for(int i=0;i<7;i++)
				vis[row[i]][col[i]]=true;
			return;
		}
		if(check(x+dir[d][0],y+dir[d][1]) && m<6 && ch[x][y]==word[m])
			dfs(x+dir[d][0],y+dir[d][1],m+1,d);
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner cin = new Scanner(System.in);
		n = cin.nextInt();
		for(int i=1;i<=n;i++) {
			String str = cin.next();
			for(int j=1;j<=n;j++)
				ch[i][j] = str.charAt(j-1);
		}
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=n;j++) {
				if(ch[i][j]=='y') {
					for(int k=0;k<8;k++)
						dfs(i,j,0,k);
				}
			}
		}
		for(int i=1;i<=n;i++) {
			for(int j=1;j<=n;j++) {
				if(vis[i][j])	System.out.print(ch[i][j]);
				else	System.out.print("*");
			}
			System.out.println();
		}
	}
}

【洛谷】P1219 八皇后

原题链接：https://www.luogu.com.cn/problem/P1219

• 思路：
  1. 经典的八皇后问题，深搜 + 回溯。我们从第一行到第 n 行地放皇后，所以其实第几个皇后就是第几行，那么我们只要遍历每一列即可。
  2. 用数组 ans[i] 表示第 i 个皇后占领了第几列，数组 a[i] 表示该列是否被占领，数组 b[i] 表示左下到右上的对角线是否被占领，数组 c[i] 表示左上到右下的对角线是否被占领。
  3. 难点在于对角线的表示，可以理解为 第 m 个皇后放在第 i 列，那么另一条对角线就是反过来 m + n - i 。同时用 total 记录方案数，小于等于 3 的就是前三个方案数，输出序列。

Code：

import java.util.Scanner;
public class Main {
	static int total=0,n;
	static int[] ans = new int[30];	//表示第 i 个皇后占领了第几列
	static boolean[] a = new boolean[30];	//表示该列是否被占领
	static boolean[] b = new boolean[30];	//表示左下到右上的对角线是否被占领
	static boolean[] c = new boolean[30];	//表示左上到右下的对角线是否被占领
	static void dfs(int m) {
		if(m>n) {
			total++;
			if(total<=3) {
				for(int i=1;i<=n;i++)
					System.out.print(ans[i]+" ");
				System.out.println();
			}
			return;	//返回上一层
		}
		for(int i=1;i<=n;i++) {	//搜索每一列
			if(!a[i] && !b[m+i] && !c[m+n-i]) {
				ans[m]=i;
				a[i]=true;
				b[m+i]=true;
				c[m+n-i]=true;
				dfs(m+1);
				a[i]=false;	//回溯
				b[m+i]=false;
				c[m+n-i]=false;
			}
		}
	}
	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		n = cin.nextInt();
		dfs(1);
		System.out.println(total);
	}
}

【HDU】2563 统计问题

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=2563

• 思路： 入门题，该题正解应该是用递推，但是 DFS 也可以，起始点定为（50，50），防止出现负数v。传入的参数就是变化的数，即方案数，起始为 0，以及起始点坐标。
  
  

Code：

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    static int ans=0,n;
    static int[][] dir = {{0,-1},{0,1},{-1,0}};
    static boolean[][] vis = new boolean[100][100];
    static void dfs(int m,int x,int y) {
        if(m==n) {
            ans++;
            return;
        }
        for(int i=0;i<3;i++) {
            int xx = x+dir[i][0];
            int yy = y+dir[i][1];
            if(!vis[xx][yy]) {
                vis[xx][yy]=true;
                dfs(m+1,xx,yy);
                vis[xx][yy]=false;
            }
        }
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int c = cin.nextInt();
        while(c-- >0) {
            for(int i=0;i<100;i++)
                for(int j=0;j<100;j++)
                    vis[i][j]=false;
            vis[50][50]=true;
            ans=0;
            n = cin.nextInt();
            dfs(0,50,50);
            System.out.println(ans);
        }
    }
}

【HDU】1035 Robot Motion

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1035

• 题意： 给出一个N*M地图，地图上表明了方向（N上S下W左E右），机器人从第一行第start列开始按照地图方向走：若能走出地图，输出直到走出地图所用的步数，后接 “step(s) to exit” ；若不能走出地图（走进了一个死循环），输出走进循环之前的步数a，以及循环的步数b，输出格式 “a step(s) before a loop of b step(s)” 。以 0 0 结束输入
• 思路： 用一个标记数组 vis[ ][ ] ，未走过的标记为 0 ，走过一遍的标记为 1 ，走过两遍标记为 2 ，用变量 ans1 表示走过的总步数，变量 ans2 表示循环的步数，也就是标记为 2 的方块数。如果超出了边界，则说明走出了迷宫。有点坑的是，一开始用 toCharArrays() 来输入二维字符数组导致一直 WA ，不知道为什么。

Code：

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    static int ans1,ans2,n,m,s;
    static char[][] maps = new char[50][50];
    static int[][] vis = new int[50][50];
    static void dfs(int x,int y) {
        if(x<0 || x>=n || y<0 || y>=m) {
            System.out.println(ans1 + " step(s) to exit");
            return;
        }
        if(vis[x][y]==1)    ans2++;
        if(vis[x][y]==2) {
            System.out.println(ans1-ans2*2 + " step(s) before a loop of " + ans2 + " step(s)");
            return;
        }
        ans1++;
        vis[x][y]++;
        if(maps[x][y]=='N')    dfs(x-1,y);
        if(maps[x][y]=='S') dfs(x+1,y);
        if(maps[x][y]=='E') dfs(x,y+1);
        if(maps[x][y]=='W') dfs(x,y-1);
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner cin = new Scanner(System.in);
        while(cin.hasNext()) {
            n = cin.nextInt();    m = cin.nextInt();    s = cin.nextInt();
            if(n==0 && m==0 && s==0)    break;
            for(int i=0;i<50;i++)
                for(int j=0;j<50;j++) {
                    vis[i][j]=0;
                    maps[i][j]='0';
                }    
            ans1=0;    ans2=0;
            for(int i=0;i<n;i++) {
                String str = cin.next();
                for(int j=0;j<m;j++)
                    maps[i][j] = str.charAt(j);
            }
            dfs(0,s-1);
        }
    }
}

【HDU】1045 Fire Net

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1045

• 题意： 有一个n*n城市（n<=4），地图已输入，”.”表示空地，可以安置武器，“#”表示墙，不可安置武器，武器也不可打穿它。武器只能直线射击。
  现在需要在城市布防，此城有如下规定：1. 两个武器不能在同一条直线上；2. 若两个武器直线之间有墙，则可以安置。求出此城最多可以安置的武器数量。
• 思路： 因为墙壁的两边可以一起放武器，所以就得全部搜索。输入参数是武器数量，从 0 开始搜索，搜索的过程不断更新。每次搜索就要判断同行同列是否有武器，遇到墙壁就跳出循环。可放置武器的话就标记并回溯。搜索题有多组输入的记得初始化。

Code：

import java.util.Scanner;
public class Main {
    static int ans,n;
    static char[][] maps = new char[10][10];
    static boolean[][] vis = new boolean[10][10];
    static boolean check1(int x,int y) {
        if(x<1 || x>n || y<1 || y>n)    return false;
        return true;
    }
    static boolean check2(int x,int y) {
        if(maps[x][y]=='X')    return false;
        for(int i=x;check1(i,y);i++) {
            if(maps[i][y]=='X')    break;
            if(vis[i][y])    return false;
        }
        for(int i=x;check1(i,y);i--) {
            if(maps[i][y]=='X')    break;
            if(vis[i][y])    return false;
        }
        for(int i=y;check1(x,i);i++) {
            if(maps[x][i]=='X')    break;
            if(vis[x][i])    return false;
        }
        for(int i=y;check1(x,i);i--) {
            if(maps[x][i]=='X')    break;
            if(vis[x][i])    return false;
        }
        return true;
    }
    static void dfs(int m) {
        ans=Math.max(ans, m);
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=n;j++) {
                if(check2(i,j)) {
                    vis[i][j]=true;
                    dfs(m+1);
                    vis[i][j]=false;
                }
            }
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub、
        Scanner cin = new Scanner(System.in);
        while(cin.hasNext()) {
            ans=0;
            n = cin.nextInt();
            if(n==0)    break;
            for(int i=0;i<=8;i++)
                for(int j=0;j<=8;j++) {
                    vis[i][j]=false;
                    maps[i][j]='0';
                }
            for(int i=1;i<=n;i++) {
                String str = cin.next();
                for(int j=1;j<=n;j++) 
                    maps[i][j] = str.charAt(j-1);
            }
            dfs(0);
            System.out.println(ans);
        }
    }
}

【HDU】1010 Tempter of the Bone (奇偶剪枝)

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1010

• 题意： 小狗能否从起点S，经过时间T，恰好到达终点D。‘.’表示可以走的路，’#’表示不能走的墙，’S’表示开始位置，‘D’表示结束位置，不能走回头路。

• 思路： 奇偶剪枝的典型题。没有剪枝就会 TLE。设当前位置 (x, y) 到 D 点 (dx, dy) 的最短距离为 minn，到达当前位置 (x, y)已经花费时间 (步数) sum，题目要求的时间T。

  1. 奇偶剪枝：对于当前位置 (x, y)，如果 T - sum 与 minn 的奇偶性不同，则剪掉。
  2. 可达性剪枝：如果 T - sum < minn，则剪掉。
  3. 可达性剪枝：如果一开始给定时间与最短路径差值不是偶数或者比最短路径小就可以直接输出 “NO” 了。

不懂奇偶剪枝的看这里：【总结】DFS常用技巧详解 —— 奇偶剪枝

Code：

import java.util.Scanner;
public class Main {
	static int n,m,t,sx,sy,ex,ey;
	static boolean flag;
	static int[][] dir = {{1,0},{-1,0},{0,1},{0,-1}};
	static boolean[][] vis = new boolean[10][10];
	static char[][] maps = new char[10][10];
	static void dfs(int x,int y,int sum) {
		if(flag)	return;		//巨坑，没这句就会TLE
		if(maps[x][y]=='D' && sum==t) {
			flag=true;
			return;
		}
		if((t-sum)%2!=(Math.abs(x-ex)+Math.abs(y-ey))%2)	return;		//奇偶剪枝
		if(t-sum<Math.abs(x-ex)+Math.abs(y-ey))	return;	//可达性剪枝
		for(int i=0;i<4;i++) {
			int xx=x+dir[i][0];
			int yy=y+dir[i][1];
			if(xx>=1 && xx<=n && yy>=1 && yy<=m && !vis[xx][yy] && maps[xx][yy]!='X') {
				vis[xx][yy]=true;
				dfs(xx,yy,sum+1);
				vis[xx][yy]=false;
			}
		}
		return;
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner cin = new Scanner(System.in);
		while(cin.hasNext()) {
			flag=false;
			for(int i=0;i<=8;i++)
				for(int j=0;j<=8;j++) {
					vis[i][j]=false;
					maps[i][j]='0';
				}
			n = cin.nextInt();	m = cin.nextInt();	t = cin.nextInt();
			if(n==0 && m==0 && t==0)	break;
			for(int i=1;i<=n;i++) {
				String str = cin.next();
				for(int j=1;j<=m;j++) {
					maps[i][j] = str.charAt(j-1);
					if(maps[i][j]=='S') {
						sx=i;
						sy=j;
					}
					if(maps[i][j]=='D') {
						ex=i;
						ey=j;
					}
				}
			}
			int minn = (Math.abs(sx-ex)+Math.abs(sy-ey));
			if((t-minn)%2==1 || t<minn) {	//奇偶剪枝
				System.out.println("NO");
				continue;
			}
			vis[sx][sy]=true;
			dfs(sx,sy,0);
			if(flag)	System.out.println("YES");
			else	System.out.println("NO");
		}
	}
}

【HDU】1015 Safecracker

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1015

• 题意： 有一个数字n和一个字符串，请你从字符串中选出五个字母，字母的大小按照字母表的顺序，比如(A=1, B=2, …, Z=26)。假设依次选出的字母为v、w、x、y、z 使其满足以下式子$$v-w^2+x^3-y^4+z^5=n$$比如：给出一个n = 1 和字符串 ABCDEFGHIJKL，一个可能的结果为FIECB$$6-9^2+5^3-3^4+2^5=1$$请输出满足条件字典序最大的字符串，以 ”0 END” 结束

• 思路： 为了使字典序最大，那么字符串先从大到小排序，找到了即为字典序最大。将字符串转换为数字存入数组。以搜索到的字符数量为变量进行搜索，从 0 开始，搜索的过程中存入数组 ans ，当搜索到 5 时也就是已经搜到了 5 个字符了，就判断是否符合条件，标记。最后再转换为字符输出。

Code：

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

class node{    //定义结构体
    int x, y;
    public node(int x, int y) {
        this.x=x;
        this.y=y;
    }
    public int compare(node a) {    //结构体从小到大排序
        return this.x-a.x;
    }
}
public class Main {
    static int n;
    static String str;
    static boolean flag;
    static Integer[] a = new Integer[20];	//为了排序，定义为Integer类型
    static int[] ans = new int[20];
    static boolean[] vis = new boolean[20];
    static Comparator<Integer> cmp = new Comparator<Integer>() {	//从小到大排序
        public int compare(Integer a, Integer b) {
            return b-a;
        }
    };
    static void dfs(int dept) {
        if(flag)    return;
        if(dept==5) {
            if(ans[0]-Math.pow(ans[1], 2)+Math.pow(ans[2], 3)-Math.pow(ans[3], 4)+Math.pow(ans[4], 5)==n)
                flag=true;
            return;
        }
        for(int i=0;i<str.length();i++) {
            if(!vis[i] && !flag) {
                vis[i]=true;
                ans[dept]=a[i];
                dfs(dept+1);
                vis[i]=false;
            }
        }
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        while(cin.hasNext()) {
            flag=false;
            Arrays.fill(vis, false);	//只能初始化一维数组
            n = cin.nextInt();    str = cin.next();
            if(n==0 && str.equals("END"))    break;
            for(int i=0;i<str.length();i++)
                a[i]=str.charAt(i)-'A'+1;
            Arrays.sort(a,0,str.length(),cmp);
            dfs(0);
            if(flag) {
                for(int i=0;i<5;i++)
                    System.out.print((char)(ans[i]-1+'A'));
                System.out.println();
            }
            else    System.out.println("no solution");
        }
    }
}

【HDU】1016 Prime Ring Problem

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1016

• 题意： 已知一个数 n，要求将数字 1~n 围成一个圆环，使得相邻两个数之和为素数。
• 思路： 先将一定范围内是否为素数的结果存入数组，然后 第一个位置永远为 1，从 2 ~ n 开始深搜，判断是否符合条件，当找到最后一个数 n+1，就判断第一个数以及最后一个数之和是否为素数。

Code：

import java.util.Scanner;
public class Main {
    static int n;
    static int[] ans = new int[50];
    static boolean[] prime = new boolean[50];
    static boolean[] vis = new boolean[50];
    static void isPrime() {		//埃氏筛法
        for(int i=0;i<50;i++)
            prime[i]=true;
        prime[0]=prime[1]=false;
        for(int i=2;i<50;i++) {
            if(prime[i])
                for(int j=i+i;j<50;j+=i)
                    prime[j]=false;
        }
    }
    static void dfs(int x) {
        if(x==n+1 && prime[ans[1]+ans[x-1]]) {	//最后一个点
            for(int i=1;i<=n;i++)
                if(i!=n)    System.out.print(ans[i]+" ");
                else    System.out.println(ans[i]);
            return;
        }
        for(int i=2;i<=n;i++) {
        //没有用过且该数与上一个数之和为素数
            if(!vis[i] && prime[i+ans[x-1]]) {	
                vis[i]=true;
                ans[x]=i;
                dfs(x+1);
                vis[i]=false;	//回溯
            }
        }
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int t=0;
        isPrime();
        while(cin.hasNext()) {
            for(int i=0;i<=25;i++)
                vis[i]=false;
            n = cin.nextInt();
            ans[1]=1;	//1始终在第一个位置
            System.out.println("Case " + ++t + ":");
            dfs(2);
            System.out.println();
        }
    }
}

【HDU】1258 Sum It Up (去重技巧)

原题链接：http://acm.hdu.edu.cn/showproblem.php?pid=1258

• 题意： 给一个数 t ，再给一个数 n 表示数组大小，接下来给出数组的 n 个数，求由此数组中任意个数组成非递增的排列，其和等于 t ，没有的输出 “NONE” 。
• 思路： 搜索 + 去重技巧。如果只是简单搜索的话，结果会输出重复的排列以及不是非递增排列，因为给的数组里的数可以重复。所以在搜索的过程中，要去重，当找到了要判断是否为非递增排列。

Code：

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;
public class Main {
	static int t,n;
	static boolean flag;
	static Integer[] a = new Integer[20];
	static int[] ans = new int[20];
	static boolean[] vis = new boolean[20];
	static Comparator<Integer> cmp = new Comparator<Integer>() {
		public int compare(Integer a, Integer b) {
			return b-a;
		}
	};
	static void dfs(int m,int sum) {
		if(sum==t) {
			for(int i=0;i<m-1;i++) {	//非递减序列剪掉
				if(ans[i]<ans[i+1])
					return;
			}
			flag=true;
			for(int i=0;i<m;i++) {
				if(i==m-1)	System.out.println(ans[i]);
				else	System.out.print(ans[i]+"+");
			}
			return;
		}
		if(sum>t)	return;	//总数超的剪掉
		if(m>n)	return;	//超过数组大小的剪掉
		for(int i=1;i<=n;i++) {
			if(!vis[i]) {
				vis[i]=true;
				ans[m]=a[i];
				dfs(m+1,sum+a[i]);
				vis[i]=false;
				while(i+1<=n && a[i]==a[i+1])	i++;	//去重
			}
		}
	}
	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		while(cin.hasNext()) {
			t = cin.nextInt();	n = cin.nextInt();
			if(t==0 && n==0)	break;
			flag=false;
			Arrays.fill(vis, false);
			System.out.println("Sums of " + t + ":");
			for(int i=1;i<=n;i++)
				a[i]=cin.nextInt();
			Arrays.sort(a,1,n+1,cmp);
			dfs(0,0);
			if(!flag)	System.out.println("NONE");
		}
	}
}

【POJ】2676 Sudoku (数独问题)

原题链接：http://poj.org/problem?id=2676

题意： 九宫格问题，也叫数独问题。把一个9行9列的网格，再细分为9个3*3的子网格，要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字，即每行、每列、每个子网格内都不允许出现相同的数字。0是待填位置，其他均为已填入的数字。要求填完九宫格并输出（如果有多种结果，则只需输出其中一种）。如果给定的九宫格无法按要求填出来，则输出原来所输入的未填的九宫格

思路：

用三个数组进行标记每行、每列、每个子网格已用的数字。

row[i][x] 标记在第i行中数字x是否出现了

col[j][y] 标记在第j列中数字y是否出现了

grid[k][x] 标记在第 k 个 3*3 子格中数字 z 是否出现了

那么问题的难点就在于找出 grid 子网格的序号与 行 i 列 j 的关系，即要知道第 i 行 j 列的数字是属于哪个子网格的

首先我们假设子网格的序号如下编排：

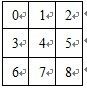
由于1<=i、j<=9，我们有：

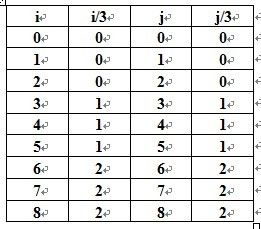
令a= i/3 , b= j/3 ，根据九宫格的 行列 与 子网格 的 关系，我们有:

不难发现 $$3a+b=k$$

即 $$3(i/3)+j/3=k$$
又我在程序中使用的数组下标为 1 ~ 9，grid 编号也为1 ~ 9

因此上面的关系式可变形为 $$3((i-1)/3)+(j-1)/3+1=k$$
有了这个推导的关系式，问题的处理就变得非常简单了，直接DFS即可。

思路参考大佬的：POJ2676-Sudoku

Code：

import java.util.Scanner;
public class Main {
	static int t,sum;
	static boolean flag;
	static int[][] maps = new int[20][20];
	static boolean[][] row = new boolean[20][20];
	static boolean[][] col = new boolean[20][20];
	static boolean[][] grid = new boolean[20][20];
	static void dfs(int x,int y) {
		if(flag)	return;
		if(maps[x][y]!=0) {
			if(x==9 && y==9) {
				for(int i=1;i<=9;i++) {
					for(int j=1;j<=9;j++)
						System.out.print(maps[i][j]);
					System.out.println();
				}
				flag=true;
				return;
			}
			if(y==9) dfs(x+1,1);
			else	dfs(x,y+1);
		}else {
			int k = 3*((x-1)/3)+(y-1)/3+1;
			for(int i=1;i<=9;i++) {
				if(!row[x][i] && !col[y][i] && !grid[k][i]) {
					maps[x][y]=i;
					row[x][i]=true;
					col[y][i]=true;
					grid[k][i]=true;
					if(x==9 && y==9) {
						for(int p=1;p<=9;p++) {
							for(int q=1;q<=9;q++)
								System.out.print(maps[p][q]);
							System.out.println();
						}
						flag=true;
						return;
					}
					if(y==9)	dfs(x+1,1);
					else	dfs(x,y+1);
					maps[x][y]=0;
					row[x][i]=false;
					col[y][i]=false;
					grid[k][i]=false;
				}
			}
		}
	}
	public static void main(String[] args) {
		Scanner cin = new Scanner(System.in);
		t = cin.nextInt();
		while(t-- >0) {
			flag=false;
			for(int i=0;i<15;i++) {
				for(int j=0;j<15;j++) {
					row[i][j]=false;
					col[i][j]=false;
					grid[i][j]=false;
				}
			}
			for(int i=1;i<=9;i++) {
				String str = cin.next();
				for(int j=1;j<=9;j++) {
					maps[i][j] = str.charAt(j-1)-'0';
					if(maps[i][j]!=0) {
						int k = 3*((i-1)/3)+(j-1)/3+1;
						row[i][maps[i][j]]=true;
						col[j][maps[i][j]]=true;
						grid[k][maps[i][j]]=true;
					}
				}
			}
			dfs(1,1);
		}
	}
}