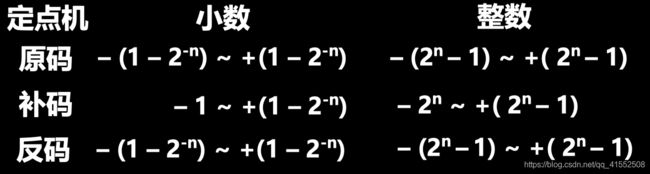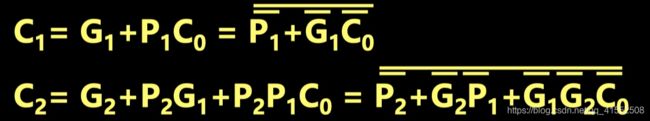计算机组成原理完整学习笔记（五）：计算方法

前言

如果你对这篇文章可感兴趣，可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」，查看完整博客分类与对应链接。

第五章 计算方法

5.1 机器数表示方法

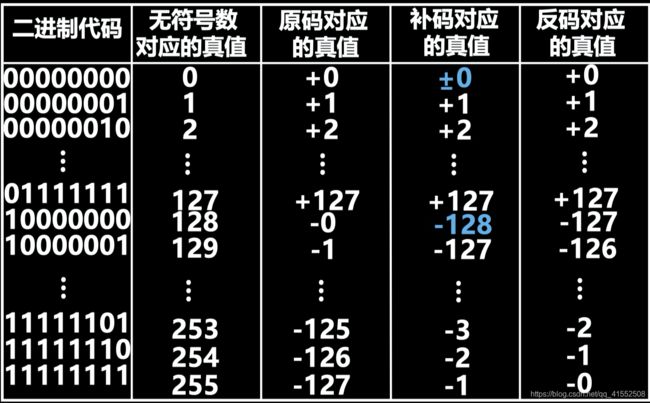
5.1.1 数的原码表示

概念

符号位为 0 表示正数，为 1 表示负数，数值部分为真值的绝对值，又称为带符号的绝对值。

书写

约定书写时，正数的符号位与数值位用逗号分隔，小数的符号位与数值位用小数点分隔。

原码整数定义

$$[x{]}_{原}=\{\begin{array}{rl}0,x& 2^n>x\ge 0\\ 2^n-x& 0\ge x>-2^n\end{array}$$

原码小数定义

$$[x{]}_{原}=\{\begin{array}{rl}x& 1>x\ge 0\\ 1-x& 0\ge x>-1\end{array}$$

举例：求 x=0 的原码

若 x 为小数，则
$$\begin{gathered} [+0.0000{]}_{原}=0.0000 \\ [-0.0000{]}_{原}=1.0000-0.0000=1.0000 \end{gathered}$$

若 x 为整数，则
$$\begin{gathered} [+0{]}_{原}=0,0000 \\ [-0{]}_{原}=1,0000 \end{gathered}$$

特点

优点：表示方法简单，直观

缺点：加减运算复杂

5.1.2 数的补码表示

引入

减去一个数，可以用加上这个数的补数来代替，从而可以把减法转变为加法。

• 一个负数可用其正的补数来代替，这个正补数可以用此负数加模来求得。
• 一个正数和负数互为补数时，他们的绝对值之和即为模数。
• 正数的补数即为该正数本身。
• （负数的补码）符号位不变，数值位从左到右依次取反，最右边的 1 及其后的 0 不变。

补码整数定义

$$[x{]}_{补}=\{\begin{array}{rl}0,x& 2^n>x\ge 0\\ 2^{n+1}+x& 0>x\ge -2^n(mod{2}^{n+1})\end{array}$$

$$\begin{gathered} [-1011000{]}_{补}=2^{7+1}+(-1011000)=1,0101000 \\ [+1010{]}_{补}=0,1010 \end{gathered}$$

补码小数定义

$$[x{]}_{补}=\{\begin{array}{rl}x& 1>x\ge 0\\ 2+x& 0>x\ge -1(mod2)\end{array}$$

$$\begin{gathered} [+0.1110{]}_{补}=0.1110 \\ [-0.1100000{]}_{补}=2+(-0.1100000)=1.0100000 \end{gathered}$$

举例

5.1.3 数的移码表示

引入

补码表示很难直接判断其真值大小，因此对所有补码都加上一个 $2^n$，得到了移码，可以直观地比较数值大小。

因此用移码表示浮点数的阶码可以方便地判断浮点数的阶码大小。

定义

$$[x{]}_{移}=2^n+x(2^n>x\ge -2^n)$$

移码与补码的数值部分相同，符号位相反。

5.1.4 各机器数表示总结

5.2 定点数与浮点数

5.2.1 定点数

定义

定点数即小数点位置固定的数。

5.2.2 浮点数

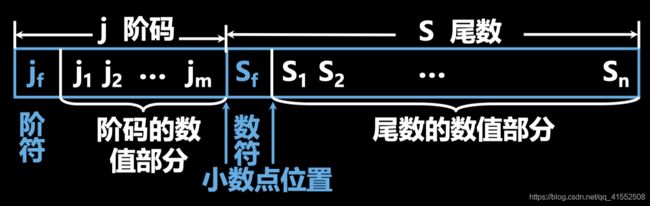
浮点数一般形式

$$N=S\ast r^j$$

S为尾数，j为阶码，r为基数（可取2、4、8、16等）

$$\begin{array}{rl}N& =11.0101\\ & =0.110101\ast 2^{10}\end{array}$$

小数位第 1 位为 1，且整数部分为 0，为规格化数。

浮点数在机器中的表示形式

$S_f:$ 代表浮点数的符号
$n:$ 其位数反映浮点数的精度
$m:$ 其位数反映浮点数的表示范围
$j_f,m:$ 共同表示小数点的实际位置

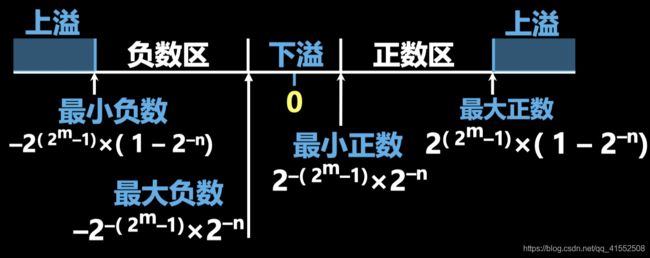
浮点数的表示范围

上溢: 阶码 > 最大阶码 中断溢出处理

下溢: 阶码 < 最小阶码 按机器零处理

浮点数的规格化表示

1. r=2，尾数的最高位为 1
2. r=4，尾数的最高 2 位不全为 0
3. r=8，尾数的最高 3 位不全为 0

5.3 定点数移位和加减法运算

5.3.1 定点数移位运算

算术移位（有符号数移位）规则

符号位不变，数值位如下变化。

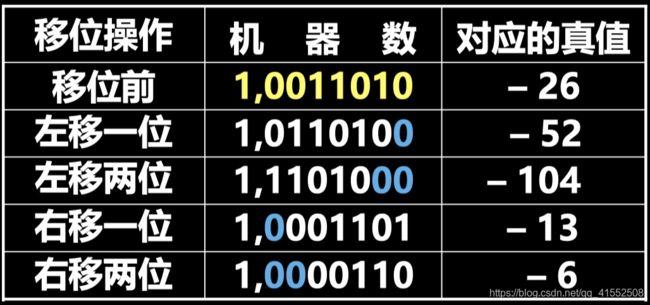
正数移位举例

$$\begin{gathered} A=+26=+11010 \\ [A{]}_{原}=[A{]}_{补}=[A{]}_{反}=0,0011010 \end{gathered}$$

负数原码移位举例

$$\begin{gathered} A=-26=-11010 \\ [A{]}_{原}=1,0011010 \end{gathered}$$

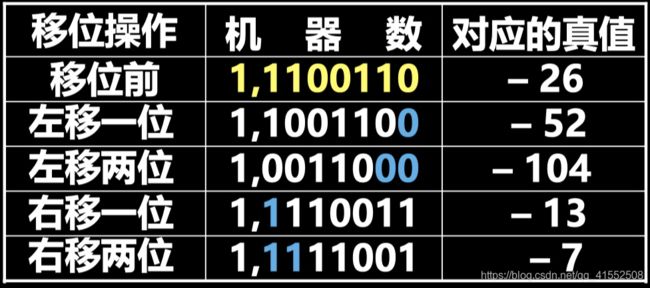
负数反码移位举例

$$\begin{gathered} A=-26=-11010 \\ [A{]}_{反}=1,1100101 \end{gathered}$$

负数补码移位举例

$$\begin{gathered} A=-26=-11010 \\ [A{]}_{补}=1,1100110 \end{gathered}$$

移位总结

定点数移位，符号位不变。左移时，高位丢有效位，结果出错；右移时，低位丢有效位，影响精度。

原码: 高位有效位 - 1，低位有效位 - 1
反码: 高位有效位 - 0，低位有效位 - 0
补码: 高位有效位 - 0，低位有效位 - 1

算术移位和逻辑移位

1. 算术移位: 有符号数的移位
2. 逻辑移位: 无符号数的移位
   • 逻辑左移: 低位补 0，高位移丢
   • 逻辑右移: 高位补 0，低位移丢

5.3.2 定点数加减法及溢出判断

定点数加减法

连同符号位一起相加，符号位产生的进位自然丢掉。

溢出

运算结果超出计算机字长所能表示范围的情况，称为溢出。

下述两个例子中的补码运算均发生了溢出。

溢出判断1 —— 符号相同两数相加减

参加运算的两个数（补码形式）符号相同，若其结果的符号与原操作数的符号不同，则发生了溢出。

两数符号位相同，结果的符号位发生变化，溢出。

溢出判断2 —— 最高位进位与符号位

参加运算的两个数，符号位可以不同，如果运算结果中最高数值位的进位与符号位的进位不同，则发生了溢出。

最高数值位无进位，符号位有进位，溢出。

溢出判断3 —— 两位符号位

参加运算的两个数，均采用双符号位（变形补码），如果结果的两位符号位不同，则发生了溢出。

输出结果两位符号位不同，溢出。

无论是否发生溢出，双符号位的高位总代表真正的符号，如果该位为 1，表示结果为负，此时称为下溢，如果该位为 0，表示结果为正，此时称为上溢。

5.4 定点数乘除法运算

5.4.1 定点数乘法运算

定点数乘法分类

1. 定点数一位乘法
   • 定点原码一位乘法
   • 定点补码一位乘法
     • 校正法
     • 布斯法（booth）
2. 定点数二位乘法
   • 定点原码两位乘
   • 定点补码两位乘

定点原码一位乘性质

1. 右移代替左移。部分积相加时最低位只用一次，此位将来不再参与运算，因此可将部分积寄存器右移一位。
2. 乘数的各个位从右向左均只用一次，最低位不再使用，因此部分积右移时，乘数寄存器也可右移一位，即可用乘数寄存器的最高位接收部分积移出的位。

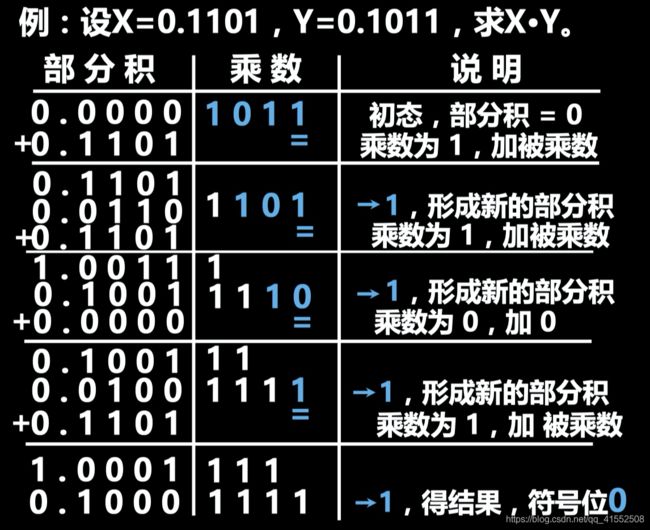
定点原码一位乘举例

1. 乘积的符号位 $x_{0}xor{y}_0=0xor0=0$
2. 数值部分按绝对值相乘

定点原码一位乘特点

1. 用移位的次数判断乘法是否结束
2. 绝对值运算
3. 逻辑移位

5.4.2 定点数除法运算

定点数除法分类

1. 定点原码一位除
   • 恢复余数法
   • 加减交替法
2. 定点补码一位除

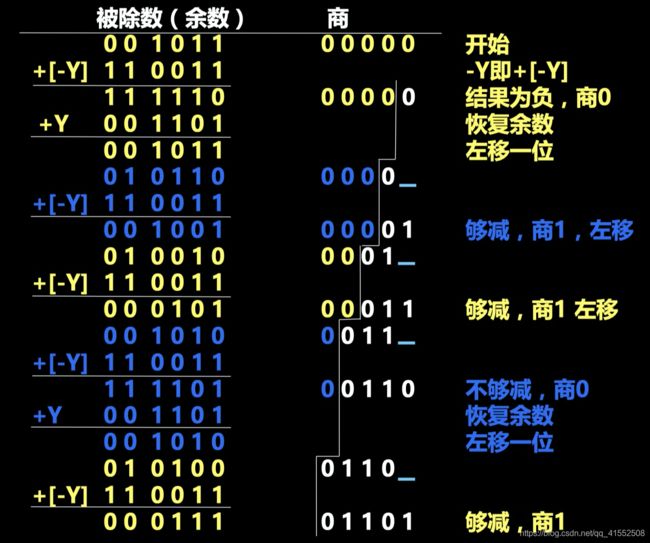
恢复余数法

特点:

1. 左移被除数（余数）来代替右移除数。
2. 速度慢，控制方式复杂。

上商规则:

1. 将部分余数 $R_i$ 与除数 $Y$ 相减，判断余数的符号，确定商的值。
2. 差为正: 商上 1，不恢复余数，部分余数左移 1 位。
3. 差为负: 商上 0，恢复余数，部分余数左移 1 位。

例题

$X=0.1011，Y=0.1101，求X/Y$

采用双符号位进行计算，高位符号位代表了实际极性，所以可以防止因溢出而丢掉正确的符号。

最终结果: $X/Y=0.1101$，符号为正，余数为 $0.0111\ast 2^{-4}$。

$2^{-4}$ 是因为计算过程中左移了 $4$ 次。

总结

1. 运算过程中，被除数寄存器不断左移，右侧补零
2. 商的初值为0，不断左移
3. 可以认为是将商的高位移入零被除数寄存器的低位部分。
4. 所以初始时可以用存放商的寄存器存放被除数的低 n 位，实现 2n 位数除以 n 位数。

5.5 浮点数运算

5.5.1 浮点加减运算步骤

$$\begin{gathered} x=S_x\ast 2^{j_x} \\ y=S_y\ast 2^{j_y} \end{gathered}$$

五个步骤: 对阶、尾数相加减、规格化、舍入、判溢出

5.5.2 对阶

操作目的: 使两数阶码一致，尾数加减可以进行

• 比较两阶码，$\Delta J=J_x-J_y$
• 将小阶码数的尾数右移 $|\Delta J|$ 位，其阶码值加 $|\Delta J|$
• 注意尾数右移特点: 原码补0，补码补符号位
• 右移过程中移掉的位可用附加位电路暂时保存

5.5.3 尾数加/减运算

$$\Delta S=S_x\pm S_y$$

采用双符号位加减运算。

5.5.4 尾数规格化

操作目的: 尽可能提高精度

$$\begin{gathered} 2^{-1}\le |[S{]}_{原}|\le 1-2^{-n} \\ {2}^{-1}\le |[S{]}_{补}|\le 1 \end{gathered}$$

右规

结果的两个符号位不同表示尾数结果溢出，右移 1 位尾数，阶码 $J+1$。

左规

结果的两个符号位相同，如是原码且数值位最高位为 0，则左移；如是补码且数值位与符号位相同也需左移。同时阶码减去移动的位数。

5.5.5 舍入

截断法

直接丢掉附加位电路中的数据。

恒置 1 法

类似于上取整，把计算结果最后一位置 1。

0舍1入法

类似于四舍五入，如果附加位电路中最高位为1，则对数值进 1。

5.5.6 判断阶码溢出

• 阶码下溢，则置运算结果为机器零
• 阶码上溢，则置溢出标志，报警中断

5.5.7 例题

$$X=2^{0010}\ast (0.11011011),Y=2^{0100}\ast (-0.10101100)，求X+Y$$

• 对阶操作

$$\begin{gathered} \Delta J=[J_x{]}_{补}+[-J_y{]}_{补}=11110 \\ [S_x{]}_{补}=00.0011011011,J=00100 \end{gathered}$$

• 尾数相加

$$[S_x{]}_{补}+[S_y{]}_{补}=00.001101101111+11.01010100=11.1000101011$$

• 规格化操作

符号位相同，左规，移 1 位，$ans=11.0001010110,J=00011$。

• 舍入

采用 0 舍 1 入法，得到 $[S{]}_{补}=11.00010110,S=-0.11101010$。

• 判溢出

未溢出，最终结果为 $X+Y=2^{0011}\ast (-0.11101010)$。

5.6 加法器与算术逻辑单元

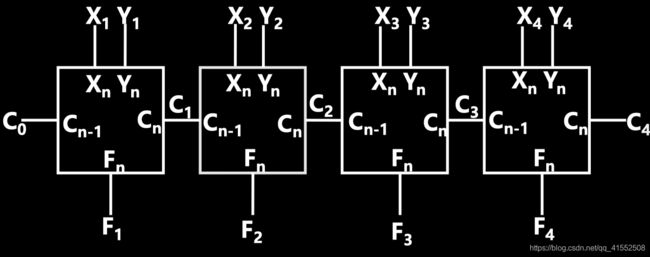
5.6.1 n 位串行加法器

$$\begin{gathered} C_1=X_1{Y}_1+(X_1+Y_1)C_0 \\ {C}_2=X_2{Y}_2+(X_2+Y_2)X_1{Y}_1+(X_2+Y_2)(X_1+Y_1)C_0 \\ ... \end{gathered}$$

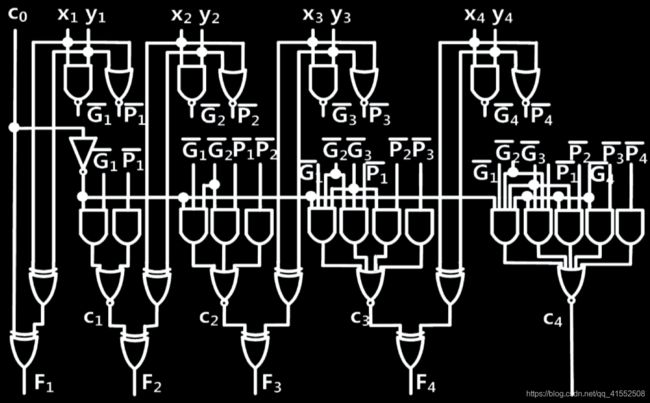
5.6.2 超前进位加法器

令 $P_i=X_i+Y_i,G_i=X_i{Y}_i$，则
$$\begin{gathered} C_1=G_1+P_1{C}_0 \\ {C}_2=G_2+P_2{G}_1+P_2{P}_1{C}_0 \end{gathered}$$

因此可以改进串行加法器，使得加法运算速度与运算数字长度无关。