蚁群优化算法（讨论参数对算法收敛的作用）

1.蚁群优化算法理解

蚁群优化（ant colonyoptimization, ACO）是20世纪90年代初由意大利学者M.Dorigo等通过模拟蚂蚁的行为而提出的一种随机优化技术。
蚁群优化算法是仿照大自然蚂蚁觅食的行为寻找最优解的一种算法，在寻找食物的过程中，蚂蚁们会朝着不同的路径走，一边走一边留下气味信息给后来的同伴，距离食物最近的一条路走的蚂蚁会越来越多，气味也会越来越浓，而路程较远的路因为走的蚂蚁越来越少，气味也会慢慢挥发掉变淡，最终所有蚂蚁都走在；离食物最短的一条路上，从而达到寻求最短路径的目的。
蚁群优化算法也正是应用了这个过程，以求：从出发地不重复的经过n个城市回到出发地，路径最短的问题（TSP问题）为例。

2.算法基本流程

1、路径构建：
每只蚂蚁选择一个城市作为出发城市，维护一个路径记忆向量来存放该蚂蚁经过的城市，按随机比例规则选择下一个要到达的城市。
设蚂蚁k当前所在的城市为i，选择城市j作为下一个访问对象的概率为：

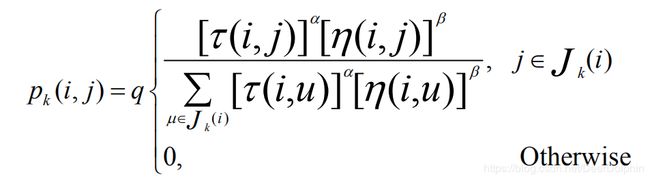
2、信息素更新：
每一轮过后，问题空间中所有路径上的信息素都会政法，我们为所有边上的信息素呈上一个小于1的常数，随后所有蚂蚁根据自己构建的路径长度在他们本轮经过的边上释放信息素。蚂蚁构建的路径越短、释放的信息素就越多：

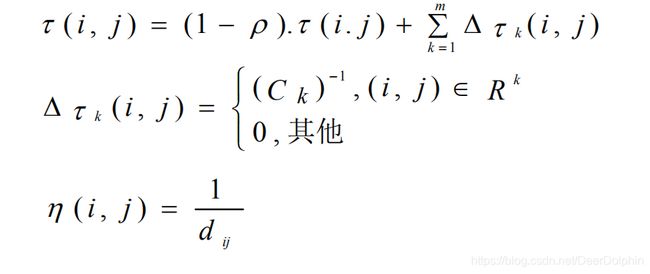
m是蚂蚁个数。p是信息的蒸发率（AS中通常设为0.5）,Ck表示路径长度。
3.AS求解TSP的流程图

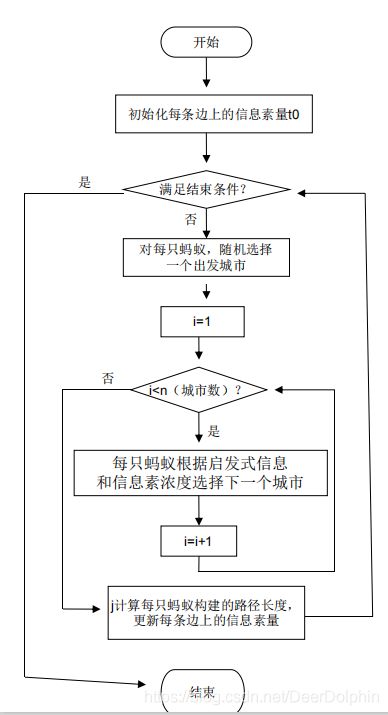
3.MATLAB代码实现

%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc

%% 导入数据
%load citys_data.mat
load city_1.mat%使用rand函数随机生成50*2个数据

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
%n = size(citys,1);
n = size(city,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2));%D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 40;                              % 蚂蚁数量50
alpha = 0.7;                           % 信息素重要程度因子1
beta = 5;                            % 启发函数重要程度因子5
rho = 0.6;                           % 信息素挥发因子0.1
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 100;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

%% 迭代寻找最佳路径
figure;
while iter <= iter_max
    fprintf('迭代第%d次\n',iter);
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表

 %   figure;
 %最佳路径的迭代变化过程
    [Shortest_Length,index] = min(Length_best(1:iter));
    Shortest_Route = Route_best(index,:);
    plot([city(Shortest_Route,1);city(Shortest_Route(1),1)],...%plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
    [city(Shortest_Route,2);city(Shortest_Route(1),2)],'o-');%[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
    pause(0.3);
 
    iter = iter + 1;
    Table = zeros(m,n);

 % end
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
plot([city(Shortest_Route,1);city(Shortest_Route(1),1)],...
     [city(Shortest_Route,2);city(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(city,1)
    text(city(i,1),city(i,2),['   ' num2str(i)]);
end
text(city(Shortest_Route(1),1),city(Shortest_Route(1),2),'       起点');
text(city(Shortest_Route(end),1),city(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

4.结果分析

通过更改m蚂蚁数量，alpha 启发信息素，beta信息浓度，rho 信息素挥发因子 这几个参数，发现每个参数的不同取值对算法最终结果的影响。

1.蚂蚁的数量

蚂蚁数目过多时，会使大量曾被搜索过的路径上的信息素的变化趋于平均,随机性加强,但收敛速度变慢;
蚂蚁数目过少时,可能会让那些从未被搜索到的路径上的信息量减少至0,随机性减弱,收敛速度变快,但是算法稳定性变差,得到的效果不佳。
数量过多：

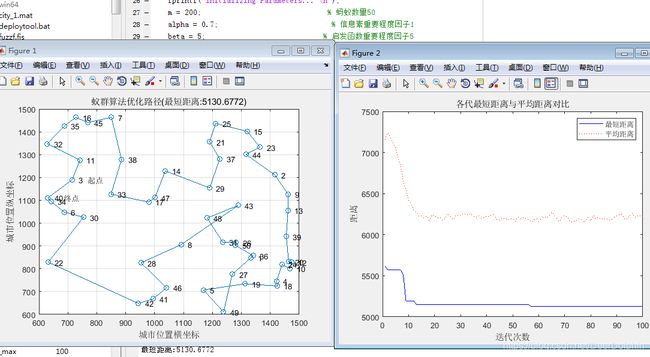
数量过少：

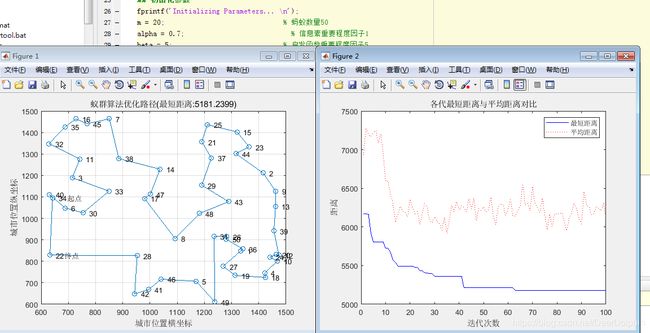
2.启发信息素

启发信息素舍得值过小时，蚂蚁选择以前走过的路径可能性会越大，收敛速度会变慢，且容易出现局部最优解，而取值过大时，会出现过早收敛的情况，达不到更好的效果。
数量过多：

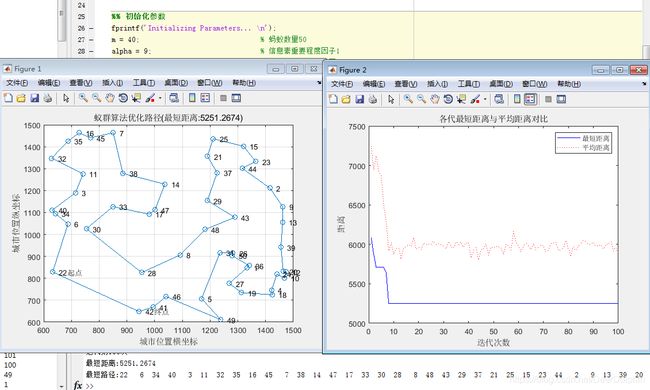
数量过少：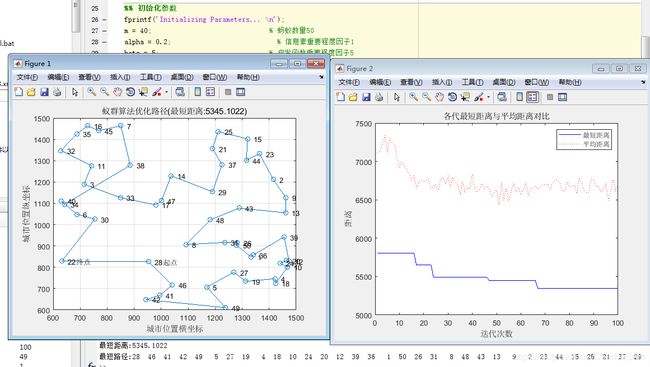

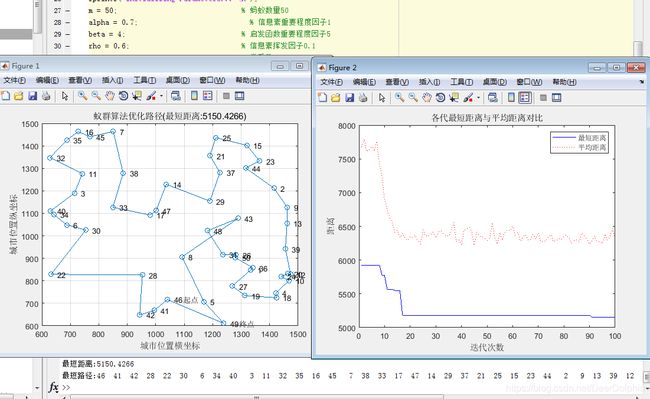
3.信息浓度

信息浓度过小，蚂蚁在选择路径上就基本近似于随机显示选择，对选取最短路径帮助不大，过大时收敛性能变差。
数量过多：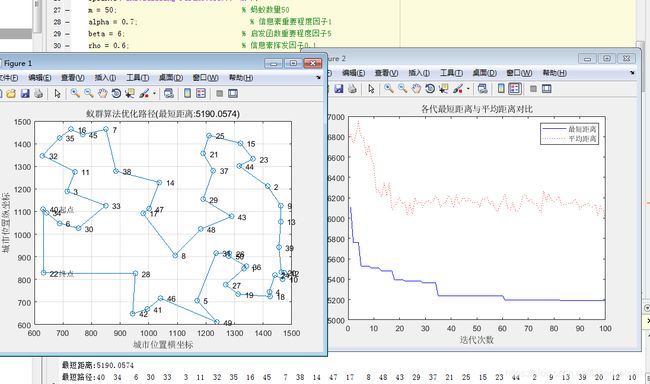
数量过少：

4.信息挥发因子

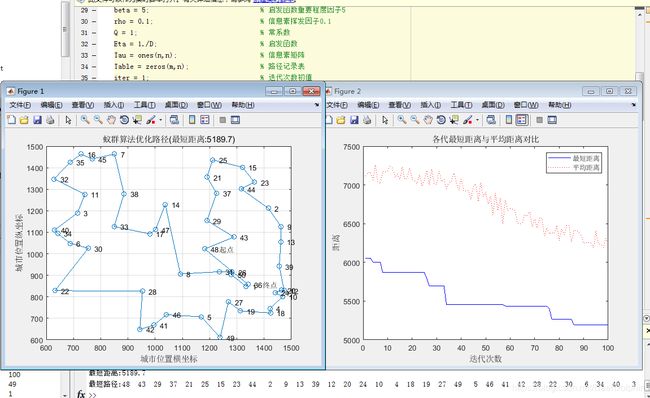
挥发因子过大时，部分路径被选中的可能性就更快的降低，收敛性提高，过小时，收敛性会降低。
数量过多：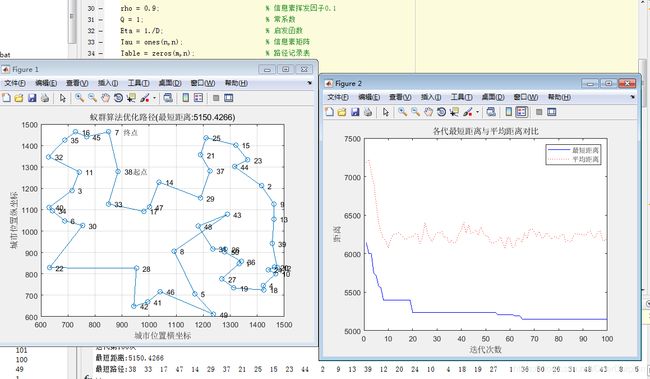
数量过少：

经过多次更改参数，这几个参数最优的取值是：
m = 40; % 蚂蚁数量
alpha = 0.7; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.6; % 信息素挥发因子

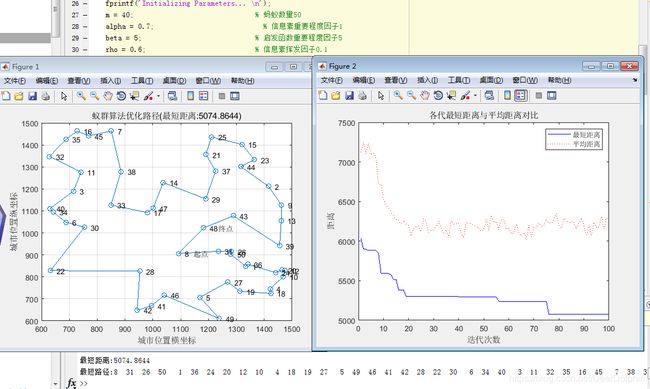
最短距离为：5076.8644