学习笔记(二):预测房价模型
问题描述
现有47个房子的面积和价格,请建立一个模型对新的房价进行预测。
分析
- 输入数据为房子的面积,一维。
- 目标数据为房子的房价,也是一维。
- 那么显然这属于监督学习中的线性回归(Regression)问题,可以使用多项式函数和平方误差函数来建立模型。
步骤
获取与处理数据
2104,399900
1600,329900
2400,369000
1416,232000
3000,539900
1985,299900
1534,314900
1427,198999
1380,212000
1494,242500
1940,239999
2000,347000
1890,329999
4478,699900
1268,259900
2300,449900
1320,299900
1236,199900
2609,499998
3031,599000
1767,252900
1888,255000
1604,242900
1962,259900
3890,573900
1100,249900
1458,464500
2526,469000
2200,475000
2637,299900
1839,349900
1000,169900
2040,314900
3137,579900
1811,285900
1437,249900
1239,229900
2132,345000
4215,549000
2162,287000
1664,368500
2238,329900
2567,314000
1200,299000
852,179900
1852,299900
1203,239500
因为数据的数字都很大,为了消除奇异样本数据导致的不良影响,我们要将输入数据标准化,即将横坐标X的范围限制在一定区间内,降低问题的复杂度。采用的公式如下:
X = X − X ‾ s t d ( X ) \begin{aligned} X=\frac{X-\overline{X}}{std(X)} \end{aligned} X=std(X)X−X
其中std(X)表示X的标准差,代码实现如下:
# 导入要用到的库
import numpy as np
import matplotlib.pyplot as plt
# 定义存储输入数据(x)和目标数据(y)的数组
x, y = [], []
# 遍历数据集,变量sample对于每个样本
for sample in open("./_Data/prices.txt","r"):
# 因为数据使用逗号隔开的,所以调用split方法
_x,_y = sample.split(",")
#将字符串转化为浮点数
x.append(float(_x))
y.append(float(_y))
# 读取数据后,将它们转化为Numpy数组
x, y = np.array(x), np.array(y)
# 数据标准化
x = (x - x.mean()) / x.std()
# 将原始数据以散点图形式画出
plt.figure()
plt.scatter(x, y, c="g" ,s=6)
plt.show()
选择与训练模型
因为是线性回归问题,所以选择多项式拟合,其中f为模型,p,n分别为系数和指数,L为模型的损失函数,采用常用的平方误差函数,x,y分别为输入向量和目标向量,训练的过程其实就是最小化损失函数L的过程:

代码实现如下:
# 在(-2,4)区间取100个点作为画图的基础
x0 = np.linspace(-2, 4, 100)
# 利用Numpy的函数定义训练并返回多项式回归模型的函数
# deg参数代表模型参数的n,即多项式的次数
# 返回的模型能够根据输入的 x(默认是x0),返回相对应的预测的 y
def get_model(deg):
return lambda input_x = x0: np.polyval(np.polyfit(x, y, deg), input_x)
其中,polyfit(x,y,deg)返回使误差函数最小化的参数p,即多项式的系数,就是模型的训练函数;polyval(p,x)为模型函数,根据系数p和x的值,返回多项式结果值y。
评估并可视化结果
根据损失函数的值来评估模型的好坏,这里取n=1,4,10三个值,代码如下:
# 根据参数n,输入的x、y返回相对应的损失
def get_cost(deg, input_x, input_y):
return 0.5 * ((get_model(deg)(input_x) - input_y) ** 2).sum()
# 定义测试参数集并根据它进行各种实验
test_set = (1, 4, 10)
for d in test_set:
#输出相应损失
print(get_cost(d,x,y))
# 画出相应的图像
plt.scatter(x, y, c="g", s=20)
for d in test_set:
plt.plot(x0, get_model(d)(), label="degree = {}".format(d))
# 将横轴、纵轴的范围限制在(-2,4)、(100000,800000)
plt.xlim(-2,4)
plt.ylim(1e5,8e5)
# 调用legend方法使曲线对于的label正确显示
plt.legend()
plt.show()
结果如下图所示:
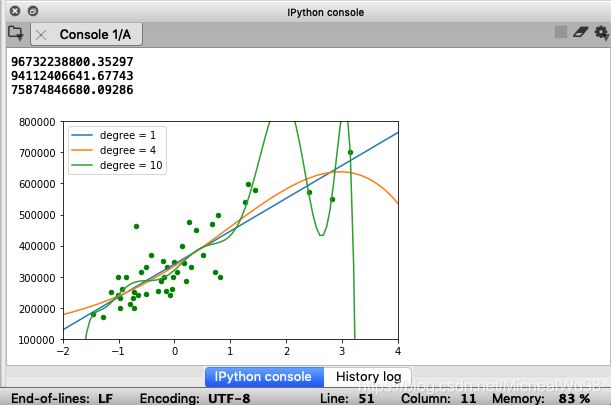
显然,从损失函数结果看,n=10优于n=4,n=1最差,但是从图中可得出,n=1是最好的情况,另外两种已经过拟合了。
收获
- 机器学习的基本过程是怎样的。
- Python的Numpy和Matplotlib库如何使用。
- 线性回归问题模型如何建立,输入数据如何标准化。
