python-opencv Harris 角点检测
1.目标
• 理解 Harris 角点检测的概念
• 学习函数:cv2.cornerHarris(),cv2.cornerSubPix()
2.原理
Harris 角点检测数学形式。将窗口向各个方向移动(u,v)然后计算所有差异的总和。表达式如下:

窗口函数可以是正常的矩形窗口也可以是对每一个像素给予不同权重的高斯窗口角点检测中要使 E (µ,ν) 的值最大。这就是说必须使方程右侧的第二项的取值最大。对上面的等式进行泰勒级数展开然后再通过几步数学换算(可以参考其他标准教材),我们得到下面的等式:
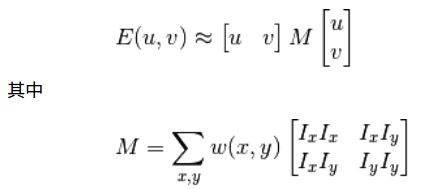
这里 I x 和 I y 是图像在 x 和 y 方向的导数。(可以使用函数 cv2.Sobel()
计算得到)。
然后就是主要部分了。他们根据一个用来判定窗口内是否包含角点的等式进行打分。
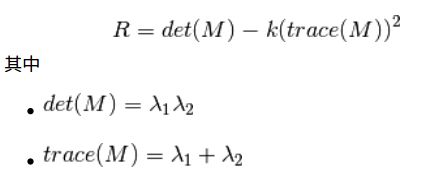
• λ 1 和 λ 2 是矩阵 M 的特征值所以根据这些特征中我们可以判断一个区域是否是角点,边界或者是平面。
• 当 λ 1 和 λ 2 都小时,|R| 也小,这个区域就是一个平坦区域。
• 当 λ 1 ≫ λ 2 或者 λ 1 ≪ λ 2 ,时 R 小于 0,这个区域是边缘
• 当 λ 1 和 λ 2 都很大,并且 λ 1 ~λ 2 中的时,R 也很大,(λ 1 和 λ 2 中的最小值都大于阈值)说明这个区域是角点。
可以用下图来表示我们的结论:

3.OpenCV 中的 Harris 角点检测
Open 中的函数 cv2.cornerHarris() 可以用来进行角点检测。参数如下:
• img - 数据类型为 float32 的输入图像。
• blockSize - 角点检测中要考虑的领域大小。
• ksize - Sobel 求导中使用的窗口大小
• k - Harris 角点检测方程中的自由参数,取值参数为 [0,04,0.06].
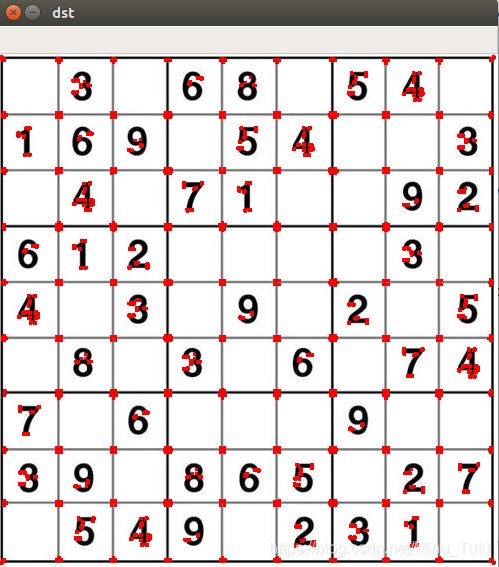
例子如下:
import cv2
import numpy as np
img = cv2.imread('shudu.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)
dst = cv2.cornerHarris(gray,2,3,0.04)
#result is dilated for marking the corners, not important
dst = cv2.dilate(dst,None)
# Threshold for an optimal value, it may vary depending on the image.
img[dst>0.01*dst.max()]=[0,0,255]
cv2.imshow('dst',img)
if cv2.waitKey(0) & 0xff == 27:
cv2.destroyAllWindows()
 4.亚像素级精确度的角点
4.亚像素级精确度的角点
有时我们需要最大精度的角点检测。OpenCV 为我们提供了函数 cv2.cornerSubPix(),它可以提供亚像素级别的角点检测。下面是一个例子。首先我们要找到 Harris角点,然后将角点的重心传给这个函数进行修正。Harris 角点用红色像素标出,绿色像素是修正后的像素。在使用这个函数是我们要定义一个迭代停止条件。当迭代次数达到或者精度条件满足后迭代就会停止。我们同样需要定义进行角点搜索的邻域大小。
import cv2
import numpy as np
filename = 'chessboard2.jpg'
img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# find Harris corners
gray = np.float32(gray)
dst = cv2.cornerHarris(gray,2,3,0.04)
dst = cv2.dilate(dst,None)
ret, dst = cv2.threshold(dst,0.01*dst.max(),255,0)
dst = np.uint8(dst)
# find centroids
ret, labels, stats, centroids = cv2.connectedComponentsWithStats(dst)
# define the criteria to stop and refine the corners
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.001)
corners = cv2.cornerSubPix(gray,np.float32(centroids),(5,5),(-1,-1),criteria)
# Now draw them
res = np.hstack((centroids,corners))
res = np.int0(res)
img[res[:,1],res[:,0]]=[0,0,255]
img[res[:,3],res[:,2]] = [0,255,0]
cv2.imwrite('subpixel5.png',img)
结果如下,为了方便查看我们对角点的部分进行了放大:
 5.Shi-Tomasi 角点检测 & 适合于跟踪的图像特征
5.Shi-Tomasi 角点检测 & 适合于跟踪的图像特征
目标
• 另外一个角点检测技术:Shi-Tomasi 焦点检测
• 函数:cv2.goodFeatureToTrack()
原理
我们学习了 Harris 角点检测,后来 1994 年,J.Shi 和 C.Tomasi在他们的文章《Good_Features_to_Track》中对这个算法做了一个小小的修改,并得到了更好的结果。我们知道 Harris 角点检测的打分公式为:
![]()
但 Shi-Tomasi 使用的打分函数为:
![]()
如果打分超过阈值,我们就认为它是一个角点。我们可以把它绘制到 λ 1 ~λ 2 空间中,就会得到下图:

从这幅图中,我们可以看出来只有当 λ 1 和 λ 2 都大于最小值时,才被认为是角点(绿色区域)。
cv2.goodFeaturesToTrack ( image, maxcorners, qualityLevel, minDistance, [, corners [, mask [, blocksize [, useHarrisDetector [, k ]]]]] )
maxCorners : 最大数目的角点数。即上文提到的N。
qualityLevel:该参数指出最低可接受的角点质量,是一个百分数,示例中给出为0.01。 具体来说,如果最好的角点质量=1500,而qualityLevel = 0.01,那么角点质量<15的就都会被拒掉。这里需要对角点质量如何得到进行简单说明。在官方的函数说明中,角点质量可由cornerHarris() 或 cornerMinEigenval() 得到,即两种quality measure。第一种cornerHarris()就是Harris角点检测的代码,函数返回每个像素点处计算出的R值,R值越大,认为角点质量越好;而cornerMinEigval()是计算每个像素点处对应的协方差矩阵的最小特征值,作为该像素点处的角点质量,认为最小特征值越大,角点质量越好(协方差矩阵就是Harris中提到的M,参考我另一篇博客)。
minDistance:角点之间最小的欧拉距离,避免得到相邻特征点。
import numpy as np
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('simple.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
corners = cv2.goodFeaturesToTrack(gray,25,0.01,10)
corners = np.int0(corners)
for i in corners:
x,y = i.ravel()
cv2.circle(img,(x,y),3,255,-1)
plt.imshow(img),plt.show()
