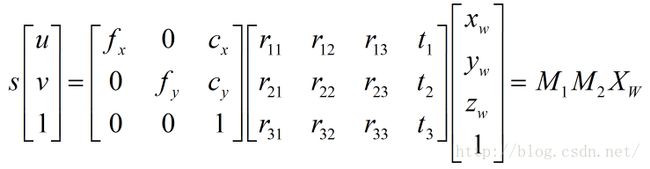基于Opencv2.4.11+OpenGL(Qt5.6.0)实现增强现实(四)
在进行下一步之前需要对相机进行标定,这里网上有很多标定的方案,本文采用的是基于平面方格点的方式求得相机的内参与畸变参数。求解的最终方程如下
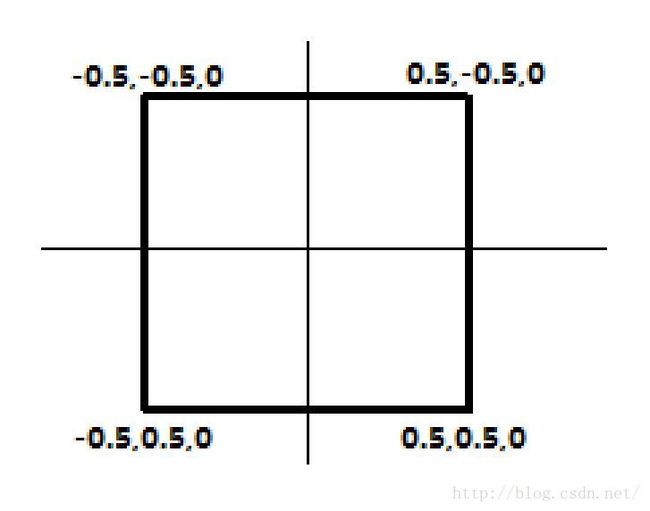
其中u,v为物体在成像面上的坐标,Xw为物体在世界坐标系中的坐标,M1为相机的内部参数,M2为相机的外部参数会随着物体的位置或者相机的位置的变换而变化。通过标定可以求得相机的内部参数矩阵与畸变参数。如果我们反过来进行思考,如果内部参数已知,物体在成像面上的坐标已知,不防假设某一个方块标记的中心位置为s世界坐标系的原点,物体所在位置Z轴为0,如下图所示,那么上式中的u,v已知,M1,Xw已知,即可求得M2即外部参数,从而可根据u,v确定特定物体的3D坐标,从而opengl就可以在特定位置实现3D物体的渲染,也就实现了增强现实的过程。也即每个标记对应一套坐标系,渲染的时候会以对应标记假定世界坐标系(x,y,0)为原点渲染3D物体,因此在之后实际渲染的过程中需要将物体沿Z轴向负向移动。而opencv中就有相应的函数求解,即solvePnP(),其参数见下方图片。
Xworld.push_back(Point3f(-0.5, -0.5, 0));
Xworld.push_back(Point3f(-0.5, 0.5, 0));
Xworld.push_back(Point3f(0.5, 0.5, 0));
Xworld.push_back(Point3f(0.5, -0.5, 0));
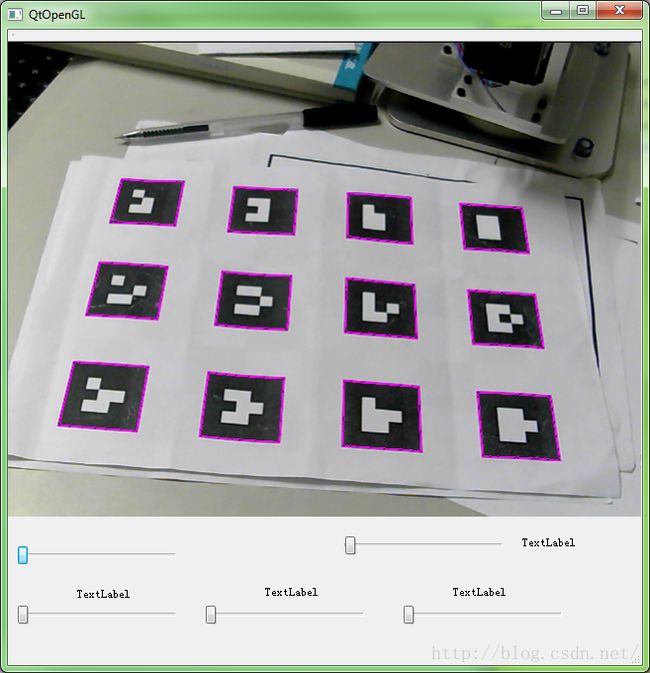
接下来的任务就很简单了,首先采用一种方法现对摄像头进行标定求得相机内部参数。之后就是通过图像处理对视野中的mark进行检测并对其四个点的位置坐标进行提取,图像处理采用基本的流程即先进行灰度转换再进行二值化处理,之后通过检测轮廓实现对一些噪点或者不规则的图像的过滤。处理过后基本可以确定所需区域。这里并没有对标记上的信息进行判断,检测出区域后很容易就可以判断标记上的信息,包括旋转等。之后就可以将参数代入函数中实现求解了。
由于opencv与opengl坐标系的差别需要绕X轴旋转180度,具体实现过程见代码。一切就绪后既可以得到所需的MODELVIEW矩阵了。由于不确定视场中标记的个数因此采用动态数组将采集到的MODELVIEW矩阵(4*4)放到动态容器中,之后通过循环处理在所有的标记上渲染3D物体。
void OpenGL::imageProcess(Mat image)
{
Mat grayImage,tempImage;
cvtColor(image,grayImage,CV_BGR2GRAY);
adaptiveThreshold(grayImage, tempImage, 255, ADAPTIVE_THRESH_GAUSSIAN_C, CV_THRESH_BINARY_INV, 7, 7);
//imshow("二值化",tempImage);
vector> all_contours;
vector> contours;
//Rect RectArea;
findContours(tempImage, all_contours, CV_RETR_LIST, CV_CHAIN_APPROX_NONE);
for (int i = 0; i < all_contours.size(); ++i)
{
if (all_contours[i].size() > 100)
{
contours.push_back(all_contours[i]);
//drawContours(frame,all_contours,i,Scalar(0,0,255),1,8);
}
}
vector approxCurve;//返回结果为多边形,用点集表示//相似形状
for (size_t i = 0; i < contours.size(); i++)
{
double eps = contours[i].size()*0.05;
//输入图像的2维点集,输出结果,估计精度,是否闭合。输出多边形的顶点组成的点集/approxPolyDP(contours[i], approxCurve, eps, true);
//我们感兴趣的多边形只有四个顶点
if (approxCurve.size() != 4)
continue;
//检查轮廓是否是凸边形
if (!isContourConvex(approxCurve))
continue;
//确保连续点之间的距离是足够大的。//确保相邻的两点间的距离“足够大”-大到是一条边而不是短线段就是了
//float minDist = numeric_limits::max();//代表float可以表示的最大值,numeric_limits就是模板类,这里表示max(float);3.4e038
float minDist = 1e10;//这个值就很大了
//求当前四边形各顶点之间的最短距离
for (int j = 0; j < 4; j++)
{
Point side = approxCurve[j] - approxCurve[(j + 1) % 4];//这里应该是2维的相减
float squaredSideLength = side.dot(side);//求2维向量的点积,就是XxY
minDist = min(minDist, squaredSideLength);//找出最小的距离
}
//检查距离是不是特别小,小的话就退出本次循环,开始下一次循环
if (minDist < MIN_LENGTH*MIN_LENGTH)
continue;
//所有的测试通过了,保存标识候选,当四边形大小合适,则将该四边形maker放入possibleMarkers容器内 //保存相似的标记
drawContours(frame, contours, i, Scalar(255, 0, 255), 1, 8);
for (int j = 0; j < 4; j++){
Ximage.push_back(approxCurve[j]);}
// Sort the points in anti - clockwise
Point2f v1 = Ximage[1] - Ximage[0];
Point2f v2 = Ximage[2] - Ximage[0];
if (v1.cross(v2) > 0) //由于图像坐标的Y轴向下,所以大于零才代表逆时针
{
swap(Ximage[1], Ximage[3]);
}
//possible_markers.push_back(marker);
Mat rvec, tvec;
solvePnP(Xworld, Ximage, cameraMatrix, distCoeffs, rvec,tvec);
Mat rmat ;
Rodrigues(rvec, rmat);
//绕X轴旋转180度,从OpenCV坐标系变换为OpenGL坐标系
static double d[] =
{
1, 0, 0,
0,-1, 0,
0, 0, -1
};
Mat_ rx(3, 3, d);
rmat = rx*rmat;
tvec = rx*tvec;
rotMatrix.push_back(rmat.at(0, 0));
rotMatrix.push_back(rmat.at(1, 0));
rotMatrix.push_back(rmat.at(2, 0));
rotMatrix.push_back(0.0f);
rotMatrix.push_back(rmat.at(0, 1));
rotMatrix.push_back(rmat.at(1, 1));
rotMatrix.push_back(rmat.at(2, 1));
rotMatrix.push_back(0.0f);
rotMatrix.push_back(rmat.at(0, 2));
rotMatrix.push_back(rmat.at(1, 2));
rotMatrix.push_back(rmat.at(2, 2));
rotMatrix.push_back(0.0f);
rotMatrix.push_back(tvec.at(0, 0));
rotMatrix.push_back(tvec.at(1, 0));
rotMatrix.push_back(tvec.at(2, 0));
rotMatrix.push_back(1.0f);
RotationMatrix.push_back(rotMatrix);
Ximage.clear();
rotMatrix.clear();
}
}
之后还需要计算出正确的OPENGL投影矩阵,计算的公式可以参考(一)中开始提到的博客,这里直接给出代码,初始化的时候加载该投影矩阵即可。
glLoadIdentity();
glMatrixMode(GL_PROJECTION);//选择矩阵模式
double f_x = cameraMatrix.at(0, 0);
double f_y = cameraMatrix.at(1, 1);
double c_x = cameraMatrix.at(0, 2);
double c_y = cameraMatrix.at(1, 2);
projection_matrix[0] = 2 * f_x / IMAGE_WIDTH;
projection_matrix[1] = 0.0f;
projection_matrix[2] = 0.0f;
projection_matrix[3] = 0.0f;
projection_matrix[4] = 0.0f;
projection_matrix[5] = 2 * f_y / IMAGE_HEIGHT;
projection_matrix[6] = 0.0f;
projection_matrix[7] = 0.0f;
projection_matrix[8] = 1.0f - 2 * c_x / IMAGE_WIDTH;
projection_matrix[9] = 2 * c_y / IMAGE_HEIGHT - 1.0f;
projection_matrix[10] = -(0.01f + 100.0f) / (100.0f - 0.01f);
projection_matrix[11] = -1.0f;
projection_matrix[12] = 0.0f;
projection_matrix[13] = 0.0f;
projection_matrix[14] = -2.0f * 100 * 0.01 / (100.0f - 0.01f);
projection_matrix[15] = 0.0f;
glMultMatrixf(projection_matrix); 这样整个过程就走完了,至于判断标记上的信息及转动角度并不是最大的难点。本人刚开始调试的时候急于求成,希望能直接拿别人的代码过来跑但是结果是各种错误。因此在看到开篇的那段公式之后才恍然大悟,按照自己的思路参考前人的代码实现自己的工程我想这样才能真的学有所获。
最终上传下工程文件,不足之处还请斧正,点击下载。