图像到图像的映射(一)
实验目标:使用仿射变换将一张图像放置到另一幅图像中
1.计算第二张图像与第一张图像之间的变换关系
2.将第二张图像叠加到(通过设置α通道的值)第一张图像的坐标系中
3.变换后的融合/合成
1.原理
单应性变换(Homography)
将平面内一个点映射到另一个平面内的二维投影变换。单应性矩阵H具有8个独立的自由度,其中h33=1。H的求解在代码中的Haffine_from_points(在homography.py中)
( x ′ y ′ w ′ ) = ( h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ) ( x y w ) \begin{pmatrix} x'\\ y'\\ w' \end{pmatrix}=\begin{pmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33} \end{pmatrix} \begin{pmatrix} x\\ y\\ w \end{pmatrix} ⎝⎛x′y′w′⎠⎞=⎝⎛h11h21h31h12h22h32h13h23h33⎠⎞⎝⎛xyw⎠⎞
单应性矩阵可以由两幅图像中对应点计算出来。然后我们再得到坐标的变换公式。
矩阵H会将一幅图像上的一个点的坐标a=(x,y,1)映射成另一幅图像上的点的坐标b=(x1,y1,1),也就是说,我们已知a和b,它们是在同一平面上,代码里是将fp对应到tp(映射目标点)。 则有下面的公式(1):
b = H ∗ a T b =H*a^{T} b=H∗aT
即:
{ x 1 = h 11 x + h 12 y + h 13 . . . . . . . . ① y 1 = h 21 x + h 22 y + h 23 . . . . . . . . ② 1 = h 31 x + h 32 y + h 33 . . . . . . . . ③ \left\{\begin{matrix} x_{1}= &h_{11}x + &h_{12}y + &h_{13} ........① \\ y_{1}= &h_{21}x + &h_{22}y + &h_{23} ........②\\ 1 = &h_{31}x + &h_{32}y + &h_{33}........③ \end{matrix}\right. ⎩⎨⎧x1=y1=1=h11x+h21x+h31x+h12y+h22y+h32y+h13........①h23........②h33........③
由上面的公式中的③可以得到坐标变换的公式
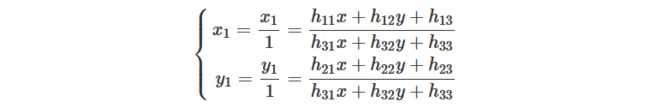 继续得:
继续得:
 根据前面式子(1)可写成一个矩阵与一个向量相乘,即得到式子(2):
根据前面式子(1)可写成一个矩阵与一个向量相乘,即得到式子(2):
 其中,h=[h11,h12,h13,h21,h22,h23,h31,h32,h33]^T,是一个9维的列向量。若令:
其中,h=[h11,h12,h13,h21,h22,h23,h31,h32,h33]^T,是一个9维的列向量。若令:
 然后又几对匹配特征就会几个A矩阵,n为匹配特征的对数,单应性矩阵有里8个自由度,至少需要4对(且要求三点不共线,所以这里选择四边形的四个顶点)
然后又几对匹配特征就会几个A矩阵,n为匹配特征的对数,单应性矩阵有里8个自由度,至少需要4对(且要求三点不共线,所以这里选择四边形的四个顶点)

则式子(2)可记做:
A h = 0 Ah=0 Ah=0
可以用SVD算法找到h的最小二乘解(具体参考这篇博文,讲解详细:https://www.cnblogs.com/pinard/p/6251584.html)。
我们把矩阵A的SVD定义为
A = U D V T A=UDV^{T} A=UDVT
V的最后一行是h的一个解
即有两个解,
{ h = 0 , A T A 的 特 征 向 量 \left\{\begin{matrix} h=0 ,\\ A^{T}A的特征向量\\ \end{matrix}\right. {h=0,ATA的特征向量
仿射变换(affine)
一种二维坐标到二维坐标之间的线性变换(相同平面),它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变),但是角度会改变。任意的仿射变换都能表示为乘以一个矩阵(线性变换),再加上一个向量 (平移) 的形式。
单应性变换有8个自由度,仿射有6个自由度
我们令H矩阵的 h31=h32=0,即:

仿射变换具有6个自由度,因此我们需要三个对应点来估计矩阵H。
α通道
阿尔法通道是一个8位的灰度通道,该通道用256级灰度来记录图像中的透明度信息,定义透明、不透明和半透明区域,其中0表示透明,1表示不透明,0-1区间表示半透明,因为阿尔法通道有8bit可以有256种不同的数据表示可能性。相当于Photoshop中的蒙版的作用:在当前图层上面覆盖一层玻璃片,这种玻璃片有透明的、半透明的、完全不透明的。
举个栗子:
我们是要把im1放置在im2上得到im3
若alpha=0代表im1_1对应位置上显示为透明,即不显示im1的颜色,1-alpha=1代表im2显示为原本的颜色。
# alpha for triangle
#创建大小(m,n)的alpha集合 对于由点定义的角的三角形 (以归一化齐次坐标给出)。
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
2.实验中遇到的问题以及解决
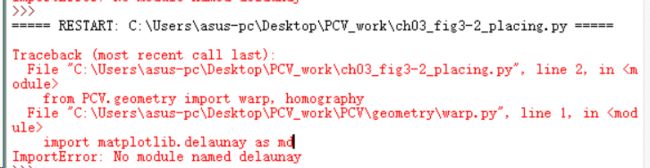 提示错误:
提示错误:
No module named delaunay
因为在warp.py的源码是
#import matplotlib.delaunay as md
但是因为新的scipy中的Delaunay被放在saptial下面了
所以
改为:from scipy.spatial import Delaunay
就可以了。
3.代码
手动找坐标点太不方便,接下来是获取点坐标的代码
# coding: utf-8
import cv2
img = cv2.imread("C:/Users/asus-pc/Desktop/PCV_work/2a.jpg")
# print img.shape
def on_EVENT_LBUTTONDOWN(event, x, y, flags, param):
if event == cv2.EVENT_LBUTTONDOWN:
xy = "%d,%d" % (x, y)
cv2.circle(img, (x, y), 1, (255, 0, 0), thickness=-1)
cv2.putText(img, xy, (x, y), cv2.FONT_HERSHEY_PLAIN,
1.0, (0, 0, 0), thickness=1)
cv2.imshow("image", img)
cv2.namedWindow("image")
cv2.setMouseCallback("image", on_EVENT_LBUTTONDOWN)
cv2.imshow("image", img)
while (True):
try:
cv2.waitKey(100)
except Exception:
cv2.destroyAllWindows()
break
cv2.waitKey(0)
cv2.destroyAllWindows()
获取结果如下:
placing.py
# -*- coding: utf-8 -*-
#主程序
from PCV.geometry import warp, homography
from PIL import Image
from pylab import *
from scipy import ndimage
# example of affine warp of im1 onto im2
#读取两张图片做二值化处理
im1 = array(Image.open('p3.jpg').convert('L'))
im2 = array(Image.open('p4.jpg').convert('L'))
'''预先获取坐标位置,第一列为从左上角开始为逆时针四点的y轴坐标
(我们选取正下为y轴),第二列为对应x坐标'''
#tp是映射目标位置
#tp = array([[423,491,497,424],[512,506,809,807],[1,1,1,1]])
tp = array([[369,598,575,326],[512,481,803,782],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
figure()
gray()
subplot(221)
axis('off')
imshow(im1)
subplot(222)
axis('off')
imshow(im2)
subplot(223)
axis('off')
imshow(im3)
#下面是三角形仿射
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# 计算 H
H = homography.Haffine_from_points(tp2,fp2)
#计算H,fp映射到tp,其中tp是映射目标位置
#扭曲操作,直接使用Scipy工具包来完成
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
#H[:2,:2]是因为仿射仅取H的前两列
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
#
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# 计算 H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(224)
imshow(im4)
axis('off')
show()
homography.py
# -*- coding: utf-8 -*-
from numpy import *
from scipy import ndimage
class RansacModel(object):
""" Class for testing homography fit with ransac.py from
http://www.scipy.org/Cookbook/RANSAC"""
def __init__(self,debug=False):
self.debug = debug
def fit(self, data):
""" Fit homography to four selected correspondences. """
# transpose to fit H_from_points()
data = data.T
# from points
fp = data[:3,:4]
# target points
tp = data[3:,:4]
# fit homography and return
return H_from_points(fp,tp)
def get_error( self, data, H):
""" 将单应性矩阵的每个转换点的返回错误。 """
data = data.T
# from points
fp = data[:3]
# target points
tp = data[3:]
# transform fp
fp_transformed = dot(H,fp)
# normalize hom. coordinates
fp_transformed = normalize(fp_transformed)
# return error per point
return sqrt( sum((tp-fp_transformed)**2,axis=0) )
def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
""" Robust estimation of homography H from point
correspondences using RANSAC (ransac.py from
http://www.scipy.org/Cookbook/RANSAC).
input: fp,tp (3*n arrays) points in hom. coordinates. """
from PCV.tools import ransac
# group corresponding points
data = vstack((fp,tp))
# compute H and return
H,ransac_data = ransac.ransac(data.T,model,4,maxiter,match_theshold,10,return_all=True)
return H,ransac_data['inliers']
def H_from_points(fp,tp):
""" 用DLT直接线性变换计算fp映射到tp,点归一化 """
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
# 对点归一化
# --映射起始点--
m = mean(fp[:2], axis=1)
maxstd = max(std(fp[:2], axis=1)) + 1e-9
C1 = diag([1/maxstd, 1/maxstd, 1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp = dot(C1,fp)
# --映射对应点--
m = mean(tp[:2], axis=1)
maxstd = max(std(tp[:2], axis=1)) + 1e-9
C2 = diag([1/maxstd, 1/maxstd, 1])
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp = dot(C2,tp)
# create matrix for linear method, 2 rows for each correspondence pair
nbr_correspondences = fp.shape[1]
A = zeros((2*nbr_correspondences,9))
for i in range(nbr_correspondences):
A[2*i] = [-fp[0][i],-fp[1][i],-1,0,0,0,
tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1,
tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
U,S,V = linalg.svd(A)
H = V[8].reshape((3,3))
# 反归一化
H = dot(linalg.inv(C2),dot(H,C1))
# normalize and return
return H / H[2,2]
def Haffine_from_points(fp,tp):
""" Find H, affine transformation, such that
tp is affine transf of fp. """
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
# condition points
# --from points--
m = mean(fp[:2], axis=1)
maxstd = max(std(fp[:2], axis=1)) + 1e-9
C1 = diag([1/maxstd, 1/maxstd, 1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp_cond = dot(C1,fp)
# --to points--
m = mean(tp[:2], axis=1)
C2 = C1.copy() #must use same scaling for both point sets
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp_cond = dot(C2,tp)
# conditioned points have mean zero, so translation is zero
A = concatenate((fp_cond[:2],tp_cond[:2]), axis=0)
U,S,V = linalg.svd(A.T)
# create B and C matrices as Hartley-Zisserman (2:nd ed) p 130.
tmp = V[:2].T
B = tmp[:2]
C = tmp[2:4]
tmp2 = concatenate((dot(C,linalg.pinv(B)),zeros((2,1))), axis=1)
H = vstack((tmp2,[0,0,1]))
# decondition
H = dot(linalg.inv(C2),dot(H,C1))
return H / H[2,2]
def normalize(points):
""" Normalize a collection of points in
homogeneous coordinates so that last row = 1. """
for row in points:
row /= points[-1]
return points
def make_homog(points):
""" Convert a set of points (dim*n array) to
homogeneous coordinates. """
return vstack((points,ones((1,points.shape[1]))))
warp.py
# -*- coding: utf-8 -*-
#import matplotlib.delaunay as md
from scipy.spatial import Delaunay
from scipy import ndimage
from pylab import *
from numpy import *
from PCV.geometry import homography
def image_in_image(im1,im2,tp):
""" 使用仿射变换将im1放置在im2上,
使得im1图像的左上角和tp(映射目标的位置)尽可能靠近
fp是im2"""
# points to warp from
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
#n是im2投影到im1的图像的长,m是宽
#im1四个顶点的坐标
# 得到单应性矩阵
H = homography.Haffine_from_points(tp,fp)
#两个图形的变换关系(位移+缩放),只取H的前两行
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
alpha = (im1_t > 0)
return (1-alpha)*im2 + alpha*im1_t
def combine_images(im1,im2,alpha):
""" Blend two images with weights as in alpha. """
return (1-alpha)*im1 + alpha*im2
def alpha_for_triangle(points,m,n):
""" Creates alpha map of size (m,n)
for a triangle with corners defined by points
(given in normalized homogeneous coordinates). """
alpha = zeros((m,n))
for i in range(min(points[0]),max(points[0])):
for j in range(min(points[1]),max(points[1])):
x = linalg.solve(points,[i,j,1])
if min(x) > 0: #all coefficients positive
alpha[i,j] = 1
return alpha
def triangulate_points(x,y):
""" Delaunay triangulation of 2D points. """
centers,edges,tri,neighbors = md.delaunay(x,y)
return tri
def plot_mesh(x,y,tri):
""" Plot triangles. """
for t in tri:
t_ext = [t[0], t[1], t[2], t[0]] # add first point to end
plot(x[t_ext],y[t_ext],'r')
def pw_affine(fromim,toim,fp,tp,tri):
""" Warp triangular patches from an image.
fromim = image to warp
toim = destination image
fp = from points in hom. coordinates
tp = to points in hom. coordinates
tri = triangulation. """
im = toim.copy()
# check if image is grayscale or color
is_color = len(fromim.shape) == 3
# create image to warp to (needed if iterate colors)
im_t = zeros(im.shape, 'uint8')
for t in tri:
# compute affine transformation
H = homography.Haffine_from_points(tp[:,t],fp[:,t])
if is_color:
for col in range(fromim.shape[2]):
im_t[:,:,col] = ndimage.affine_transform(
fromim[:,:,col],H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
else:
im_t = ndimage.affine_transform(
fromim,H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
# alpha for triangle
alpha = alpha_for_triangle(tp[:,t],im.shape[0],im.shape[1])
# add triangle to image
im[alpha>0] = im_t[alpha>0]
return im
def panorama(H,fromim,toim,padding=2400,delta=2400):
""" Create horizontal panorama by blending two images
using a homography H (preferably estimated using RANSAC).
The result is an image with the same height as toim. 'padding'
specifies number of fill pixels and 'delta' additional translation. """
# check if images are grayscale or color
is_color = len(fromim.shape) == 3
# homography transformation for geometric_transform()
def transf(p):
p2 = dot(H,[p[0],p[1],1])
return (p2[0]/p2[2],p2[1]/p2[2])
if H[1,2]<0: # fromim is to the right
print 'warp - right'
# transform fromim
if is_color:
# pad the destination image with zeros to the right
toim_t = hstack((toim,zeros((toim.shape[0],padding,3))))
fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
for col in range(3):
fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
transf,(toim.shape[0],toim.shape[1]+padding))
else:
# pad the destination image with zeros to the right
toim_t = hstack((toim,zeros((toim.shape[0],padding))))
fromim_t = ndimage.geometric_transform(fromim,transf,
(toim.shape[0],toim.shape[1]+padding))
else:
print 'warp - left'
# add translation to compensate for padding to the left
H_delta = array([[1,0,0],[0,1,-delta],[0,0,1]])
H = dot(H,H_delta)
# transform fromim
if is_color:
# pad the destination image with zeros to the left
toim_t = hstack((zeros((toim.shape[0],padding,3)),toim))
fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
for col in range(3):
fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
transf,(toim.shape[0],toim.shape[1]+padding))
else:
# pad the destination image with zeros to the left
toim_t = hstack((zeros((toim.shape[0],padding)),toim))
fromim_t = ndimage.geometric_transform(fromim,
transf,(toim.shape[0],toim.shape[1]+padding))
# blend and return (put fromim above toim)
if is_color:
# all non black pixels
alpha = ((fromim_t[:,:,0] * fromim_t[:,:,1] * fromim_t[:,:,2] ) > 0)
for col in range(3):
toim_t[:,:,col] = fromim_t[:,:,col]*alpha + toim_t[:,:,col]*(1-alpha)
else:
alpha = (fromim_t > 0)
toim_t = fromim_t*alpha + toim_t*(1-alpha)
return toim_t
实验结果:
使用仿射变换将im1放置在im2上:
(2 2 1)是im1 ,(2 2 2)是im2,
(2 2 3)是仿射,(2 2 4)是三角形的仿射弯曲效果(下篇解释)
把光前体院馆换成美岭楼的名字
在建安楼投上照片
