图像特征检测——Harris角点检测

图像特征检测——Harris角点检测

一、Harris角点检测

（1）原理
通过一个小窗口对图像进行积分，随着窗口的移动，根据窗口内像素灰度积分值来判断像素点是否为角点，依据如下：

• 灰度变化平缓的地方，窗口向任何方向移动，灰度积分保持不变，定义为“flat”
• 图像边缘区域，窗口沿着边缘移动时，灰度积分近似不变，沿着其他方向移动时，灰度积分变化剧烈，定义为“edge”
• 在角点处，窗口向任何方向移动，灰度积分都会剧烈变化，定义为“corner”

（2）灰度积分变化
定义灰度积分变化为$$E(u,v)=\Sigma w(x,y)[I(x+u,y+v)-I(x,y){]}^2$$其中

$\Sigma [I(x+u,y+v)-I(x,y){]}^2\approx \Sigma [I(x,y)+u{I}_x+v{I}_y-I(x,y)]$

$$=\Sigma u^2{I}_x^2+2uv{I}_x{I}_y+v^2{I}_y^2$$

$$=\Sigma \left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]$$

$$=\left[\begin{array}{cc}u& v\end{array}\right](\Sigma \left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right])\left[\begin{array}{c}u\\ v\end{array}\right]$$
当窗口移动的距离很小的时候，即$(u,v)$的变换很小，则有
$$E(u,v)=\left[\begin{array}{cc}u& v\end{array}\right]M\left[\begin{array}{c}u\\ v\end{array}\right]$$其中，$$M=\Sigma w(x,y)\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]$$
可以发现，$E$是一个二次型，可以化简为$$E=\left[\begin{array}{cc}u& v\end{array}\right]\left[\begin{array}{cc}A& C\\ C& B\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]=A{u}^2+B{v}^2+2Cuv$$
等效为椭圆模型，则为
$$u^2/a^2+v^2/b^2=1$$

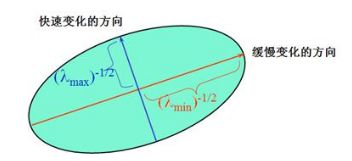
（3）Harris算子

${\lambda }_1^{-1/2}$和${\lambda }_2^{-1/2}$是椭圆的长短轴

• 当${\lambda }_1和{\lambda }_2$都比较小时，点$(x,y)$处于“flat”区域.
• 当${\lambda }_1>>{\lambda }_2$或者${\lambda }_1<<{\lambda }_2$时，点$(x,y)$处于“edge”区域.
• 当${\lambda }_1和{\lambda }_2$都比较大时，点$(x,y)$为“orner”.

（4）角点响应函数
上一点说的${\lambda }_1和{\lambda }_2$比较小和比较大是一个相对值，在实际检测中是无法有效界定的，因此，Harris算子引入角点响应函数来判断像素点的类型
$$R=detM-k(traceM{)}^2$$$$traceM={\lambda }_1+{\lambda }_2$$$$detM={\lambda }_1{\lambda }_2$$

• 当$R$接近于零时，处于灰度变化平缓的“flat”区域
• 当$R<0$时，点为边缘“edge”像素
• 当$R>0$时，点为角点“corner”

（5）opencv Harris角点检测函数

C++:
void cv::cornerHarris	(	InputArray 	src,			# 输入图像，单通道-8位或者浮点型图像
				OutputArray 	dst,		# 输出图像，保存Harris角点检测结果，和源图像尺寸一样
				int 	blockSize,				# 邻域的大小
				int 	ksize,						# Sobel算子的孔径大小
				double 	k,					# 角点响应函数的参数k
				int 	borderType = BORDER_DEFAULT 		# 图像像素的边界模式
				)	
	
Python:
dst	=	cv.cornerHarris(	src, blockSize, ksize, k[, dst[, borderType]]	)

二、python实现Harris角点检测

import cv2 as cv
import numpy as np

# Harris method
lena = cv.imread("/home/lihoon/code/opencvImg/Harris/lena.jpg")
gray_lena = cv.cvtColor(lena, cv.COLOR_BGR2GRAY)
gray_lena = np.float32(gray_lena)

dst = cv.cornerHarris(gray_lena, 3, 3, 0.05)
lena[dst > 0.01 * dst.max()] = [0, 0, 255]

cv.imshow("Harris", lena)

cv.waitKey()

图中，红色的点就是通过Harris角点检测算子检测的特征点