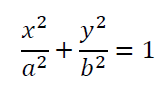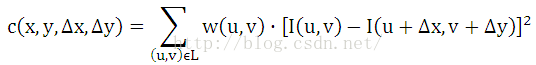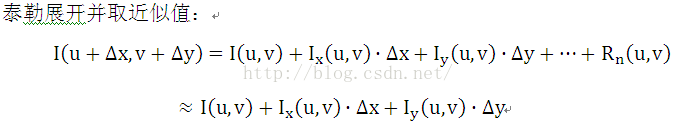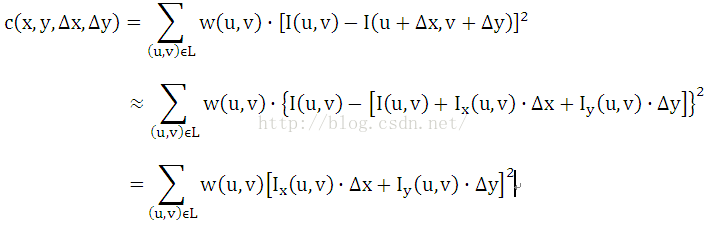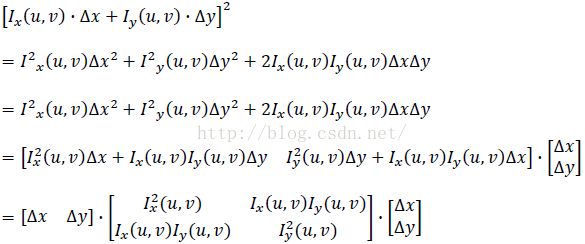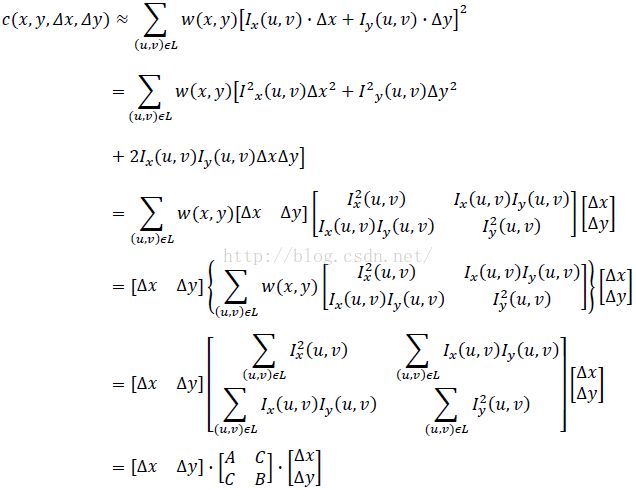特征点检测学习_3(Harris算法)
角点的定义
角点可以认为是图像亮度变化剧烈的点或图像边缘曲线上曲率极大值的点
角点就是极值点,在某个方面属性特别突出的点
角点可以是两条线的交叉处,也可以是位于相邻的两个主要方向不同的事物上的点
角点:最直观的印象就是在水平,垂直两个方向上变化均较大的点
边缘:仅在水平、或者垂直方向上有较大变化
平坦地区:在水平、垂直方向的变化量均较小
角点检测
角点检测是获取图像特征的一种方法,广泛用于运动检测,图像匹配,视觉跟踪,三维建模和目标识别等领域。也称为特征点检测
角点检测算法可以归为三类:
基于灰度图像的角点检测
基于二值图像的角点检测
基于轮廓曲线的角点检测
其中,基于灰度图像的角点检测又分为基于梯度,基于模板和基于模板梯度组合三类方法。其中基于模板的方法主要考虑像素领
域点的灰度变化,即图像亮度的变化,将与邻点亮度对比足够大的点定义为角点。
常见的基于模板的角点检测算法有:
Kitchen-Rosenfeld角点检测
Harris角点检测
KLT角点检测
SUSAN角点检测
下面重点介绍一下Harris角点检测的数学原理以实现过程
数学推导过程
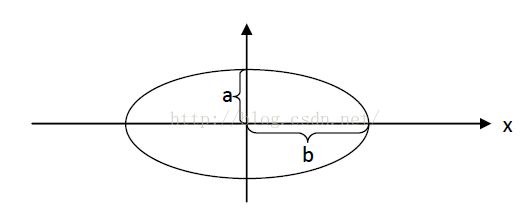
1.椭圆的矩阵方程表示
这是标准椭圆及其方程式,如果将上述方程写成矩阵形式:
2.椭圆半轴与特征值的关系
如果求上述方程式的特征值,则可以得到特征值与椭圆半轴的关系,推导过程如下:
Harris角点检测数学推导过程
Harris算法是利用的窗口内图像灰度的自相关性进行的,设定一个窗口,并在图像中移动,计算移动前与移动后窗口所在区域图
像的自相关系数。
自相关函数计算如下,(x,y)为窗口中心位置,w(u,v)为权重(一般取高斯函数),L表示窗口,(u,v)表示窗口中的图像位置:
将近似值代入自相关函数,有:
将平方项展开并写成矩阵形式,有:
回到自相关表达式:
经过上面的数学形式推导,已经得到了自相关函数的表达式。可以看得这也是一个椭圆的矩阵表示形式(非标准椭圆),因此其系
数矩阵M的特征值与椭圆的半轴长短有关,这与上面预备知识中的结论一样。
假设M的特征值为λ1、λ2,则分以下三种情况:
通过上面的情况,计算出特征值后就可以判别是否是角点了。
当然,这样计算量非常大,因为图像中的几乎每个点都需要进行一次特征值的计算;下面给出一个经验公式:
detM表示M的行列式,traceM表示M的迹,R表示角点响应值。α为经验常数,一般在0.04至0.06之间取值。
detM = λ1*λ2 = AB - C*C;
tracM = λ1 + λ2 = A+B;
判断准则:当R超过某个设定的阈值时,可认为是角点;反之,则不是。
Harris角点检测实现步骤

/*
int block_size: 邻域大小,相邻像素的尺寸,就是窗口函数大小 W(x, y);
int aperture_size: aperture size for the Sobel(); 因为我们用sobel函数来得到Ix, Iy;
double k : harris 检测器的自由参数
*/
cvCornerHarris( const CvArr* srcarr, CvArr* dstarr,
int block_size, int aperture_size, double k )
{
cv::Mat src = cv::cvarrToMat(srcarr), dst = cv::cvarrToMat(dstarr);
CV_Assert( src.size() == dst.size() && dst.type() == CV_32FC1 );
//调用opencv内部Harris检测函数
cv::cornerHarris( src, dst, block_size, aperture_size, k, cv::BORDER_REPLICATE );
}
//分配输出数据空间,并调用harris特征检测函数
void cv::cornerHarris( InputArray _src, OutputArray _dst, int blockSize, int ksize, double k, int borderType )
{
Mat src = _src.getMat();
_dst.create( src.size(), CV_32F );
Mat dst = _dst.getMat();
cornerEigenValsVecs( src, dst, blockSize, ksize, HARRIS, k, borderType );
}
//预处理:sobel检测获取x方向和y方向上的边缘, 滤波处理,准备好Ix*Ix Iy*Iy Ix*Iy
//然后调用最终的检测函数
static void
cornerEigenValsVecs( const Mat& src, Mat& eigenv, int block_size,
int aperture_size, int op_type, double k=0.,
int borderType=BORDER_DEFAULT )
{
#ifdef HAVE_TEGRA_OPTIMIZATION
if (tegra::cornerEigenValsVecs(src, eigenv, block_size, aperture_size, op_type, k, borderType))
return;
#endif
int depth = src.depth();
double scale = (double)(1 << ((aperture_size > 0 ? aperture_size : 3) - 1)) * block_size;
if( aperture_size < 0 )
scale *= 2.;
if( depth == CV_8U )
scale *= 255.;
scale = 1./scale;
CV_Assert( src.type() == CV_8UC1 || src.type() == CV_32FC1 );
Mat Dx, Dy;
if( aperture_size > 0 ) //利用sobel获取图像边缘信息,获取x和y两个方向的边缘信息
{
Sobel( src, Dx, CV_32F, 1, 0, aperture_size, scale, 0, borderType );
Sobel( src, Dy, CV_32F, 0, 1, aperture_size, scale, 0, borderType );
}
else
{
Scharr( src, Dx, CV_32F, 1, 0, scale, 0, borderType );
Scharr( src, Dy, CV_32F, 0, 1, scale, 0, borderType );
}
Size size = src.size();
Mat cov( size, CV_32FC3 );
int i, j;
for( i = 0; i < size.height; i++ )
{
float* cov_data = (float*)(cov.data + i*cov.step);
const float* dxdata = (const float*)(Dx.data + i*Dx.step);
const float* dydata = (const float*)(Dy.data + i*Dy.step);
for( j = 0; j < size.width; j++ )
{
float dx = dxdata[j];
float dy = dydata[j];
cov_data[j*3] = dx*dx;
cov_data[j*3+1] = dx*dy;
cov_data[j*3+2] = dy*dy;
}
}
//使用方框滤波
boxFilter(cov, cov, cov.depth(), Size(block_size, block_size),
Point(-1,-1), false, borderType );
//这里有几种方式
if( op_type == MINEIGENVAL )
calcMinEigenVal( cov, eigenv );
else if( op_type == HARRIS )
calcHarris( cov, eigenv, k );
else if( op_type == EIGENVALSVECS )
calcEigenValsVecs( cov, eigenv );
}
//特征提取函数
static void
calcHarris( const Mat& _cov, Mat& _dst, double k )
{
int i, j;
Size size = _cov.size();
#if CV_SSE
volatile bool simd = checkHardwareSupport(CV_CPU_SSE);
#endif
if( _cov.isContinuous() && _dst.isContinuous() )
{
size.width *= size.height;
size.height = 1;
}
for( i = 0; i < size.height; i++ )
{
const float* cov = (const float*)(_cov.data + _cov.step*i);
float* dst = (float*)(_dst.data + _dst.step*i);
j = 0;
#if CV_SSE
if( simd )
{
__m128 k4 = _mm_set1_ps((float)k);
for( ; j <= size.width - 5; j += 4 )
{
__m128 t0 = _mm_loadu_ps(cov + j*3); // a0 b0 c0 x
__m128 t1 = _mm_loadu_ps(cov + j*3 + 3); // a1 b1 c1 x
__m128 t2 = _mm_loadu_ps(cov + j*3 + 6); // a2 b2 c2 x
__m128 t3 = _mm_loadu_ps(cov + j*3 + 9); // a3 b3 c3 x
__m128 a, b, c, t;
t = _mm_unpacklo_ps(t0, t1); // a0 a1 b0 b1
c = _mm_unpackhi_ps(t0, t1); // c0 c1 x x
b = _mm_unpacklo_ps(t2, t3); // a2 a3 b2 b3
c = _mm_movelh_ps(c, _mm_unpackhi_ps(t2, t3)); // c0 c1 c2 c3
a = _mm_movelh_ps(t, b);
b = _mm_movehl_ps(b, t);
t = _mm_add_ps(a, c);
a = _mm_sub_ps(_mm_mul_ps(a, c), _mm_mul_ps(b, b));
t = _mm_mul_ps(_mm_mul_ps(k4, t), t);
a = _mm_sub_ps(a, t);
_mm_storeu_ps(dst + j, a);
}
}
#endif
for( ; j < size.width; j++ )
{
float a = cov[j*3];
float b = cov[j*3+1];
float c = cov[j*3+2];
dst[j] = (float)(a*c - b*b - k*(a + c)*(a + c)); //对应公式
}
}
}