算法导论习题解-第22章基本的图算法

总结

深度优先搜索

按照访问顺序，每个顶点标记两个序号，首次访问时的次序，以及探索完该顶点所有分支时的次序。边可以分成四种：树边，前向边，后向边（回边），横向边。(图片来自 算法概论 by dasgupta)

有向无环图和拓扑排序

• 有向图有环当且仅当DFS过程中遇到回边。
• 有向无环图中每一条边都指向一个finish值更小的顶点。
• 对于DFS，无环性、可线性化、无回边三者是等价的。

拓扑排序的两种方式:(1)由上述性质2可知，将顶点按照finish值降序排列即可。(2)每次删除一个只有出边没有入边的顶点。在实现时，记录下每个顶点的入边数量，一旦某个顶点的入边数量降为0，即可输出该顶点。这样的话两种算法的效率是一样的，都是O(V+E)。

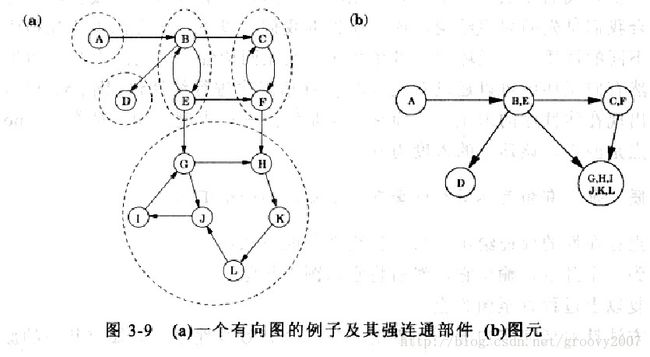
强连通分量

一个强连通分量是指分量中任意顶点之间都是互相可达的。将一个分量收缩成一个点，则原图变成一个有向无环图。(图片来自 算法概论 by dasgupta)

假设分量A有指向分量B的边，则从A做DFS一定可以探索完B的节点，而从B出发不可能到达任何A的节点。假设在收缩图中，B是一个汇点，那么从B的任何顶点出发，将只可能探索到B中的顶点。如何找到这样的汇点分量B呢？将原图的所有边反转，在收缩图中B就成为源点(只有出边没有入边)，就可以成为拓扑排序的第一个元素。算法实现：两遍DFS，先在原图上进行，然后在反转图上进行，且按照第一遍finish值递减的顺序，森林中的每一棵树就是一个分量。第一遍DFS的目的： If we do a DFS of graph and store vertices according to their finish times, we make sure that the finish time of a vertex that connects to other SCCs, will always be greater than finish time of vertices in the other SCC。实际上是为了对强连通分量做拓扑排序。代码实现 Strongly Connected Components

另一种思路来自《算法设计指南》by Skiena，DFS每找到一个环，就将环收缩成一个点，最后剩几个点就是几个强连通分量。这样就只需要一次DFS，参考书中代码实现。

关节点与桥

算法导论正文里未涉及本部分内容。关节点可以参考《算法设计指南》by Skiena。关节点(articulation point)：无向图中，删除之后变得不连通的点。桥：无向图中，删除之后变得不连通的边。找出一个图中所有的关节点和桥，都可以通过DFS。记住，无向图中只有树边和回边。

什么样的点能成为关节点，以下任意一种即可，注意第一种必须是root，第二种必须不是root，想想为什么：

 

• u is root of DFS tree and it has at least two children.
• u is not root of DFS tree and it has a child v such that no vertex in subtree rooted with v has a back edge to one of the ancestors (in DFS tree) of u.

 

代码及讲解 Articulation Points (or Cut Vertices) in a Graph，Bridges in a graph。这两篇文章都在geeksforgeeks网站上，文章后面附带了很多参考资料，并且代码可以在线修改和运行，非常适合学习。与之相关的一个概念，双连通分量，也可以通过类似的方法求解。

习题

习题编号以第3版为准

#22.1-6 线性时间的邻接矩阵算法

请给出O(V)的算法来判断有向图是否存在一个通用汇点（universal sink），即入度为|v|-1且出度为0的顶点。

解：参考instructor's manual，即存在某一行全部是0，且某一列全部是1（除了那一行）。对于i != j，若a[i,j]=0则顶点 j不可能是汇点，若a[i,j]=1则顶点i不可能是汇点，总之一次可以排除一个顶点。

#22.2-6 反例

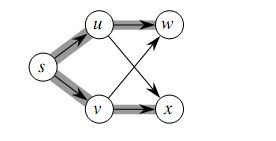
举例说明，在有向图G=(V,E)中，源顶点s，且树边集合E'满足对每一顶点v图(V,E')中从s到v的唯一路径是G中的一条最短路径；然而，不论在每个邻接表中各顶点如何排列，都不能通过在G上运行BFS而产生边集E'。

解：如图，图片来自instructor's manual

#22.2-8 树的直径

树的任意两个节点之间的最短路径的最大值称为树的直径，给出有效方法计算书的直径。

解：假设树为二叉树，最长路径要么在左子树中，要么在右子树中，要么从左子树最深的叶子上升到根，然后下降到右子树最深的叶子。T(n)=2T(n/2)+O(1)，时间复杂度O(n)。

实现方法1：宽度优先搜索，先从根节点进行BFS找到距离根最远的节点，然后从这个节点再进行一遍BFS。http://blog.csdn.net/harry_lyc/article/details/8197994

实现方法2：在深度优先搜索时，记录每个节点的高度（在探索完该节点的所有分支之后标记），根据节点u的子节点的高度就可以算出以u为根的子树的直径。

#22.2-9 无向图正反遍历

O(V+E)的时间找出无向图的一条路径，使得该路径恰好通过每条边两次，且两次方向相反。

解：本题是在BFS一节，与求欧拉回路的算法类似，答案见这里http://blog.csdn.net/wdq347/article/details/10265199

#22.3-8 反例

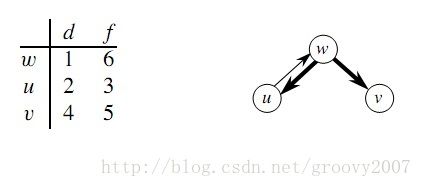
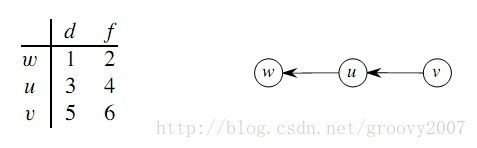
如果有向图存在一条从u到v的路径，并且在DFS时有u.discover < v.discover，则v是u在深度优先森林中的后代。请举出反例。

#22.3-9 反例

如果有向图存在一条从u到v的路径，则任何DFS都有u.finish >= v.discover。请举出反例。

解：这两道题的答案如图，图片来自instructor's manual

#22.3-11 森林中的唯一节点

有向图中的节点u如何能够成为深度优先森林中唯一的节点，即使u同时有出边和入边。

解：如图，图片来自instructor's manual

#22.3-13 单连通图

有向图G，任意两个节点之间最多只存在一条简单路径，则G是单连通图(singly connected)。请给出有效算法判断G是否单连通图。

解：参考http://blog.csdn.net/wdq347/article/details/11096945 主要思想：从每个点作一次DFS，得到一棵DFS树，如果没有出现DFS树内cross edge和forward edge，则此图必为单连通图。

#22.4-2 有向无环图中的简单路径数量

计算有向无环图中，两个节点s和v之间的路径的数量。

解：先拓扑排序，然后动态规划，类似于习题15-1有向无环图中的最长简单路径，以及课本24.2节“有向无环图中的单源最短路径问题”的算法。

#22.5-7 半连通图

有向图G，如果任意两个节点u和v，都存在u到v的路径或v到u的路径，则称为半连通的。请给出有效算法判断G是否半连通的。

解：错误的想法：如果对应的无向图是连通的，则G是半连通的，反例如下a <- b -> c，a和c之间就没有路径。正确的解法：参考instructor's manual，先求出强连通分量，做出收缩子图，只有收缩图是线形的时候，如a->b->c->d，G才是半连通的。

#22-2 无向图的衔接点、桥

解：https://www.byvoid.com/blog/biconnect，http://www.cppblog.com/myjfm/archive/2012/08/18/187617.html

#22-4 可到达性

解：见instructor's manual，思路是将所有边反转，然后按编号从小到大的顺序DFS，每一棵树的树根就是该树所有子节点能到达的最小节点。