Android游戏开发之连连看算法

因为有朋友在站内信中问到连连看的具体算法，所以我就把算法post出来，这个算法也是参考网上Flash游戏的算法改写的，原来的参考信息已经找不到了，不过非常感谢那些无私的朋友。

 

改写的连连看算法如下：

前置条件：用一二维数组存放Map,-1表示没有图案可以连通，非-1表示不同的图案。

首先是横向检测：

 

	private boolean horizon(Point a, Point b)
	    {
	        if(a.x == b.x && a.y == b.y)//如果点击的是同一个图案，直接返回false
	            return false;
	        int x_start = a.y <= b.y ? a.y : b.y;
	        int x_end = a.y <= b.y ? b.y : a.y;
	        for(int x = x_start + 1; x < x_end; x++)//只要一个不是-1，直接返回false
	            if(map[a.x][x] != -1){
	                return false;
	            }
	        return true;
	    }

 其次是纵向检测：

 

    private boolean vertical(Point a, Point b)
    {
        if(a.x == b.x && a.y == b.y)
            return false;
        int y_start = a.x <= b.x ? a.x : b.x;
        int y_end = a.x <= b.x ? b.x : a.x;
        for(int y = y_start + 1; y < y_end; y++)
            if(map[y][a.y] != -1)
                return false;
        return true;
    }

 一个拐角的检测：

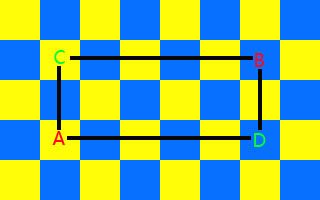
如果一个拐角能连通的话，则必须存在C、D两点。其中C点的横坐标和A相同，纵坐标与B相同，D的横坐标与B相同，纵坐标与A相同。

 

    private boolean oneCorner(Point a, Point b)
    {
        Point c = new Point(a.x, b.y);
        Point d = new Point(b.x, a.y);
        if(map[c.x][c.y] == -1)
        {
            boolean method1 = horizon(a, c) && vertical(b, c);
                return method1;
        }
        if(map[d.x][d.y] == -1)
        {
            boolean method2 = vertical(a, d) && horizon(b, d);
            return method2;
        } else
        {
            return false;
        }
    }

 两个拐角的检测：

这个比较复杂，如果两个拐角能连通的话，则必须存在图中所示的连线，这些连线夹在A、B的横、纵坐标之间,这样的线就以下这个类存储，direct是线的方向，用0、1表示不同的方向

LIne类结构如下：

 

class Line
    {
        public Point a;
        public Point b;
        public int direct;

        public Line()
        {
        }

        public Line(int direct, Point a, Point b)
        {
            this.direct = direct;
            this.a = a;
            this.b = b;
        }
    }

 

从A、B点的横纵两个方向进行扫描，就是Scan函数做的事情，把合适的线用LinkList存起来。

 

	private LinkedList scan(Point a, Point b)
	    {
	        ll = new LinkedList();
	        //Point c = new Point(a.x, b.y);
	        //Point d = new Point(b.x, a.y);
	        for(int y = a.y; y >= 0; y--)
	            if(map[a.x][y] == -1 && map[b.x][y] == -1 && vertical(new Point(a.x, y), new Point(b.x, y)))
	                ll.add(new Line(0, new Point(a.x, y), new Point(b.x, y)));
	
	        for(int y = a.y; y < map.row; y++)
	            if(map[a.x][y] == -1 && map[b.x][y] == -1 && vertical(new Point(a.x, y), new Point(b.x, y)))
	                ll.add(new Line(0, new Point(a.x, y), new Point(b.x, y)));
	
	        for(int x = a.x; x >= 0; x--)
	            if(map[x][a.y] == -1 && map[x][b.y] == -1 && horizon(new Point(x, a.y), new Point(x, b.y)))
	                ll.add(new Line(1, new Point(x, a.y), new Point(x, b.y)));
	
	        for(int x = a.x; x < map.column; x++)
	            if(map[x][a.y] == -1 && map[x][b.y] == -1 && horizon(new Point(x, a.y), new Point(x, b.y)))
	                ll.add(new Line(1, new Point(x, a.y), new Point(x, b.y)));
	
	        return ll;
	  }

 最后是两个拐角的算法：

 取出LinkList里面的线，测试A与B到该线的两点是否连通。

    private boolean twoCorner(Point a, Point b)
    {
        ll = scan(a, b);
        if(ll.isEmpty())
            return false;
        for(int index = 0; index < ll.size(); index++){
            Line line = (Line)ll.get(index);
            if(line.direct == 1){
                if(vertical(a, line.a) && vertical(b, line.b)){
                    return true;
                }

            } else
            if(horizon(a, line.a) && horizon(b, line.b)){
                return true;
            }
        }
        return false;
    }

 前面的函数有以下这个总的调用函数来调用，传入两个点，就可以判断这两个点是否符合连连看的算法了：

	public boolean checkLink(Point a,Point b){
		if(map[a.x][a.y] != map[b.x][b.y])//如果图案不同，直接为false
            return false;
        if(a.x == b.x && horizon(a, b))
            return true;
        if(a.y == b.y && vertical(a, b))
            return true;
        if(oneCorner(a, b))
            return true;
        else
            return twoCorner(a, b);
	}