有限域算数运算

椭圆曲线系统常采用算数运算操作执行一系列加解密操作，掌握有限域的算数运算方法，对设计高效执行的密码学算法至关重要。本文介绍了有限域的基本概念，进一步阐述了椭圆曲线系统的三种经典有限域（质数域，二元域和扩展域）以及其相应的算数运算方法(加法，减法，乘法和求逆运算)。

有限域介绍

数据域是相似数据系统（如有理数，实数和复杂数）及其属性的抽象概念。数据域可构成数据集合$F$，并执行两类基本运算：加法和乘法，一般满足如下性质：
（1）$(F,+)$是一个阿贝尔群，具有（加法）单位元0；
（2）$(F\backslash \{0\},\cdot )$是一个阿贝尔群，具有（乘法）单位元1；
（3）分配律：对所有 $a,b,c\in F$，满足：
$(a+b)\cdot c=a\cdot c+b\cdot c$。
如果集合$F$是有限的， 数据域也是有限的，称$F$为有限域。

数据域操作

如上节所述，数据域$F$具有两种类型操作，加法和乘法。依此类推，域元素的减法可按照加法定义，即对于$a,b\in F$, $a-b=a+(-b)$，其中$-b$在有限域$F$中唯一，且满足$b+(-b)=0$，则$-b$称为b的负数。相应的，数据域的除法可按照乘法定义，即对于$a,b\in F$,且$b\ne 0$，满足$a/b=a\cdot b^{-1}$，其中$b^{-1}$在有限域$F$中唯一， 且满足$b\cdot b^{-1}=1$，则称$b^{-1}是b的逆元$。

存在性和唯一性

在有限域中，阶指有限域的元素数量。称有限域F具有阶q，当且仅当q可以表示为质数的指数形式，也就是 $q=p^m$，其中质数p称为F的特征，m是正整数。如果$m=1$,称$F$为质数域。如果$m\ge 2$，称$F$为扩展域。对具有任意质数幂的阶q，仅仅存在一个有限域。 也就是说，任意两个具有相同阶q的有限域，尽管形式上其标识有可能不同，但却具有相同在形态。基于该性质，称任2个具有相同阶（假设阶为q）的有限域具有同态性，其同态域表示为$F_q$。

质数域

设p为质数，对整数取模p，就生成一个由元素$0,1,2,...,p-1$构成的整数集合，这个集合构成阶为p的有限域，表示为$F_p$，其中p为$F_p$的模数。对任意整数a，$a\mathrm{m}\mathrm{o}\mathrm{d}p$ 应表示余数r，且取值唯一，满足$0\le r\le p-1$。这个运算与$a/p$等价，也称为约化模$p$。

举个栗子，有限域$F_{29}$的元素集合为{0，1，2，…，28}。以下为一些算数运算的例子：
1 加法： $17+20=8$ ，因为 $37\mathrm{m}\mathrm{o}\mathrm{d}29=8$
2 减法： $17-20=26$，因为 $-3\mathrm{m}\mathrm{o}\mathrm{d}29=26$
3 乘法： $17\cdot 20=21$，因为 $340\mathrm{m}\mathrm{o}\mathrm{d}29=21$
4 求逆： $17^{-1}=12$，因为 $17\cdot 12\mathrm{m}\mathrm{o}\mathrm{d}29=1$

二元域

阶为$2^m$的有限域称为二元域或特征为2的有限域。一种构造$F_{2^m}$的方式是采用多项式的基本表示方法。以下是有域$F_{2^m}$表示为二元多项式的例子（多项式的系数在数据域$F_2=0,1$中），其度不超过为m-1。

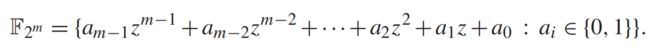
我们选取一个具有项数m的不可约的二元多项式$f(z)$（对任意m，这个多项式都是存在的）。$f(z)$具有的不可约性意味着$f(z)$不能被分解为（小于m）次幂的二元多项式的乘积。多项式系数值通常表示为的多项式加法后，对结果用2取模；多项式系数的乘法表示为执行约化多项式（reduction polynomial）$f(z)$的模。对任意二元多项式$a(z)$，$a(z)\mathrm{m}\mathrm{o}\mathrm{d}f(z)$表示执行$a(z)$除以$f(z)$的幂小于m的余数多项式$r(z)$，这个操作称为约化模$f(z)$。

例1（二元域$F_{2^4}$） 二元域$F_{2^4}$的元素表示为如下16个二元多项式，它的幂不超过3:

例2： 通过一个栗子说明在二元域$F_{2^4}$中如何用多项式$f(z)=x^4+z+1$进行一系列约化模运算。
1 加法：$(z^3+z^2+1)+(z^2+z+1)=z^3+z$
2 减法：$(z^3+z^2+1)-(z^2+z+1)=z^3+z$。
注意 $-1=1\mathrm{m}\mathrm{o}\mathrm{d}2$，一般的，对于任意$a\in F_{a^m}$，$-a=a\mathrm{m}\mathrm{o}\mathrm{d}2$
3 乘法：$(z^3+z^2+1)\dot{(}{z}^2+z+1)=z^2+1$，因为：$(z^3+z^2+1)\dot{(}{z}^2+z+1)=z^5+z+1$ 且$(z^5+z+1)\mathrm{m}\mathrm{o}\mathrm{d}(z^4+z+1)=z^2+1$.
4 求逆：$(z^3+z^2+1{)}^{-1}=z^2$，因为$(z^3+z^2+1)\cdot z^2\mathrm{m}\mathrm{o}\mathrm{d}(z^4+z+1)=1$

例3（同态域）：假设有3个幂为4的不可约二元多项式，分别为：$f_1(z)=z^4+z+1$，$f_2(z)=z^4+z^3+1$和$f_3(z)=z^4+z^3+z+1$。每个约化多项式能被用于构造域$F_2^4$；假设目标域分别为$k_1$,$k_2$,$k_3$。因此$k_1$,$k_2$,$k_3$的域元素同为16个二元多项式，其幂不超过3。换句话说，虽然这些域看起来明显不同，例如：在$k_1$中，$z^3.z=z+1$;在$k_2$中，$z^3.z=z^3+1$;在$k_3$中，$z^3.z=z^3+z^2+z+1$，但是它们具有相同的阶数，因此是同态的，只是元素具有不同的标记。K1和k2之间的同构性可以通过找到$c\in k_2$，c满足$f_1(c)\equiv 0\mathrm{m}\mathrm{o}\mathrm{d}{f}_2$，然后扩展$z⟼c$到同态$\phi :k_1\to k_2$来构造。 对c的选择可以为$z^2+z$,$z^2+z+1$,$z^3+z^2$和$z^3+z^2+1$。

扩展域

在二元域中，多项式可以泛化为如下扩展域形式。

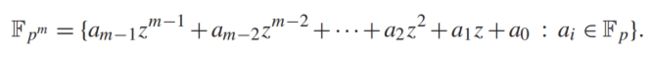
设p为质数，$m\ge 2$，$F_p[z]$表示以z为自变量，系数属于$F_p$的一元多次方程。设$f(z)$为一个幂为m（$m\in F_p[z]$）的不可约多项式，可以证明，该多项式对任意p和m是存在的。$f(z)$的不可约性意味着$f(z)$不能分解为$f(z)$中的多项式的乘积。在$F_{p^m}$中，元素是$F_p[z]$的多项式，且幂不大于m-1。
域元素的加法通常表示为多项式的和，其系数运算在$F_p$中执行。域元素的乘法表示为多项式$f(z)$的模。

例4（扩展域） 设p=251，m=5，$f(z)=z^5+z^4+12z^3+9^2+7$是$F_{251}[z]$中的不可约多项式，将$F_{251^5}$设为约化多项式，可知$F_{251}[z]$的阶为$251^5$，且$F_{251^5}$的元素为$F_{251}[z]$中的多项式，幂不大于4。
以下是有限域$F_{251^5}$中的算数运算，其中，$a=123z^4+76z^2+7z+4$，$b=196z^4+12z^3+225z^2+76$。
1 加法: $a+b=68z^4+12z^3+50z^2+7z+179$
2 减法： $a-b=178z^4+239z^3+102z^2+z^z+179$
3 乘法： $a\cdot b=117z^4+151z^3+117z^2+182z+217$
4 除法： $a^{-1}=109z^4+111z^3+250z^2+98z+85$

有限子域

当$k$是一个关于有限域$K$操作的数据域时，$K$的子集$k$即为$K$的子域，$K$称为$k$的一个扩展域。有限子域较为容易地特征化。设$F_{p^m}$是一个有限域，对于m的每个正除数$l$，都具有一个阶为$p^l$的子域，其元素满足$a^{p^l}=a$，且$a\in F_{p^m}$。反过来，对于一些m的正除数$l$，每个$F_{p^m}$的有限子域的阶为$p^l$。

有限域的基

$F_{q^n}$是一个建立在有限子域$F_q$基础上的向量空间。其中，空间中的向量是$F_{q^n}$的元素，其标量是$F_q$的元素，向量的和是$F_{q^n}$的加法运算，标量的乘积是$F_{q^n}$中$F_q$元素的乘法运算，向量空间是由不同基数构造的n维空间。
如果$B=b_1,b_2,...,b_n$表示一个基数，$a\in F_{q^n}$唯一表示为$F_q$元素的n元组$(a_1,a_2,...,a_n)$，其中$a=a_1{b}_1+a_2{b}_2+...+a_n{b}_n$。在以上有限域$F_{p^m}$的多项式基中，$F_{p^m}$是在$F_p$上的m维向量空间，$（z^{m-1},z^{m-2},...,z^2,z,1）$是建立在$F_p$上的$F_{p^m}$的基数。

有限域乘法群

有限域$F_q$的非0元素${F_q}^{\ast }$构成一个乘法循环群。此时元素$b(b\in {F_q}^{\ast })$存在，称为生成元。生成元满足以下关系式：${F_q}^{\ast }=\{b^i:0\le i\le q-2\}$。$a\in {F_q}^{\ast }$的阶是$a^t=1$的最小的正整数$t$。${F_q}^{\ast }$是一个循环群，且$t$为$q-1$的除数。