平衡树·splay

1.About splay

$splay$是实现平衡树的一种方法
他需要满足一个条件，就是对于一个点为根节点的子树，他的左子树全部小于根节点，右子树全部大于根节点
那他为什么叫这个名字呢？
我们查询一下百度翻译

但是事实上，感觉$splay$跟张开没什么关系…

可以说成展开树吧

$splay$的基本功能跟STL里面的$multiset$（$set$）比较像

他的思想的优秀之处在于，他每次都把操作完\要操作的点旋转到根节点并且保证满足他的性质，这样可以便于操作

2.基本操作

2.1 数组是干啥的？

在$splay$中我们要用到一些数组
fa[x]表示x的爸爸是谁
son[x][2]表示x的儿子分别是谁，son[x][0]表示他的左儿子，son[x][1]表示他的右儿子，把他的儿子们存到一个数组里是为了旋转的时候比较方便，我们后面说
siz[x]表示以x为根节点的子树的大小
key[x]表示x点上存的值
recy[x]表示值为key[x]的数出现了几次（我们把它存在一个点上）
tot表示这颗$splay$里面有几个不同的权值
rt表示根节点的位置

2.2 基本操作

clear操作
这个操作和下面要说的删除函数erase连用，用于彻底清除一个点的所有权值（因为这个点后面继续往里加值得时候可能还会用到）

其实非常的简单，把所有数组都设成0就可以了

inline void clear(int x){
	fa[x]=son[x][0]=son[x][1]=siz[x]=key[x]=recy[x]=0;
}

locate操作
这个操作和下面的$splay$的精华splay函数和rotate函数连用，用于判断一个点是他爸爸的左儿子还是右儿子

判断方法很简单，就是判断他爸爸的右儿子是不是他自己就可以了

inline bool locate(int x){
	return son[fa[x]][1]==x;	
}

update操作
当我们进行旋转或者更新之后，原来的点之间的数量关系就有可能发生变化，这时候我们需要进行更新，让每个节点对应的siz值是对的

inline void update(int x){
	if(x){
		siz[x]=recy[x];
		if(son[x][0])siz[x]+=siz[son[x][0]];
		if(son[x][1])siz[x]+=siz[son[x][1]];
	}
}

注意if(x)不能省

3.splay

3.1 rotate函数

rotate（旋转），用来将一个点向我们想要的地方（向上）移一层

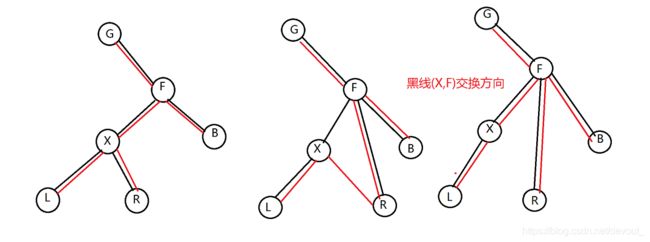
rotate分为左旋和右旋，下面以右旋为例

手画的好丑啊
我们想把X节点转到F的位置，我们不能单纯的把X转上去，因为这样会让X的度数变成4（G，L，R，F），不满足二叉树的性质了，所以我们必须要想一个办法。

我们发现，因为在左图中，R位于X的右子树，所以R应该比X大，所以当旋转完了之后，为了保证性质，所以R应该也在X的右子树，但是右子树已经被X曾经的爸爸给占了。但F的左子树不是还空着吗，就把R接到那里好了。

我们看左图，条件有L 也就是说，如果我们这样旋转，splay的性质并没有改变，所以左图和右图其实是等价的

所以这样旋转是合法的

当然左旋也差不多（可以想成F点从右图转到左图的过程）

当然，不要忘了update啊，X，F的关系都变了（特别是F原来是X的爸爸现在变成他儿子了），所以我们要update一下。

=========================
思想差不多就是那样，现在来简单说一下怎么把X旋上去

大家应该学过链表吧，我们在链表里想插入一个东西还挺麻烦的

这里的操作方法跟链表插入差不多，但是不同之处是所有点我们都知道他的编号，所以我们可以都存下来，然后就根本不用考虑顺序，瞎连就可以了

其中红线表示起点认终点为儿子，黑线表示终点认起点是爸爸

旋转完了之后的结果就是X之前的爸爸变成了自己的右儿子，自己之前都右儿子变成了自己的孙子，自己的爷爷变成了自己的爸爸，自己之前都兄弟变成了自己的孙子

inline void rotate(int x){
	int faz=fa[x],grand=fa[faz],side=locate(x);
	son[faz][side]=son[x][side^1],fa[son[faz][side]]=faz;//左右旋同时考虑
	son[x][side^1]=faz,fa[faz]=x;
	fa[x]=grand;
	if(grand)son[grand][son[grand][1]==faz]=x;//只有他有爷爷的时候才需要更新grand的儿子的情况
	update(faz),update(x);	//因为旋转后原来的faz跑到x下面了，所以要先更新faz
}

3.2 splay函数

我们学会了rotate，但是rotate只能向上转一层，我们要让他转到根节点，那怎么办呢？

我们用一个$splay$函数多次调用rotate来达到这一目的

但是我们需要分类讨论：

（声明洛谷版权）

为什么需要分类讨论呢？
我们看下面这张图可以更好的理解


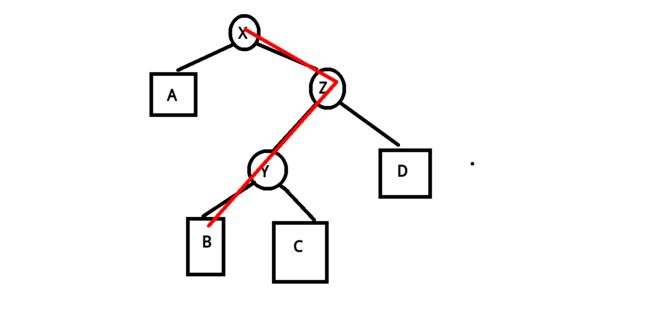
我们发现，如果我们对于x，y，都是左（右）儿子的情况，如果我们连转两次x的话，那么我们发现X-Y-Z-B的链是始终存在的，这样的话就容易被卡掉

inline void splay(int x){
	for(int faz;faz=fa[x];rotate(x))
		if(fa[faz])
			rotate(locate(x)==locate(faz)?faz:x);
	rt=x;
}

4.更新操作

4.1 插入函数

插入其实非常好理解（但是码量不小）

思路是这个样子的

1. 特判，如果树是空的就新加一个节点
2. 从根节点往下扫，每次走向该走的节点（因为满足splay的性质，所以如果插入的数x
3. 如果遇到一个点key[u]=x，那么把那个点的计数器recy+1，更新自己，更新爸爸，把自己转到根节点（方便操作）
4. 如果遇到一个点没有自己应该走的那个儿子，那就新加上一个点

看代码：

inline void insert(int x){
	if(!rt){//特判
		tot++;
		fa[tot]=son[tot][0]=son[tot][1]=0;
		siz[tot]=recy[tot]=1;
		key[tot]=x;
		rt=tot;
		return;
	}
	int u=rt,faz=0;
	while(1){
		if(key[u]==x){//如果有出现过的
			recy[u]++;
			update(u),update(faz);
			splay(u);
			return;
		}
		faz=u,u=son[u][x>key[u]];//选择走的方向
		if(!u){
			tot++;
			son[tot][0]=son[tot][1]=0;
			siz[tot]=recy[tot]=1;
			son[faz][x>key[faz]]=tot;
			fa[tot]=faz;
			key[tot]=x;
			update(faz);
			splay(tot);
			return;	
		}
	}
}

4.2 删除函数

查找函数
想要删除一个数，你要先找到他，所以删除的思路就是，先找到他，然后把它转到根节点，然后各种分类讨论（下面说）

怎么查找呢？跟插入差不多

如果x 如果x>key[u]，就往右走
如果x=key[u]，就停下来

inline void find(int x){
	int u=rt;
	if(!u)return;
	while(son[u][x>key[u]]&&key[u]!=x)u=son[u][x>key[u]];
	splay(u);//记得转，要不然白找了
}

查找最大的小于根节点的数
这个其实很简单，因为他是满足性质的，所以那个数一定在根节点的左子树的右子树的右子树的右子树的右子树…

找最小的大于根节点的数其实同理

inline int pre(){
	int x=son[rt][0];
	while(son[x][1])x=son[x][1];
	return x;	
}

inline int next(){
	int x=son[rt][1];
	while(son[x][0])x=son[x][0];
	return x;	
}

删除

找到了之后我们就可以删了，删除要分五类情况讨论：

1. 如果这个数出现了不止一次，即recy[rt]>1，则recy[rt]–，更新rt
2. 如果这个数既没有左子树也没有右子树（整棵树只有一个点），则直接clear这个点，rt=0
3. 如果这个数只有右子树，把根给自己的右儿子，清空原来的rt
4. 如果这个数只有左子树，同理
5. 我们找到最大的比要删除的数（根节点）大的数，把他转到根节点，这个时候我们要删的点就到根节点的右儿子的位置上了，连接一下根节点和要删除的点的右儿子就可以了

inline void erase(int x){
	rank(x);
	if(recy[rt]>1){
		recy[rt]--;
		update(rt);
		return;	
	}
	if(!son[rt][0]&&!son[rt][1]){
		clear(rt);
		rt=0;
		return;	
	}
	if(!son[rt][0]){
		int old=rt;
		rt=son[rt][1];
		fa[rt]=0;
		clear(old);
		return;
	}
	if(!son[rt][1]){
		int old=rt;
		rt=son[rt][0];
		fa[rt]=0;
		clear(old);
		return;	
	}
	int old=rt,lft=pre();
	splay(lft);
	son[rt][1]=son[old][1];
	fa[son[old][1]]=rt;
	clear(old);
	update(rt);
}

5.查询操作

5.1 查询一个数的排名(rank函数）

这个操作其实也不难，我们从根节点往下扫，开一个计数器res

如果x 否则将计数器加上siz[左儿子]（因为他左儿子的数肯定都比他小）
当遇到一个点他的key等于x，返回res+1
如果不相等，计数器加上recy[u]，往右儿子走

inline int rank(int x){
	int u=rt,res=0;
	while(1){
		if(x<key[u])u=son[u][0];
		else{
			res+=siz[son[u][0]];
			if(x==key[u]){
				splay(u);//可以不转，但是转了的话后面可以省事（不用写find）
				return res+1;
			}
			res+=recy[u];
			u=son[u][1];
		}
	}
}

5.2 查询第k大(kth函数）

这个跟上一个其实差不多

如果有左儿子并且k没有左儿子的数量多，往左儿子走
否则
计算一下如果第k大是当前节点的话k最多是多少（左儿子大小+当前节点recy），如果k小于那个值，返回当前节点的值
如果不小于，k减去那个值，往右儿子走

inline int kth(int x){
	int u=rt;
	while(1){
		if(son[u][0]&&x<=siz[son[u][0]])u=son[u][0];
		else{
			int sum=siz[son[u][0]]+recy[u];
			if(x<=sum)return key[u];
			u=son[u][1];
			x-=sum;	
		}
	}
}

5.3 查找一个数的前驱(lower)

怎么做呢？其实很简单，首先把那个数插进去，跑一下4.2里面说到的最大的小于根节点的数，就是他的前驱，然后再删掉那个点就可以了

inline int lower(int x){
	insert(x);
	int res=key[pre()];
	erase(x);
	return res;	
}

5.4 查找一个数的后继(upper)

跟5.3差不多，也是先插进去，调用next()函数，然后再删掉

inline int upper(int x){
	insert(x);
	int res=key[next()];
	erase(x);
	return res;	
}

6. 模板题代码

# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
# include 
using namespace std;

# define Rep(i,a,b) for(int i=a;i<=b;i++)
# define _Rep(i,a,b) for(int i=a;i>=b;i--)
# define RepG(i,u) for(int i=head[u];~i;i=e[i].next)

typedef long long ll;
const int N=1e5+5;
const int inf=0x7fffffff;
const double eps=1e-7;
template <typename T> void read(T &x){
	x=0;int f=1;
	char c=getchar();
	for(;!isdigit(c);c=getchar())if(c=='-')f=-1;
	for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+c-'0';
	x*=f;
}

int n;
int fa[N],son[N][2],siz[N],key[N],recy[N];
int rt,tot;

inline void clear(int x){
	fa[x]=son[x][0]=son[x][1]=siz[x]=key[x]=recy[x]=0;
}

inline bool locate(int x){
	return son[fa[x]][1]==x;	
}

inline void update(int x){
	if(x){
		siz[x]=recy[x];
		if(son[x][0])siz[x]+=siz[son[x][0]];
		if(son[x][1])siz[x]+=siz[son[x][1]];
	}
}

inline void rotate(int x){
	int faz=fa[x],grand=fa[faz],side=locate(x);
	son[faz][side]=son[x][side^1],fa[son[faz][side]]=faz;
	son[x][side^1]=faz,fa[faz]=x;
	fa[x]=grand;
	if(grand)son[grand][son[grand][1]==faz]=x;
	update(faz),update(x);	
}

inline void splay(int x){
	for(int faz;faz=fa[x];rotate(x))
		if(fa[faz])
			rotate(locate(x)==locate(faz)?faz:x);
	rt=x;
}

inline int pre(){
	int x=son[rt][0];
	while(son[x][1])x=son[x][1];
	return x;	
}

inline int next(){
	int x=son[rt][1];
	while(son[x][0])x=son[x][0];
	return x;	
}

inline int rank(int x){
	int u=rt,res=0;
	while(1){
		if(x<key[u])u=son[u][0];
		else{
			res+=siz[son[u][0]];
			if(x==key[u]){
				splay(u);
				return res+1;
			}
			res+=recy[u];
			u=son[u][1];
		}
	}
}

inline int kth(int x){
	int u=rt;
	while(1){
		if(son[u][0]&&x<=siz[son[u][0]])u=son[u][0];
		else{
			int sum=siz[son[u][0]]+recy[u];
			if(x<=sum)return key[u];
			u=son[u][1];
			x-=sum;	
		}
	}
}

inline void insert(int x){
	if(!rt){
		tot++;
		fa[tot]=son[tot][0]=son[tot][1]=0;
		siz[tot]=recy[tot]=1;
		key[tot]=x;
		rt=tot;
		return;
	}
	int u=rt,faz=0;
	while(1){
		if(key[u]==x){
			recy[u]++;
			update(u),update(faz);
			splay(u);
			return;
		}
		faz=u,u=son[u][x>key[u]];
		if(!u){
			tot++;
			son[tot][0]=son[tot][1]=0;
			siz[tot]=recy[tot]=1;
			son[faz][x>key[faz]]=tot;
			fa[tot]=faz;
			key[tot]=x;
			update(faz);
			splay(tot);
			return;	
		}
	}
}

inline void erase(int x){
	rank(x);//这里偷了个懒，因为rank后面我们把那个点转上去了，所以我们这里就不用再专门的写find了
	if(recy[rt]>1){
		recy[rt]--;
		update(rt);
		return;	
	}
	if(!son[rt][0]&&!son[rt][1]){
		clear(rt);
		rt=0;
		return;	
	}
	if(!son[rt][0]){
		int old=rt;
		rt=son[rt][1];
		fa[rt]=0;
		clear(old);
		return;
	}
	if(!son[rt][1]){
		int old=rt;
		rt=son[rt][0];
		fa[rt]=0;
		clear(old);
		return;	
	}
	int old=rt,lft=pre();
	splay(lft);
	son[rt][1]=son[old][1];
	fa[son[old][1]]=rt;
	clear(old);
	update(rt);
}	

inline int lower(int x){
	insert(x);
	int res=key[pre()];
	erase(x);
	return res;	
}

inline int upper(int x){
	insert(x);
	int res=key[next()];
	erase(x);
	return res;	
}

int main()
{
	read(n);
	Rep(i,1,n){
		int opt,x;
		read(opt),read(x);
		switch(opt){
			case 1:insert(x);break;
			case 2:erase(x);break;
			case 3:printf("%d\n",rank(x));break;
			case 4:printf("%d\n",kth(x));break;
			case 5:printf("%d\n",lower(x));break;
			case 6:printf("%d\n",upper(x));break;
		}
	}
	return 0;
}

7. 写在最后

总算是写完了

$splay$作为码量最大的平衡树之一以及效率最低的平衡树之一，至少不用像$treap$一样靠脸吃饭吧…

by：一位只会splay的蒟蒻

素材来源：$luogu$博客，$yyb$的博客($orzyyb$)