矩阵(斐波那契数列和Strassen矩阵)下的分治算法及其分治算法的改进(上)
我昨天在想,应试教育真的会把知识学死吗。我认为这只是一个借口,教育本来就不是活的,如果我们不主动去思考,去应用。而只是一味的为了考试而去学习,当然会把知识学的没有用处。所以说不是应试教育把知识学死了,而是你把知识学死了。
《增广贤文》里面有一句老话是:师傅领进门,修行在个人。前辈将知识传给我们,我们是要在其上进行再提炼,发展到我们的当代生活中。所以才有我们现在的美好生活。文化这个东西是不断再传承的!
本篇会介绍快速幂算法的应用斐波那契数列,以及分治算法的改进途径。
1、O(1)究竟是个啥
我从百度上搜,实际上也只是说。O(1)就是一个其基本操作重复执行的次数是一个固定的常数,执行次数不存在变化,是一个常数阶。O(1)是个常数,并不是1。我昨天一直在想这个问题,我认为的O(1)只是判断啊,乘法那些的一个常数量。而1就是一条语句。
实际上没必要扣太多这些东西。上一篇快速幂是+O(1),那是因为里面有些乘法是固定的时间就能解出来的,就是不随n的量发生变化,而汉诺塔加的是1。那个1是个move的调用而已,加O(1)也是可以的,最后也是2^n。而且为什么有的时候明明是要有O(1)的计算量,为什么就忽略了呢。我认为啊,没写O(1)的,大部分是因为有比O(1)更大的量作为了上界,所以就没写。而且分治算法总要是有个常数的量的,不然判断那种代码不可能不花时间啊。不然纯递归也没有啥意义啊,你们觉得呢?
至于为什么开篇介绍这个,是因为昨天睡觉,一直对这些有疑问,想不明白,为什么汉诺塔你加个1,而快速幂是要加O(1)的,而且快速幂明明不是个二叉树,深度k没法计算啊。而且对于树的深度,某某数据结构上写的是从1开始。某某离散数学上又写从0开始。所以一直是个谜。
好了,开篇就说这么多,只是单纯的把昨天的疑问写了出来而已。下面进入正题
2、斐波那契数列及其优化
什么是斐波那契数列
指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*),像满足那样递推方程的为斐波那契数列。
斐波那契数列的算法
我觉得这个算法,在大学编程中是接触的最多的。因为在开发中,一旦说起了递归,第一印象就是斐波那契数列。所以算法很熟悉
例如,我们要求前20项斐波那契数列。
递归求斐波那契数列
我们先采用最熟悉的递归写法,对于斐波那契数列的递归写法,就是两点,第一点写通项(记住递归算法的设计,第一项都是先思考通项式,也就是递归式是什么,然后我们再思考出口在哪)
这个的通项就是上面的通项啊 就是return fib(n-1)+fib(n-2)。
然后思考出口,你传入的是n这个参数,我们思考边界,n=4,还是要进行递归得3和2,然后3进入递归是2和1。然后如果是1或者是2进入递归,总归有fib(0)出现了。0就没有意义了,所以我们防止fib(0)的出现,就不要让1或者是2进入递归,那么我们要为其设置出口。即if(n1||n2)return 1;(因为前两项都是1)
因此我们可以写代码
public static void main(String[] args) {
// TODO Auto-generated method stub
for(int i=1;i<=20;i++) {
int fib=fib(i);
System.out.print(fib+" ");
}
}
//递归求斐波那契数
public static int fib(int n) {
if(n==1||n==2)
return 1;
else
return fib(n-1)+fib(n-2);
}
对递归求斐波那契数列进行分析
这个是T(n)=T(n-1)+T(n-2)
这个递推方程怎么解,如果大家感兴趣,可以去百度百科上看看。这里就不在介绍了(嗯,我就是不会)。直接给出答案T(n)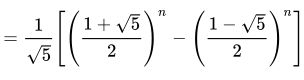
我们能清楚的看到,求出来的时间复杂度就是O(2^n)。也就是说斐波那契数列用递归写居然是一个指数级的量
为什么会出现一个指数级的量,我们看一个图
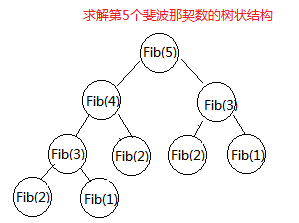
你看啊,我要求fib(5),那就得求fib(4)和fib(3),而求fib(4)就要求fib(3)和fib(2),而这个fib(3)求了两次,也就是这个东西被递归了两次。如果是更大的值,那么得有一半的数据递归了两遍,这样严重浪费时间。所以产生了这么庞大的时间复杂度
迭代求斐波那契数列
对于迭代求法,我相信有很多人对它陌生,这东西怎么用for循环实现
实际上很简单,首先这个f(n)是不是第前一个项和第前两个项的和啊。所以我们就用一个变量记录f(n-2),用另一个变量记录f(n-1)。而结果正是它们的和。
首先设result=1,pre=1,after=1
因为pre,after已经涵盖了前两项的值,而且此时返回result也是前两个的值。ok,那我们从第三项开始分析
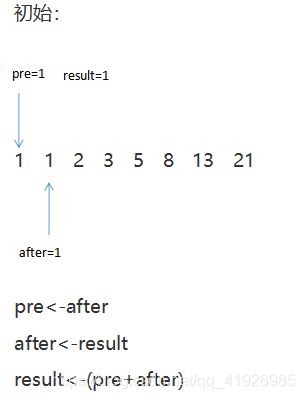



这个分析就不再多说了,还是一样的前两项直接输出result,第三项开始计算f(3),从i=3,到i=n。最后返回result,因此来编写代码
public static void main(String[] args) {
// TODO Auto-generated method stub
for(int i=1;i<=20;i++) {
int fib=fib2(i);
System.out.print(fib+" ");
}
}
//迭代求斐波那契数
public static int fib2(int n) {
int result=1; //得结果
int pre=1; //记录前两次计算的结果
int after=1; //记录前一个结果
for(int i=3;i<=n;i++) {
//假设计算f(n)
pre=after; //这个是f(n-2)
after=result; //这个是f(n-1)
result=pre+after;
}
return result;
}
迭代求斐波那契数列分析
这里从i=3到i<=n,总共n-2个数
即
T(n)=n-2 (n>2)
T(1)=T(2)=1
我们得出时间复杂度是O(n)。
迭代求斐波那契数列却是O(n),居然比递归还小。因为迭代不存在重复,所以说它相比递归来说时间上更有效率。
既然说快速幂的应用是用来求斐波那契数列。那么下面我们来看看,怎么用快速幂的形式来求解斐波那契数列
矩阵快速幂算法
我们可以将斐波那契数列的求解写成矩阵的形式,就像这样:
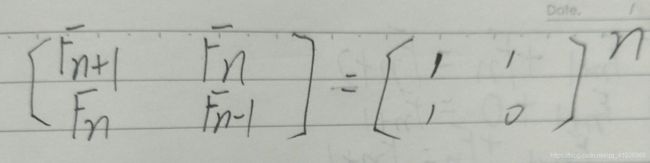
下面我们用数学归纳法进行证明:

关于矩阵乘法的东西,如果没有学过或者忘了线性代数的,可以百度或者看后面的介绍的矩阵乘法
矩阵乘法
矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有意义。
如何用代码实现,我们先想,矩阵是怎么表现的?大家学二维数组的时候已经明白过这个是可以用矩阵的对吧。所以就是用矩阵来表示。

对于代码实现,如果两个数组都告诉你了。我给你一个最简单的方法
public static void main(String[] args) {
// TODO Auto-generated method stub
int a[][]=new int[][] {{2,4},{5,6}};
for(int i=0;i<r.length;i++) {
for(int j=0;j<r[0].length;j++) {
System.out.print(r[i][j]+" ");
}
System.out.println();
}
}
//简单矩阵幂乘运算
public static int[][] multiple(int a[][],int b[][]) {
int r[][]=new int[a.length][b[0].length]; //相乘后的矩阵的大小是a的行,b的列
//进行8次乘法运算
r[0][0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
r[0][1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
r[1][0]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
r[1][1]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
return r;
}
这个我们通过矩阵乘法逻辑就可以写出这样的代码,看着很陋。实际上写出来,是用来分析,这个代码逻辑做了8次乘法,4次加法。可以用O(1)的量来评定。是吧。
好我们来分析矩阵乘法如何用代码迭代实现。
比如说A矩阵是一个i行j列,B矩阵是一个j行k列的矩阵。两个相乘
我们拿出一例来分析
c[0][0]=a[0][0]·b[0][0]+a[0][1]·b[1][0] 2行2列·2行3列
c[0][0]=a[0][0]·b[0][0]+a[0][1]·b[1][0]+a[0][2]·b[2][0] 2行3列·2行3列
我们可以看到,c[0][0]=a[0][j]·b[j][0]+c[0][0]
再看c[0][1]=a[0][0]·b[0][1]+a[0][1]·b[1][1] 2行2列·2行3列
c[0][1]=a[0][0]·b[0][1]+a[0][1]·b[1][1]+a[0][2]·b[2][1] 2行3列·2行3列
我们可以看到,c[0][1]=a[0][j]·b[j][1]+c[0][1]
我们用c[i][k]用来给数组赋值,让j作为中间变量进行计算
得出c[i][k]=a[i][j]*b[j][k]+c[i][k]
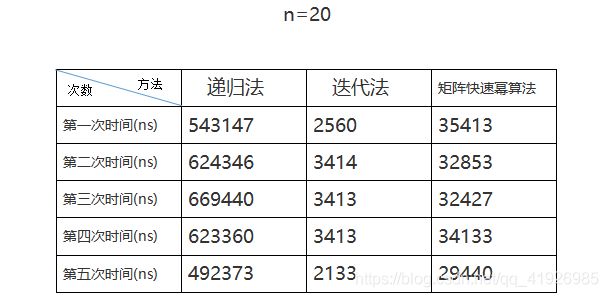
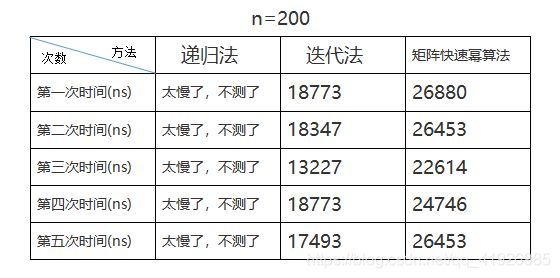
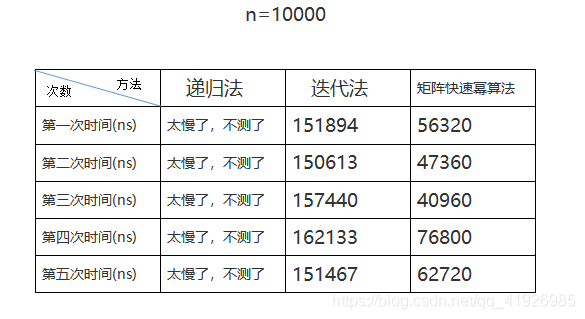
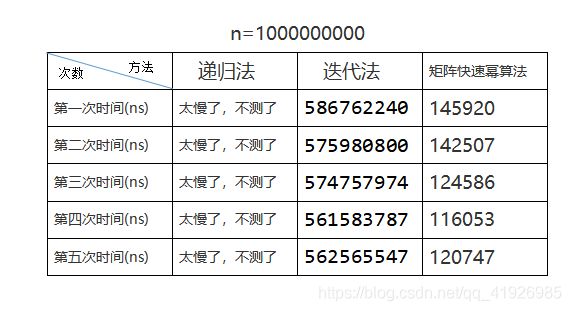
也就是说 通过这样分析时间复杂度是O(n^3) 因此我们可以写代码得 我们回到斐波那契数列的第三种求法 递归是T(n/2) 也许你会问,上面你说是矩阵迭代算法是O(n^3),而这里又是O(1)。实际上我们看啊。他们都是二阶矩阵二阶矩阵。然而二阶矩阵二阶矩阵,你看那个我说的最陋的写法,是不是就是8次乘法,4次加法就搞定了。 实际上虽然是迭代但是 所以说T(n)=T(n/2)+8·O(1) 这里我们把斐波那契数列的时间复杂度居然降到了O(logn)。但是你看啊,这个代码写的这么多,这儿算法真的就这么快吗? 下面我们进行时间测试 我们分别以上述三种方法进行测试,分别取第n=20,n=500,n=10000项,n=1000000000。测试5次,参考表如下: 大家看,对于n取很小的时候,迭代法效率快。而矩阵快速幂处理的乘法次数太多,所以没有迭代法快。而对于n取很大的时候,迭代法远不如矩阵快速幂,这是因为O(logn) 所以,算法处理的优化大部分就是对数据量很大的时候的优化。 分治算法的时间复杂度方程: 而当a比较大,b较小,f(n)不大时,方程的解是: 因此我们得出一个结论,减少a是降低函数T(n)的阶的途径,进而就能降低时间复杂度 我们可以利用子问题依赖关系,使某些子问题的解通过组合其他子问题的解而得到,也就是说,如果某些子问题存在依赖关系,我们可以把其他子问题的结果经过简单变换,运算就能得到那些子问题运算结果。这样就能降低子问题个数。 下面我们来看个例子: 下面我们来对这个例子的算法进行探讨 大家可能会想,直接用矩阵乘法算啊。然而这个n我们是不知道的。不能像上边那样算快速幂那样,知道n永远是2,从而得出二阶矩阵就是8次乘法,4次加法的。所以在n不知道的情况下。我们再想通过简单的幂乘运算去算,那就是O(n^3)。 那怎么办? 诶,刚才有说,两个n阶矩阵相乘中的8次乘法和4次加法是在阶数为2阶的时候得到的。那么能不能把这个两个n阶矩阵划分成n/2阶的矩阵,然后最后划分到2阶矩阵相乘呢。 好,我们用分治法来这样处理下。 我们看图 得说清楚,这个A11,B11啥的都是一个矩阵块。最后划分划分的,变成了这么一个2阶矩阵相乘。 下面我们来分析下这个分治算法 我们再举例子 我们将上面的二阶再拿出来举个例子 我们看到两个二阶相乘是4次加法,Addmetrix(Divideconquer(a1, b1, n),Divideconquer(a2, b3, n),n);这里参数是四个二阶矩阵两两相乘,故有8次加法 设c为常数 我们根据主定理 结果算了半天,时间复杂度还是和原始的解法一样。而且空间复杂度远大于原始的解法。而且代码复杂程度更远超原始解法。 至于分治法的代码,我就不分析了。基本的东西我已经在上边用图画出来了,整个过程思考思考就能写出来 伪码网上都有,一看就很简单。但是实际上要写出代码,真没这么简单。因为你要考虑如何划分矩阵。 你看上面的求法又复杂,又浪费时间。那有没有减少乘法次数(即减少子问题个数)你还别说,还真有。我都不知道这个大神是怎么想出来的 Strassen通过各种凑数,终于发现可以通过对划分的4个小矩阵进行7次变换,可以减少一次乘法操作。 采用中间结果,设定中间矩阵,将中间矩阵再组合就可以求出来了 因此我们分析得出递推方程 根据主定理得,T(n)=O(nlog7)=O(n2.8075) 我们看到这种算法居然比O(n^3)小。因此达到了一种优化。 编写这个代码,我们可以根据上边分治法的代码进行改进。代码如下: 然而n阶矩阵乘法优化还在不断探索中 矩阵算法在生活中特别有用,尤其是在数据挖掘和图像处理以及科学计算中用处很大 我们利用子问题依赖关系,用某些子问题解的代数表达式表示另一些子问题的解,减少独立计算子问题个数
i=0,ipublic static void main(String[] args) {
// TODO Auto-generated method stub
int a[][]=new int[][] {{2,4},{5,6}};
int b[][]=new int[][] {{1,3,9},{7,8,4}};
int r[][]=multiple2(a, b);
for(int i=0;i<r.length;i++) {
for(int j=0;j<r[0].length;j++) {
System.out.print(r[i][j]+" ");
}
System.out.println();
}
}
//迭代矩阵幂乘运算
public static int[][] multiple2(int a[][],int b[][]){
int r[][]=new int[a.length][b[0].length]; //相乘后的矩阵的大小是a的行,b的列
for(int i=0;i<a.length;i++) //i行j列*j行k列
for(int k=0;k<b[0].length;k++)
for(int j=0;j<b.length;j++)
r[i][k]=a[i][j]*b[j][k]+r[i][k];
return r;
}
也是一样是求幂乘运算,我们在快速幂的算法下进行矩阵快速幂算法。
这里就交给大家分析了,矩阵的迭代写法和快速幂算法已经讲过了。直接贴代码public static int matrix[][]; //定义斐波那契数列的矩阵
public static int Initial[][]=new int[][]{{1,1},{1,0}}; //定义初始值
public static void main(String[] args) {
// TODO Auto-generated method stub
for(int i=1;i<=20;i++) {
int fib[][]=fib3(i);
System.out.print(fib[0][1]+" ");
}
}
//优化斐波那契数的求法
public static int[][] fib3(int n) {
if(n==1)
return Initial;
else
matrix=fib3(n>>1);
if(n%2==0)
return Mutilple(matrix, matrix);
else
return Mutilple(Mutilple(matrix, matrix), Initial);
}
//矩阵快速幂求法
public static int[][] Mutilple(int a[][],int b[][]){
int r[][]=new int[a.length][b[0].length]; //相乘后的矩阵的大小是a的行,b的列
for(int i=0;i<a.length;i++) //i行j列*j行k列
for(int k=0;k<b[0].length;k++)
for(int j=0;j<b.length;j++)
r[i][k]=a[i][j]*b[j][k]+r[i][k];
return r;
}
矩阵快速幂算法分析
而矩阵快速幂算法是O(1)的量
i=0,i<2
j=0,j<2
k=0,k<2
这样看就只需要8次循环就行了,这个8不就是个常数,那时间复杂度不就是O(1),而我说的那个O(n^3),是不知道几阶*几阶啊。而且涵盖的是8次乘法,而且乘法是固定的算法吧,不随n的多少而发生变化吧。总不能n多了,你这个乘法就改变了,我们可以说乘法的次数增加了,但乘法本质的没有改变,而且乘法还是这里面耗性能最大的,所以说矩阵快速幂算法就是8·O(1)。
我们通过主定理解出算法的时间复杂度是O(logn)
3、改进分治算法的途径
减少子问题个数
T(n)=aT(n/b)+f(n)
我们看到,n/b是子问题规模,T(n/b)是这一类子问题的工作量,a是子问题个数,f(n)是划分与综合工作量。T(n)就是对规模是n的问题所做的基本运算次数
T(n)=Θ(n^logb a)
我们看到啊,如果我们把子问题个数降下来,这样我们就能看到n的指数就会下降,那么这个时间复杂度就降下来了。
对于矩阵运算,我们在上边已经晓得一些了。
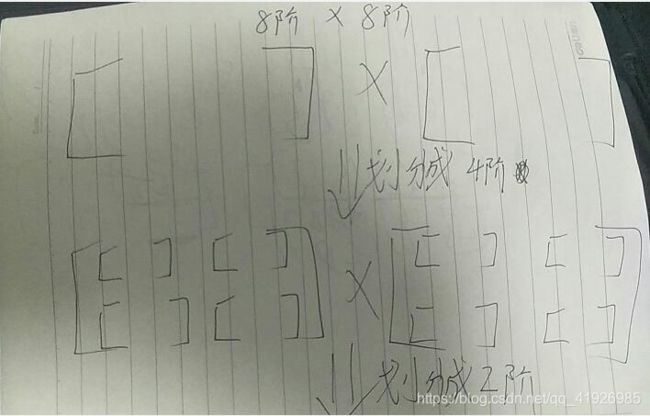
那么怎么求两个n阶矩阵的乘积(n=2^k)
我们假设n=2^k,将A,B,C划分成大小为(n/2)*(n/2)的子矩阵,然后我们有
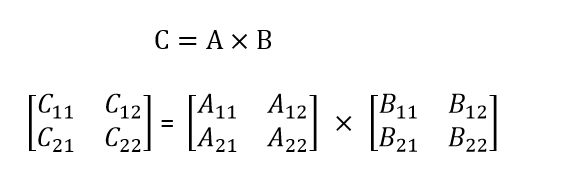
因此,我们有

你看每一个二阶矩阵是不是都是8次乘法和4次加法
然后我们递归都是n/2,所以是T(n/2)
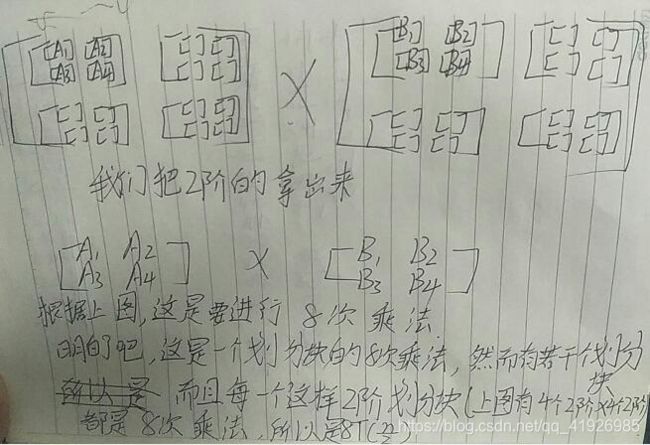
然后根据上图,我们做了8次乘法,记住这8次是一个二阶矩阵块的8次。不是所有的矩阵块,所有矩阵块的乘法次数是远远超过8次的。也许你会问什么意思?
这是求c1的式子
就这样求完c1,c2,c3,c4之后,合并成一个四阶矩阵
然后我们用上面的例子想想加法
同层次之间再进行1次加法(代码中的Addmetrix加法),而进入这个加法代码中还进行了n/2*n/2的循环,故我们用一个常数表示加法次数
因此列出递推方程T(n)=8T(n/2)+cn2
这里a=8,b=2,f(n)=cn2
n^((log2 8)-E),存在E=1使f(n)=O(n^((log2 8)-E)),则f(n)=Θ(n3)不想看代码直接跳过吧
public static void main(String[] args) {
// TODO Auto-generated method stub
int a[][]=new int[][] {{7,4,5,13,75,69,12,25},{6,3,5,7,36,58,96,24},{3,4,6,2,36,25,14,0},{9,5,4,1,25,14,8,9},{12,12,18,0,25,14,8,9},{36,58,47,2,25,14,8,9},{14,15,19,21,25,14,8,9},{36,21,0,0,25,14,8,9}};
int b[][]=new int[][] {{1,3,9,5,25,14,8,9},{7,8,4,10,25,14,8,9},{3,4,2,8,25,14,8,9},{1,10,0,6,25,14,8,9},{27,15,18,19,36,58,96,24},{36,25,41,0,36,58,96,24},{1,2,3,4,36,58,96,24},{8,56,78,2,36,58,96,24}};
int r[][]=Divideconquer(a, b, 8);
for(int i=0;i<r.length;i++) {
for(int j=0;j<r[0].length;j++) {
System.out.print(r[i][j]+" ");
}
System.out.println();
}
}
//迭代矩阵幂乘运算
public static int[][] multiple2(int a[][],int b[][]){
int r[][]=new int[a.length][b[0].length]; //相乘后的矩阵的大小是a的行,b的列
for(int i=0;i<a.length;i++) //i行j列*j行k列
for(int k=0;k<b[0].length;k++)
for(int j=0;j<b.length;j++)
r[i][k]=a[i][j]*b[j][k]+r[i][k];
return r;
}
//划分矩阵
public static int[][] Dividemetrix(int a[][],int n,int number){
int row=n>>1;
int cols=n>>1;
int r[][]=new int[row][cols];
switch(number) {
case 1:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i][j];
break;
case 2:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i][j+cols];
break;
case 3:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i+row][j];
break;
case 4:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i+row][j+cols];
break;
default :
break;
}
return r;
}
//矩阵求和
public static int[][] Addmetrix(int a[][],int b[][],int n){
int result[][]=new int[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
result[i][j]=a[i][j]+b[i][j];
return result;
}
//聚合矩阵
public static int[][] Togethermetrix(int a[][],int b[][],int c[][],int d[][],int n){
int result[][]=new int[n<<1][n<<1];
for(int i=0;i<n*2;i++)
for(int j=0;j<n*2;j++) {
if(i<n){
if(j<n){
result[i][j] = a[i][j];
}
else
result[i][j] = b[i][j-n];
}
else{
if(j<n){
result[i][j] = c[i-n][j];
}
else{
result[i][j] = d[i-n][j-n];
}
}
}
return result;
}
//分治法求解
public static int[][] Divideconquer(int a[][],int b[][],int n){
//定义接受结果的数组
int result[][]=new int[n][n];
//阶为2直接做乘法
if(n==2)
return multiple2(a, b);
else
{
//定义a数组,并划分成四块
int a1[][]=Dividemetrix(a,n,1);
int a2[][]=Dividemetrix(a,n,2);
int a3[][]=Dividemetrix(a,n,3);
int a4[][]=Dividemetrix(a,n,4);
//定义b数组,并划分成四块
int b1[][]=Dividemetrix(b, n, 1);
int b2[][]=Dividemetrix(b, n, 2);
int b3[][]=Dividemetrix(b, n, 3);
int b4[][]=Dividemetrix(b, n, 4);
//将接受结果的数组进行划分成四块
int result1[][]=Dividemetrix(result, n, 1);
int result2[][]=Dividemetrix(result, n, 2);
int result3[][]=Dividemetrix(result, n, 3);
int result4[][]=Dividemetrix(result, n, 4);
n=n>>1;
//递归划分出阶为2矩阵并将求出来的矩阵求和
result1=Addmetrix(Divideconquer(a1, b1, n),Divideconquer(a2, b3, n),n);
result2=Addmetrix(Divideconquer(a1, b2, n),Divideconquer(a2, b4, n),n);
result3=Addmetrix(Divideconquer(a3, b1, n),Divideconquer(a4, b3, n),n);
result4=Addmetrix(Divideconquer(a3, b2, n),Divideconquer(a4, b4, n),n);
//将解合并成2*n的矩阵
result=Togethermetrix(result1,result2,result3,result4,n);
}
return result;
}
Strassen矩阵


我们看到这里进行了7次乘法,18次加(减)法
T(n)=7(n/2)+18(n/2)2
T(1)=1public static void main(String[] args) {
// TODO Auto-generated method stub
int a[][]=new int[][] {{7,4,5,13,75,69,12,25},{6,3,5,7,36,58,96,24},{3,4,6,2,36,25,14,0},{9,5,4,1,25,14,8,9},{12,12,18,0,25,14,8,9},{36,58,47,2,25,14,8,9},{14,15,19,21,25,14,8,9},{36,21,0,0,25,14,8,9}};
int b[][]=new int[][] {{1,3,9,5,25,14,8,9},{7,8,4,10,25,14,8,9},{3,4,2,8,25,14,8,9},{1,10,0,6,25,14,8,9},{27,15,18,19,36,58,96,24},{36,25,41,0,36,58,96,24},{1,2,3,4,36,58,96,24},{8,56,78,2,36,58,96,24}};
int r[][]=Strassen(a, b, 8);
for(int i=0;i<r.length;i++) {
for(int j=0;j<r[0].length;j++) {
System.out.print(r[i][j]+" ");
}
System.out.println();
}
}
//划分矩阵
public static int[][] Dividemetrix(int a[][],int n,int number){
int row=n>>1;
int cols=n>>1;
int r[][]=new int[row][cols];
switch(number) {
case 1:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i][j];
break;
case 2:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i][j+cols];
break;
case 3:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i+row][j];
break;
case 4:
for(int i=0;i<row;i++)
for(int j=0;j<cols;j++)
r[i][j]=a[i+row][j+cols];
break;
default :
break;
}
return r;
}
//矩阵求和
public static int[][] Addmetrix(int a[][],int b[][],int n){
int result[][]=new int[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
result[i][j]=a[i][j]+b[i][j];
return result;
}
//矩阵乘法
public static int[][] Multiple3(int a[][],int b[][],int n){
int m1,m2,m3,m4,m5,m6,m7;
int result[][]=new int[n][n];
m1=a[0][0]*(b[0][1]-b[1][1]);
m2=b[1][1]*(a[0][0]+a[0][1]);
m3=b[0][0]*(a[1][0]+a[1][1]);
m4=a[1][1]*(b[1][0]-b[0][0]);
m5=(a[0][0]+a[1][1])*(b[0][0]+b[1][1]);
m6=(a[0][1]-a[1][1])*(b[1][0]+b[1][1]);
m7=(a[0][0]-a[1][0])*(b[0][0]+b[0][1]);
result[0][0]=m5+m4-m2+m6;
result[0][1]=m1+m2;
result[1][0]=m3+m4;
result[1][1]=m5+m1-m3-m7;
return result;
}
//矩阵减法
public static int[][] Matrixminus(int a[][],int b[][],int n){
int result[][]=new int[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
result[i][j]=a[i][j]-b[i][j];
return result;
}
//聚合矩阵
public static int[][] Togethermetrix(int a[][],int b[][],int c[][],int d[][],int n){
int result[][]=new int[n<<1][n<<1];
for(int i=0;i<n*2;i++)
for(int j=0;j<n*2;j++) {
if(i<n){
if(j<n){
result[i][j] = a[i][j];
}
else
result[i][j] = b[i][j-n];
}
else{
if(j<n){
result[i][j] = c[i-n][j];
}
else{
result[i][j] = d[i-n][j-n];
}
}
}
return result;
}
//Strassen矩阵
public static int[][] Strassen(int a[][],int b[][],int n){
int result[][]=new int[n][n];
if(n==2) //当两个矩阵都是二阶时,则计算乘法
return Multiple3(a, b, n);
else
{
int a1[][]=Dividemetrix(a,n,1);
int a2[][]=Dividemetrix(a,n,2);
int a3[][]=Dividemetrix(a,n,3);
int a4[][]=Dividemetrix(a,n,4);
int b1[][]=Dividemetrix(b, n, 1);
int b2[][]=Dividemetrix(b, n, 2);
int b3[][]=Dividemetrix(b, n, 3);
int b4[][]=Dividemetrix(b, n, 4);
int result1[][]=Dividemetrix(result, n, 1);
int result2[][]=Dividemetrix(result, n, 2);
int result3[][]=Dividemetrix(result, n, 3);
int result4[][]=Dividemetrix(result, n, 4);
n=n>>1;
int m1[][]=new int[n][n];
int m2[][]=new int[n][n];
int m3[][]=new int[n][n];
int m4[][]=new int[n][n];
int m5[][]=new int[n][n];
int m6[][]=new int[n][n];
int m7[][]=new int[n][n];
m1=Strassen(a1, Matrixminus(b2, b4, n), n);
m2=Strassen(Addmetrix(a1, a2, n), b4, n);
m3=Strassen(Addmetrix(a3, a4, n), b1, n);
m4=Strassen(a4, Matrixminus(b3, b1, n), n);
m5=Strassen(Addmetrix(a1, a4, n), Addmetrix(b1, b4, n), n);
m6=Strassen(Matrixminus(a2, a4, n), Addmetrix(b3, b4, n), n);
m7=Strassen(Matrixminus(a1, a3, n), Addmetrix(b1, b2, n), n);
result1=Addmetrix(Matrixminus(Addmetrix(m5, m4, n), m2, n), m6, n);
result2=Addmetrix(m1, m2, n);
result3=Addmetrix(m3, m4, n);
result4=Matrixminus(Matrixminus(Addmetrix(m5, m1, n), m3, n), m7, n);
result=Togethermetrix(result1,result2,result3,result4,n);
return result;
}
}
Coppersmith-Winograd算法将矩阵乘法降到了O(n^2.376)
这个算法就不再说了,大家感兴趣的可以自己研究下。
找到一个效率高的矩阵乘法的算法,它是有着广泛的应用
综合解的工作量可能会增加,但增加的工作量不影响T(n)的阶还有另一种改进分治算法的策略是增加预处理,这个放在下一篇再说吧
尽信书,不如无书《孟子·尽心下》