20190822

T1过河：

题目描述

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0,1,…,L0,1,…,L（其中LL是桥的长度）。坐标为00的点表示桥的起点，坐标为LL的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是SS到TT之间的任意正整数（包括S,TS,T）。当青蛙跳到或跳过坐标为LL的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度LL，青蛙跳跃的距离范围S,TS,T，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

输入格式

第一行有11个正整数L(1 \le L \le 10^9)L(1≤L≤109)，表示独木桥的长度。

第二行有33个正整数S,T,MS,T,M，分别表示青蛙一次跳跃的最小距离，最大距离及桥上石子的个数，其中1 \le S \le T \le 101≤S≤T≤10,1 \le M \le 1001≤M≤100。

第三行有MM个不同的正整数分别表示这MM个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。

输出格式

一个整数，表示青蛙过河最少需要踩到的石子数。

输入输出样例

输入 #1复制

10
2 3 5
2 3 5 6 7

输出 #1复制

2

说明/提示

对于30%的数据，L \le 10000L≤10000；

对于全部的数据，L \le 10^9L≤109。

2005提高组第二题

#include
using namespace std;
int  st[10005],f[10005],L,s,t,n,a[10005],last=1,road,ans=1e9;
inline int read(){
	int k=0,f=1;
	char c=getchar();
	for(;!isdigit(c);c=getchar())
	  if(c=='-')
	    f=-1;
	for(;isdigit(c);c=getchar())
	  k=k*10+c-'0';
	return k*f;
}
int main(){
	L=read();
	s=read(),t=read(),n=read();
	for(int i=1;i<=n;i++)
	  a[i]=read();
	a[n+1]=L;
	sort(a+1,a+2+n);
	for(int i=1;i<=n;i++){
		road+=(a[i]-a[i-1])%t;
		if(a[i]-a[i-1]>=t)
		  road+=t;
		st[road]=1;
	}
	for(int i=1;i<=road+t;i++)
	  f[i]=1e9;
	f[0]=0;
	for(int i=1;i<=road+t;i++){
		for(int j=s;j<=t;j++)
		  if(i-j>=0) 
		  	f[i]=min(f[i],f[i-j]+st[i]);
	}
	for(int i=road;i<=road+t;i++)
	  ans=min(ans,f[i]);
	cout<

T2最优贸易：

题目描述

CC国有nn个大城市和mm 条道路，每条道路连接这 nn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mm 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 11条。

CC国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 CC 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 CC 国 n 个城市的标号从 1~ n1 n，阿龙决定从 11号城市出发，并最终在 nn 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 nn 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 CC 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

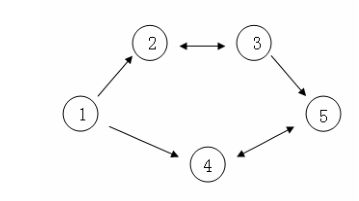
假设 CC国有 55个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

假设 1~n1 n 号城市的水晶球价格分别为 4,3,5,6,14,3,5,6,1。

阿龙可以选择如下一条线路：11->22->33->55，并在 22号城市以33 的价格买入水晶球，在 33号城市以55的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路11->44->55->44->55，并在第11次到达55 号城市时以 11的价格买入水晶球，在第 22 次到达44 号城市时以66 的价格卖出水晶球，赚取的旅费数为55。

现在给出 nn个城市的水晶球价格，mm 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入格式

第一行包含 22 个正整数nn和 mm，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 mm 行，每行有33个正整数x,y,zx,y,z，每两个整数之间用一个空格隔开。如果 z=1z=1，表示这条道路是城市xx到城市yy之间的单向道路；如果z=2z=2，表示这条道路为城市 xx和城市yy之间的双向道路。

输出格式

一 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 00。

输入输出样例

输入 #1复制

5 5 
4 3 5 6 1 
1 2 1 
1 4 1 
2 3 2 
3 5 1 
4 5 2 

输出 #1复制

5

说明/提示

【数据范围】

输入数据保证 11 号城市可以到达nn号城市。

对于 10%的数据，1≤n≤61≤n≤6。

对于 30%的数据，1≤n≤1001≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤1000001≤n≤100000，1≤m≤5000001≤m≤500000，1≤x1≤x，y≤ny≤n，1≤z≤21≤z≤2，1≤1≤各城市

水晶球价格≤100≤100。

NOIP 2009 提高组 第三题

#include
using namespace std;
struct edge{
	int u,v;
}e[1000005];
int f[1000005],dp[1000005],ne[2000005],n,m,c[1000005],bs,cho,cost[1000005],mx,x,y;
inline int read()
{
    int k=0,f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
      if(c=='-')
        f=-1;
    for(;isdigit(c);c=getchar())
      k=k*10+c-'0';
    return k*f;
}
inline void dfs(int x,int mn,int last){
	bool pd=false;
	mn=min(mn,c[x]);
	if(mndp[x])
	  dp[x]=mx,pd=true;
	if(!pd)
	  return;
	for(int i=f[x];i;i=ne[i])
	  dfs(e[i].v,mn,x);
	return;
}
int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++)
	  c[i]=read(),cost[i]=1e9;
	for(int i=1;i<=m;i++){
		x=read(),y=read(),cho=read();
		if(cho==1){
			e[++bs].u=x,e[bs].v=y;
			ne[bs]=f[e[bs].u],f[e[bs].u]=bs;
		}
		else{
			e[++bs].u=e[bs+1].v=x,e[bs].v=e[bs+1].u=y;
			ne[bs]=f[e[bs].u],f[e[bs].u]=bs;
			bs++;
			ne[bs]=f[e[bs].u],f[e[bs].u]=bs;
		}
	}
	dfs(1,1e9,0);
	cout<

T3双栈排序：

题目描述

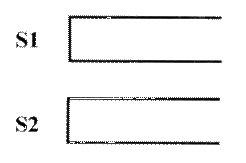
Tom最近在研究一个有趣的排序问题。如图所示，通过22个栈S_1S1​和S_2S2​，Tom希望借助以下44种操作实现将输入序列升序排序。

操作aa

如果输入序列不为空，将第一个元素压入栈S_1S1​

操作bb

如果栈S_1S1​不为空，将S_1S1​栈顶元素弹出至输出序列

操作cc

如果输入序列不为空，将第一个元素压入栈S_2S2​

操作dd

如果栈S_2S2​不为空，将S_2S2​栈顶元素弹出至输出序列

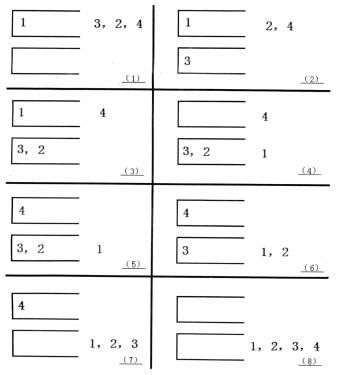
如果一个1-n1−n的排列P可以通过一系列操作使得输出序列为1,2,…,(n-1),n1,2,…,(n−1),n，Tom就称PP是一个“可双栈排序排列”。例如(1,3,2,4)(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)(2,3,4,1)不是。下图描述了一个将(1,3,2,4)(1,3,2,4)排序的操作序列：

当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)(1,3,2,4)，是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入格式

第一行是一个整数nn。

第二行有nn个用空格隔开的正整数，构成一个1-n1−n的排列。

输出格式

共一行，如果输入的排列不是“可双栈排序排列”，输出数字00；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入 #1复制

4
1 3 2 4

输出 #1复制

a b a a b b a b

输入 #2复制

4
2 3 4 1

输出 #2复制

0

输入 #3复制

3
2 3 1

输出 #3复制

a c a b b d

说明/提示

30\%30%的数据满足： n \le 10n≤10

50\%50%的数据满足：n \le 50n≤50

100\%100%的数据满足： n \le 1000n≤1000

#include
using namespace std;
bool pd;
int s[10005],q[10005],st,qt,a[10005],n,need=1,num=1,y,z;
char ans[10005];
inline int read(){
	int k=0,f=1;
	char c=getchar();
	for(;!isdigit(c);c=getchar())
	  if(c=='-')
	    f=-1;
	for(;isdigit(c);c=getchar())
	  k=k*10+c-'0';
	return k*f;
}
inline bool dfs(int x){
	if(!qt)
	  return true;
	for(y=x+1;y<=n;y++)
	  if(a[y]>a[x]&&a[y]>q[qt]) 
	    break;
    for(z=y+1;z<=n;z++) 
	  if(a[z]