拉格朗日插值--11次切比雪夫多项式零点作为节点Python实现并计算误差

目标函数

y=11+x2 y = 1 1 + x 2

条件

通过拉格朗日进行插值但是通过所给的节点的不同，会导致插值的效果也不同。

下面方法采用的是用等距节点来实现插值效果。

插值节点：
使用的是11次切比雪夫多项式的零点（扩展到指定的x空间）
也就是11个特定的节点。可以区别于之前的使用等距节点的情况

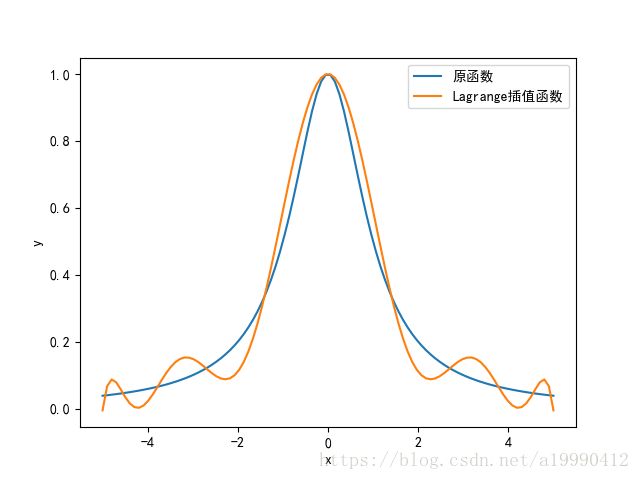
插值效果图

龙格现象基本不严重。虽然误差还存在，但基本算是吻合。
甚至比之前的最基础的埃尔米特插值更好。

代码

通过计算loss绝对值的均值，我们可以发现，用这种插值的方法只有接近0.05

import numpy as np
from sympy import *
import matplotlib.pyplot as plt


def f(x):
    return 1 / (1 + x ** 2)


def ChebyshevXGet():
    ans = np.array(list(map(lambda x: np.cos((21 - 2 * x) / 22 * np.pi), range(11))))
    return ans * 5


def draw(L):
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    x = np.linspace(-5, 5, 100)
    y = f(x)
    Ly = []
    for xx in x:
        Ly.append(L.subs(n, xx))
    plt.plot(x, y, label='原函数')
    plt.plot(x, Ly, label='Lagrange插值函数')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()

    plt.savefig('1.png')
    plt.show()


def lossCal(L):
    x = np.linspace(-5, 5, 101)
    y = f(x)
    Ly = []
    for xx in x:
        Ly.append(L.subs(n, xx))
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print(temp.mean())


if __name__ == '__main__':
    x = ChebyshevXGet()
    y = f(x)

    n, m = symbols('n m')
    init_printing(use_unicode=True)
    L = 0
    for k in range(11):
        temp = y[k]
        for i in range(11):
            if i != k:
                temp *= (n - x[i]) / (x[k] - x[i])
        L += temp
    lossCal(L)
    draw(L)