BubbleSort冒泡排序的理解

【纸上得来终觉浅，绝知此事要躬行】

废话不多说，网上有关冒泡排序的文章太多了，但是光看或者上来就使用别人最终优化的代码总会没有什么感觉。所以这次一点点通过代码，自己去感受一下优化的效果，文章是写给自己以后看的，我是个话痨，写的不会太专业。但是我还是要写！要感悟

开整！

先乱写一个数组，随便敲了16个元素，太少了没啥感觉。然后按照冒泡排序的思路去写了个算法，并添加一些记录参数供我们打印出来观察比较用。

private static int[] array = { 5, 2, 6, 17, 8, 39, 10, 11, 22, 13, 15, 9, 56, 1, 22, 27 };

public static void main(String[] args) {
    BubbleSort(array);
}

/**
  * 原始冒泡算法
  */ 
public static void BubbleSort(int[] array) {

    int round=0; //比较轮数
    int count=0; //比较次数
    int lastIndex=array.length-1; //末元素下标
    
    for (int i = 0; i < lastIndex; i++) {
        round++;
        System.out.println("********************   第" + round + "轮      ********************");
        System.out.println("比较元素：" +printSortUnit(array, lastIndex));
        for (int j = 0; j < lastIndex; j++) {
            if(array[j]>array[j+1]){
                swap(array, j, j+1);
            }
            count++;
            System.out.println("第"+count+"次       "+Arrays.toString(array));
        }
    }
}

/**
  * 交换数组元素
  */ 
public static void swap(int[] array, int p, int q) {
    int temp = 0;
    temp = array[p];
    array[p] = array[q];
    array[q] = temp;
}

/**
  * 打印需要比较的所有元素
  */
public static String printSortUnit(int[] array, int end) {
    StringBuffer str = new StringBuffer();
        str.append(array[0]);
        for (int i = 1; i <= end; i++) {
            str.append(","+array[i] );
        }
    return str.toString();
}

复制上面代码，跑一下，发现跑了15轮，每轮都比较了15次，所以一共15*15=225次比较。

这里说明一下，1次表示某两个相邻元素比较大小，1轮表示这16个元素从左往右比较完一遍。

我们可以发现，每一轮结束后数组从右往左就会依次从大到小排列好元素，所以我们把整个数组分为两块，左边一块是未排序完的元素数组，右边一块是从最大值开始依次排序的元素数组，并且未排序完的任意元素肯定小于已排序完的任意元素，所以我们可以将右边已排好序的“大元素”数组在下一轮的排序中剔除掉，只比较左边的这些元素并继续从大到小依次剔除即可。

 

第一次优化

很简单，改动一下j遍历即可：

/**
  *  冒泡算法第一次优化
  */
public static void BubbleSort1(int[] array) {
    int count=0;
    int round=0;
    int lastIndex = array.length-1;
    for (int i = 0; i < lastIndex; i++) {
        round++;
        System.out.println("********************   第" + round + "轮      ********************");
        System.out.println("比较元素：" +printSortUnit(array, lastIndex-i));
        for (int j = 0; j < lastIndex-i; j++) {
            if(array[j]>array[j+1]){
                swap(array, j, j+1);
            }
            count++;
            System.out.println("第"+count+"次       "+Arrays.toString(array));
        }
    }
}

这次再Run：

还是15轮，但是次数只用了120次！每一轮的比较元素都在一个一个减少，大大减少了比较次数。

 

第二次优化

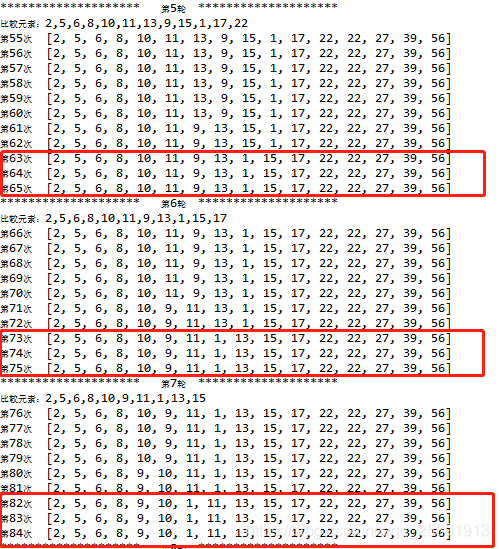
观察上面的图片可以发现在第13轮比较的元素为“2,1,5,6”还没有拍好，但是第14轮比较的元素为“1,2,5”，正好是排好序的，所以不管后面还要比较几轮都可以提前结束了。所以我们需要设置一个flag，如果某一轮比较元素时没有任何发生交换，说明这个数组已经排好序了，立刻结束。

代码如下：

/**
  *  冒泡算法第二次优化
  */
public static void BubbleSort2(int[] array) {
    int count=0;
    int round=0;
    int lastIndex = array.length-1;
    for (int i = 0; i < lastIndex; i++) {
        boolean isOver = true;
        round++;
        System.out.println("********************   第" + round + "轮      ********************");
        System.out.println("比较元素：" +printSortUnit(array, lastIndex-i));
        for (int j = 0; j < lastIndex-i; j++) {
            if(array[j]>array[j+1]){
                swap(array, j, j+1);
                isOver=false;
            }
            count++;
            System.out.println("第"+count+"次       "+Arrays.toString(array));
        }
        if(isOver){
            break;
        }
    }
}

运行结果正好在第14轮后就结束了，应该是数组元素不多的原因吧，所以比第一次优化只少了一轮比较，效果不明显，但确实是少了，不服气的小老弟可以多敲几十个元素再试试。

还能优化吗？可以！

 

第三次优化

我们还是从第二次优化的打印结果里找找看：

不难发现，每一轮我们都只是在一个个的去寻找【比较元素】里的最大值放在右边，但是如果【比较元素】里右边若干个元素已经排好序了，是不是就可以直接剔除比较了？

打个比方，如上图。第5轮，【比较元素】中17,22很明显已经是排好序的最大值，所以只需要比较前面十个元素即可，即比较9次即可。第6、7轮也是一样的问题。通俗点说只要后面N个元素比较后一直不发生交换，就说明这N个元素都是排好序了，且左边的元素都比这些值小（如果有大的肯定会通过交换推到右面），所以我们批量剔除这N个元素而不是每一轮只剔除一个最大元素。

因此，我们需要记录每一轮最后交换元素的位置changeIndex，下一轮直接遍历array[0]到array[changeIndex]即可，直到整轮一次交换都不发生（第二次优化的目的），就表示排序完成。

代码如下：

/**
 * 冒泡算法第三次优化
 */
public static void BubbleSort3(int[] array) {
    int count = 0;
    int round = 0;
    int lastIndex = array.length - 1;
    int changeIndex = lastIndex;
    for (int i = 0; i < lastIndex; i++) {
        int tempChangeIndex = -1;// 记录每一轮最后交换元素的下标
        round++;
        System.out.println("********************   第" + round + "轮      ********************");
        System.out.println("比较元素：" + printSortUnit(array, changeIndex));
        for (int j = 0; j < changeIndex; j++) {
            if (array[j] > array[j + 1]) {
                swap(array, j, j + 1);
                tempChangeIndex = j;
            }
            count++;
            System.out.println("第" + count + "次       " + Arrays.toString(array));
        }
        if (tempChangeIndex <= 0) {
            break; // 这里表示前两个元素交换或者一次都未交换的情况，均表示排序结束
        } else {
            changeIndex = tempChangeIndex;
        }
    }
}

几处改动：

1.添加一个变量changeIndex，用来控制每轮j从0循环到changeIndex，并在每轮结束后及时更新，给下一轮使用。

2.添加tempChangeIndex变量，在一轮中的每一次交换后更新，一轮全部结束后把这一轮最后一次交换元素的下标值赋给changeIndex变量。

（注：这里一定要分清changIndex是上一轮确定的值，tempChangeIndex是这一轮通过比较获得的值，tempChangeIndex一直小于changeIndex，两者不能混淆）

3.打印“比较元素”的下标也要改成changeIndex，而不是lastIndex-i。

4.因为tempChangeIndex自身表示交换元素的下标，当一轮比较结束后tempChangeIndex仍为“-1”时表示一次未交换，替代了之前的isOver==true（tempChangeIndex>=0表示isOver==false），所以可把isOver删掉了，tempChangeIndex为“0”时表示只有前两个元素交换，所以这里tempChangIndex为-1或者0都表示整个数组排序结束。代码最后的if语句就表示这个意思。

结果：

 

感悟：这一次比第二次优化又少了一轮，一共只比较了97次。反观最原始的225次确实少了很多，而且这个测试数组只有16个元素，如果是几万几十万甚至更多的数组元素需要排序的话，效果可想而知。

 

 

————————————————————————————————————————————————————————

算法思想总结：

我们根据冒泡算法的原理写了一个最原始的算法，然后根据结果优化了三次。

原始思想：每次都对N个元素两两相邻进行比较，比较N-1轮，每轮N-1次，排序完成。

第一次优化思想：从次的角度考虑，每一轮都能得到一个元素按顺序排在数组右边，这些排好序的元素不用参与后面的比较，故每一轮结束后剔除右边一个元素，下一轮只比较剩下的元素即可。

第二次优化思想：从轮的角度考虑，排序不一定要执行完N-1轮，当某一轮结束后未发生任何元素交换就表示已经排好顺序，不用继续比较了。

第三次优化思想：还是从次的角度考虑，是对第一次优化的再优化，第一次优化是一个一个剔除已排好序的元素，而第三次我们通过每轮最后一次交换元素的下标，快速排除已排好序的元素。一轮可剔除一个或多个最大有序元素。