【LOJ2722】「NOI2018」情报中心

【题目链接】

• 点击打开链接

【思路要点】

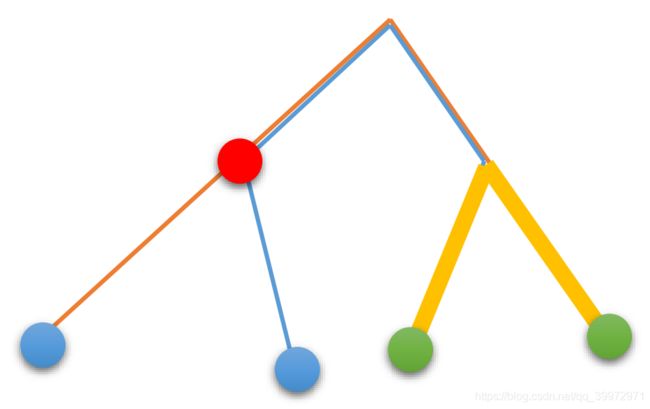
• 考虑特殊性质 $S2$ ，如下图，可以发现两条蓝-绿路径形成的链并的大小的两倍为 两条链长之和 $+$ 蓝点之间的距离 $+$ 绿点之间的距离 。
  
• 枚举蓝点的 $Lca$ ，即图中的红点，那么我们需要选出两个不属于同一个红点的子树的蓝点 $a,b$ ，使得它们对应的绿点 $p_a,p_b$ 满足最大的总收益减去总代价的差的两倍，也即最大化
  $$dist(p_a,p_b)+dist(a,p_a)-2cos{t}_{a,p_a}+dist(b,p_b)-2cos{t}_{b,p_b}+(dept{h}_a+dept{h}_b)-2dept{h}_{Lca}$$
• 由于我们已经枚举了 $Lca$ ，因此 $-2dept{h}_{Lca}$ 一项可以最后加上。
• 可以发现除 $dist(p_a,p_b)$ 一项以外 $a,b$ 相互独立，可以在 $p_a,p_b$ 各处挂上一个新叶子，维护最远点对。
• 在 $dfs$ 计算答案的过程中，我们需要支持集合合并，在合并的时候，求出跨越两个集合的最远点对。
• 对于非负边权的树，两个点集的并的最远点对的一端，一定是原来两个点集中，某个点集的最远点对的一端。这里我们新加的边可能权为负，但我们加入的节点均为叶子节点，可以将上述性质的证明稍作修改，使得其在这样的树上同样成立。
• 枚举每一个 $Lca$ ，在其路径两侧的点的虚树上分别运行特殊性质 $S2$ 的算法，我们可以计算所有路径的交包含两条路径的 $Lca$ 的情况。
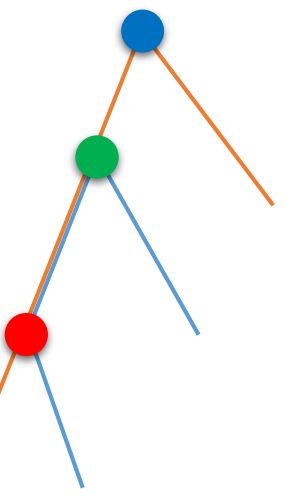
• 对于剩余情况，路径的交一定是一条不拐弯的祖孙链，如下图
  
• 枚举较深的交点，即图中红点，需要在满足两条链的下端点不在红点的同一子树中的情况下最大化 链的长度和 $-$ 链的权值和 $–$ 红点深度 $+$ max(绿点深度, 蓝点深度)
• 考虑采用线段树合并来维护蓝点集和绿点集，记录深度为 $i$ 的点对应的链长 $-$ 权值的最大值 $Maxv$ ，以及对应的链长 $-$ 权值 $+$ 深度的最大值 $Maxs$ 。
• 考虑线段树合并的过程，合并集合时，相当于枚举了所有可能的中间点 $mid$ ，保证蓝点在 $mid$ 的一侧，绿点在 $mid$ 的另一侧，可以直接用线段树上的信息更新答案。
• 时间复杂度 $O(NLogN+MLogN)$ 。

【代码】

#include
using namespace std;
const int MAXN = 1e5 + 5;
const int MAXP = 1e7 + 5;
const long long LOW = 1e16;
const long long INF = 4e18;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); } 
template <typename T> void read(T &x) {
	x = 0; int f = 1;
	char c = getchar();
	for (; !isdigit(c); c = getchar()) if (c == '-') f = -f;
	for (; isdigit(c); c = getchar()) x = x * 10 + c - '0';
	x *= f;
}
template <typename T> void write(T x) {
	if (x < 0) x = -x, putchar('-');
	if (x > 9) write(x / 10);
	putchar(x % 10 + '0');
}
template <typename T> void writeln(T x) {
	write(x);
	puts("");
}
struct Query {
	int x, y;
	ll cost;
};
vector <pair <int, ll>> a[MAXN];
vector <Query> q[MAXN]; ll ans, sum[MAXN];
int n, m, timer, dfn[MAXN], father[MAXN], depth[MAXN];
int tot, seq[MAXN], home[MAXN];
namespace rmq {
	const int MAXN = 1e5 + 5;
	const int MAXLOG = 18;
	int Min[MAXN][MAXLOG], Log[MAXN];
	int comb(int x, int y) {
		return (depth[x] < depth[y]) ? x : y;
	}
	int queryMin(int l, int r) {
		int len = r - l + 1, tmp = Log[len];
		return comb(Min[l][tmp], Min[r - (1 << tmp) + 1][tmp]);
	}
	void init(int *a, int n) {
		for (int i = 1; i <= n; i++) {
			Min[i][0] = a[i];
			Log[i] = Log[i - 1];
			if ((1 << (Log[i] + 1)) <= i) Log[i]++;
		}
		for (int t = 1; t < MAXLOG; t++)
		for (int i = 1, j = (1 << (t - 1)) + 1; j <= n; i++, j++)
			Min[i][t] = comb(Min[i][t - 1], Min[j][t - 1]);
	}
}
void dfs(int pos, int fa) {
	seq[++tot] = pos, home[pos] = tot, dfn[pos] = ++timer;
	father[pos] = fa, depth[pos] = depth[fa] + 1;
	for (auto x : a[pos])
		if (x.first != fa) {
			sum[x.first] = sum[pos] + x.second;
			dfs(x.first, pos);
			seq[++tot] = pos;
		}
}
inline int lca(int x, int y) {
	if (home[x] > home[y]) swap(x, y);
	return rmq :: queryMin(home[x], home[y]);
}
inline ll dist(int x, int y) {
	return sum[x] + sum[y] - 2 * sum[lca(x, y)];
}
struct SegmentTreeMerging {
	struct Node {
		int lc, rc; bool leaf;
		ll ans, Maxv, Maxs;
	} a[MAXP];
	int size, n;
	void init(int x) {
		n = x, size = 0;
		a[0].Maxs = a[0].Maxv = a[0].ans = -INF;
	}
	void update(int root) {
		a[root].ans = max(a[a[root].lc].ans, a[a[root].rc].ans);
		chkmax(a[root].ans, a[a[root].lc].Maxv + a[a[root].rc].Maxs);
		if (a[root].ans < -LOW) a[root].ans = -INF;
		a[root].Maxv = max(a[a[root].lc].Maxv, a[a[root].rc].Maxv);
		a[root].Maxs = max(a[a[root].lc].Maxs, a[a[root].rc].Maxs);
	}
	void modify(int &root, int l, int r, int pos, ll v, ll s, ll inc) {
		if (root == 0) {
			root = ++size;
			a[root].Maxs = -INF;
			a[root].Maxv = -INF;
			a[root].ans = -INF;
			a[root].leaf = false;
			a[root].lc = a[root].rc = 0;
		}
		if (l == r) {
			chkmax(a[root].Maxs, s);
			chkmax(a[root].Maxv, v);
			a[root].leaf = true;
			return;
		}
		int mid = (l + r) / 2;
		if (mid >= pos) {
			chkmax(ans, v + a[a[root].rc].Maxs + inc);
			modify(a[root].lc, l, mid, pos, v, s, inc);
		} else {
			chkmax(ans, s + a[a[root].lc].Maxv + inc);
			modify(a[root].rc, mid + 1, r, pos, v, s, inc);
		}
		update(root);
	}
	void modify(int &root, int pos, ll v, ll s, ll inc) {
		modify(root, 1, n, pos, v, s, inc);
	}
	void del(int root, int l, int r, int pos) {
		if (root == 0) return;
		if (l == r) {
			a[root].Maxs = -INF;
			a[root].Maxv = -INF;
			return;
		}
		int mid = (l + r) / 2;
		if (mid >= pos) del(a[root].lc, l, mid, pos);
		else del(a[root].rc, mid + 1, r, pos);
		update(root);
	}
	void del(int &root, int pos) {
		del(root, 1, n, pos);
	}
	int merge(int x, int y, ll inc) {
		if (x == 0 || y == 0) return x + y;
		if (a[x].leaf) {
			chkmax(a[x].Maxs, a[y].Maxs);
			chkmax(a[x].Maxv, a[y].Maxv);
			return x;
		}
		chkmax(ans, a[a[x].lc].Maxv + a[a[y].rc].Maxs + inc);
		chkmax(ans, a[a[y].lc].Maxv + a[a[x].rc].Maxs + inc);
		a[x].lc = merge(a[x].lc, a[y].lc, inc);
		a[x].rc = merge(a[x].rc, a[y].rc, inc);
		update(x);
		return x;
	}
	void join(int &to, int from, ll inc) {
		to = merge(to, from, inc);
	}
} ST;
namespace subtask1 {
	int root[MAXN];
	vector <pair <int, ll>> b[MAXN];
	void work(int pos, int fa) {
		for (auto x : a[pos])
			if (x.first != fa) {
				work(x.first, pos);
				ST.join(root[pos], root[x.first], -sum[pos]);
			}
		for (auto x : b[pos])
			ST.modify(root[pos], depth[x.first], x.second, x.second + sum[x.first], -sum[pos]);
		if (depth[pos] != 0) ST.del(root[pos], depth[pos] - 1);
	}
	void solve() {
		int Maxd = 0;
		for (int i = 1; i <= n; i++) {
			b[i].clear(), root[i] = 0;
			chkmax(Maxd, depth[i]);
		}
		ST.init(Maxd);
		for (int i = 1; i <= n; i++)
		for (auto x : q[i]) {
			ll len = sum[x.x] - sum[i] + sum[x.y] - sum[i];
			if (x.x != i) b[x.x].emplace_back(i, len - x.cost);
			if (x.y != i) b[x.y].emplace_back(i, len - x.cost);
		}
		work(1, 0);
	}
}
namespace subtask2 {
	struct info {
		ll res;
		pair <int, ll> x, y;
	};
	info merge(info a, info b, bool mode, ll inc) {
		if (a.x.first == 0) return b;
		if (b.x.first == 0) return a;
		info res; ll tmp;
		res.res = max(a.res, b.res);
		if (a.res == res.res) res.x = a.x, res.y = a.y;
		else res.x = b.x, res.y = b.y;
		tmp = dist(a.x.first, b.x.first) + a.x.second + b.x.second + inc;
		if (mode) chkmax(ans, tmp);
		if (tmp - inc > res.res) {
			res.res = tmp - inc;
			res.x = a.x, res.y = b.x;
		}
		tmp = dist(a.x.first, b.y.first) + a.x.second + b.y.second + inc;
		if (mode) chkmax(ans, tmp);
		if (tmp - inc > res.res) {
			res.res = tmp - inc;
			res.x = a.x, res.y = b.y;
		}
		tmp = dist(a.y.first, b.x.first) + a.y.second + b.x.second + inc;
		if (mode) chkmax(ans, tmp);
		if (tmp - inc > res.res) {
			res.res = tmp - inc;
			res.x = a.y, res.y = b.x;
		}
		tmp = dist(a.y.first, b.y.first) + a.y.second + b.y.second + inc;
		if (mode) chkmax(ans, tmp);
		if (tmp - inc > res.res) {
			res.res = tmp - inc;
			res.x = a.y, res.y = b.y;
		}
		return res;
	}
	info i[MAXN];
	vector <int> b[MAXN];
	void works2(int pos, bool root) {
		for (auto x : b[pos]) {
			works2(x, false);
			if (!root) i[pos] = merge(i[pos], i[x], true, -2 * sum[pos]);
		}
	}
	void solve(int root) {
		static bool vis[MAXN];
		vector <int> points;
		vis[root] = true;
		points.push_back(root);
		for (auto x : q[root]) {
			if (!vis[x.x]) {
				vis[x.x] = true;
				points.push_back(x.x);
			}
			if (!vis[x.y]) 	{
				vis[x.y] = true;
				points.push_back(x.y);
			}
		}
		sort(points.begin(), points.end(), [&] (int x, int y) {return dfn[x] < dfn[y]; });
		static int Stack[MAXN]; int top = 0;
		for (auto x : points) {
			if (top == 0) {
				Stack[++top] = x;
				b[x].clear();
			} else {
				int y = lca(x, Stack[top]);
				while (top >= 2 && depth[y] <= depth[Stack[top - 1]]) {
					b[Stack[top - 1]].push_back(Stack[top]);
					top--;
				}
				if (y == Stack[top]) {
					Stack[++top] = x;
					b[x].clear(), i[x] = (info) {-INF, make_pair(0, 0), make_pair(0, 0)};
				} else {
					b[y].clear(), i[y] = (info) {-INF, make_pair(0, 0), make_pair(0, 0)};
					b[y].push_back(Stack[top]);
					Stack[top] = y;
					Stack[++top] = x;
					b[x].clear(), i[x] = (info) {-INF, make_pair(0, 0), make_pair(0, 0)};
				}
			}
		}
		for (auto x : q[root]) {
			ll len = dist(x.x, x.y);
			if (x.x != root) i[x.x] = merge(i[x.x], (info) {-INF, make_pair(x.y, sum[x.x] + len - 2 * x.cost), make_pair(x.y, sum[x.x] + len - 2 * x.cost)}, true, -2 * sum[x.x]);
			if (x.y != root) i[x.y] = merge(i[x.y], (info) {-INF, make_pair(x.x, sum[x.y] + len - 2 * x.cost), make_pair(x.x, sum[x.y] + len - 2 * x.cost)}, true, -2 * sum[x.y]);
		}
		for (int i = 1; i <= top - 1; i++)
			b[Stack[i]].push_back(Stack[i + 1]);
		works2(root, true);
		vis[root] = false;
		for (auto x : q[root]) {
			vis[x.x] = false;
			vis[x.y] = false;
		}
	}
}
int main() {
	freopen("center.in", "r", stdin);
	freopen("center.out", "w", stdout);
	int T; read(T);
	while (T--) {
		read(n);
		for (int i = 1; i <= n; i++) {
			a[i].clear();
			q[i].clear();
		}
		for (int i = 1; i <= n - 1; i++) {
			int x, y, z; read(x), read(y), read(z);
			a[x].emplace_back(y, z);
			a[y].emplace_back(x, z);
		}
		timer = tot = 0, dfs(1, 0);
		rmq :: init(seq, tot);
		read(m);
		for (int i = 1; i <= m; i++) {
			int x, y, t; ll z; read(x), read(y), read(z);
			q[t = lca(x, y)].push_back((Query) {x, y, z});
		}
		ans = -INF;
		for (int i = 1; i <= n; i++)
			subtask2 :: solve(i);
		if (ans >= -LOW) ans /= 2;
		subtask1 :: solve();
		if (ans < -LOW) puts("F");
		else writeln(ans);
	}
	return 0;
}