Dijkstra算法中的A*改进

 

A*算法在Dijkstra算法中的应用

 

目录

 

1.参考资料

2.具体原理

2.1A*算法原理

2.1.1启发式搜索

2.1.2A*算法

2.2Dijkstra算法的改进

2.2.1松弛技术

2.2.2改进

3.改进结果

3.1改进目标

3.2运行结果

---

 

这是一个算法上机题对Dijkstra算法中松弛技术的改进，引入了启发式搜索，即A*算法的思想，学了一天了，现总结于此

 

 

1.参考资料

1.A*算法的一个具体实例讲解：

http://www.cppblog.com/christanxw/archive/2006/04/07/5126.html

 

2.启发式寻路算法总结（包含Dijkstra算法的讨论）

http://www.gaccob.com/publish/2015-05-28-path-finding.html#dijkstra?tdsourcetag=s_pcqq_aiomsg

 

3.A*算法中启发函数的使用

https://blog.csdn.net/free4wuyou/article/details/15676597

 

 

以上是关于A*和Dijkstra的具体讨论，其中

网址1比较具体也比较简单的介绍了A*算法的一个实例；

网址2则是提纲挈领，比较好的总结了多种启发式寻路算法，也给出了启发函数的明确定义；

网址3则是讲解了不同启发函数对算法性能的影响，并给出能得到最优解的条件——如果h(n)总是小于(或者等于)从结点n走到目标结点的步数,那么A*算法是一定可以找到最优路径的。

 

2.具体原理

2.1A*算法原理

2.1.1启发式搜索

盲目搜索会浪费很多时间和空间, 所以我们在路径搜索时, 会首先选择最有希望的节点, 这种搜索称之为 "启发式搜索 (Heuristic Search)"

如何来界定"最有希望"? 我们需要通过 启发函数 (Heuristic Function) 计算得到.

即在最短路径搜索时，当前点到目标点的一个估计函数（估计成本）。

常用的启发函数有：

1. 曼哈顿距离(Manhattan distance) 
2. 切比雪夫距离(Chebyshev distance) 
3. 欧氏距离(Euclidean distance)
4. Octile 距离

具体参照，网址2：

http://www.gaccob.com/publish/2015-05-28-path-finding.html#dijkstra?tdsourcetag=s_pcqq_aiomsg

 

下文中启发函数用h(n)表示，其意义为

h(n) 代表从当前点 n 到目标点 S 的估算开销, 即启发函数.

 

原来的从起点到当前点路径长度用g(n)表示，其意义为

g(n): 从起始点到当前点 n 的开销, 在网格地图中一般就是步长

2.1.2A*算法

 

A-Star 俗称 A , 是应用最广的寻路算法, 在很多场景下都适用. A 兼顾了 Dijkstra 的准确度和 BFS 的效率.

• f(n) = g(n) + h(n) , g(n) 和 h(n) 的定义同上
• 当 g(n) 退化为 0, 只计算 h(n) 时, A* 即退化为 BFS.
• 当 h(n) 退化为 0, 只计算 g(n) 时, A* 即退化为 Dijkstra 算法.
• 将起始点 S 加入 open-list.
• 从当前的 open-list 中选取 f(n) 最优(最小)的节点 n, 加入 close-list
• 遍历 n 的后继节点 ns
• 如果 ns 是新节点, 加入 open-list
• 如果 ns 已经在 open-list 中, 并且当前 f(ns) 更优, 则更新 ns 并修改 parent
• 迭代, 直到找打目标节点 D.

A 算法在从起始点到目标点的过程中, *尝试平衡 g(n) 和 h(n), 目的是找到最小(最优)的 f(n).

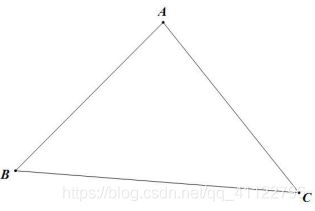
这里解释一下A*对Dijkstra改进的好处，在一张大地图中，此时的模型为欧氏平面，路径长即为欧氏距离，并且存在着三角形不等式

AB+AC>BC

由此知，在地图的最短路径的搜索中，并不是盲目搜索(Dijkstra是优先从当前最短路径的点搜索)效率最高，而是大致朝着终点方向搜索最快收敛，因为两点之间直线段最短，此时可以在Dijkstra算法中改变其松弛技术来做到这一点。

2.2Dijkstra算法的改进

2.2.1松弛技术

这里的松弛是指边的松弛和点的松弛，具体定义见算法书P418.这里简单说明

边的松弛。 松弛边v-> w意味着测试从s到w的最佳已知方式是从s到v，然后从v到w的边缘，如果是，则更新我们的数据结构。

顶点松弛。 我们所有的实现实际上都松弛了从给定顶点指向的所有边。

 

Dijkstra算法即是加点法，即从起点出发，遍历测试松弛起点邻接的每一个点，然后将最小的边加入最小生成树。

这里设起点s，边e(v,w)，终点t，路径长度函数为d[v]，即表示s到v的最短路径长。这里d其实就是上文的g。

则松弛边e为

If(d[w]>d[v]+e)

{

d[w]=d[v]+e;

将该边加入树；

}

 

但Dijkstra算法每次都是检查树中最短路径的点，这不一定是我们要的查找方向——大致朝着终点方向搜索。

2.2.2改进

此时采用启发式搜索，引入新的度量D[v]（即f）代替d[v]（即g），加入当前点到终点的欧氏距离

D[v]=d[v]+distance(v,t)

(f(n)=g(n)+h(n))

这里启发函数h(n)即为

h(v)=distance(v,t)

即顶点v到终点t的欧氏距离。

 

则松弛边e为

If(D[w]>D[v]-distance(v,t)+e(v,w)+distance(w,t))

{

D[w]=D[v]-distance(v,t)+e(v,w)+distance(w,t);

将该边加入树；

}

这里解释下为什么D[w]更新为如上式子，由D[w]定义

D[w]=d[w]+distance(w,t)      式1

又d[w]是s->w路径长，此时边e(v,w)的另一个端点为v,松弛该边，则应测试s->v+v->w的路径长，故把d[w]写为

d[w]=d[v]+e(v,w) 式2

此时式1变为

D[w]=d[v]+e(v,w)+distance(w,t) 式3

此时求d[v],由于此时只储存了新度量D，故从D[v]表达式入手

D[v]=d[v]+distance(v,t)

得d[v]

d[v]=D[v]-distance(v,t) 式4

将式（4）代入式（3）即得改进条件

D[w]=D[v]-distance(v,t)+e(v,w)+distance(w,t); 式5

式（5）即是Dijkstra算法的A*改进，或称启发式搜索改进。

此时搜索方向大致朝着终点方向搜索，并且由于三角形不等式，易证明该算法能够得到最优路径：

如果h(n)总是小于(或等于)从结点n走到目标结点的步数（这里三角形不等式提供保证）,那么A*算法是一定可以找到最优路径的。

 

3.改进结果

3.1改进目标

目标2即为A*算法

3.2运行结果

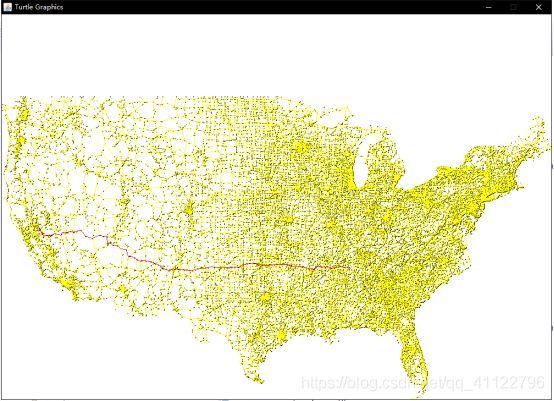
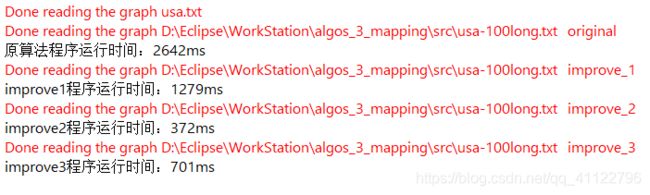
原算法，求0-5000的路径

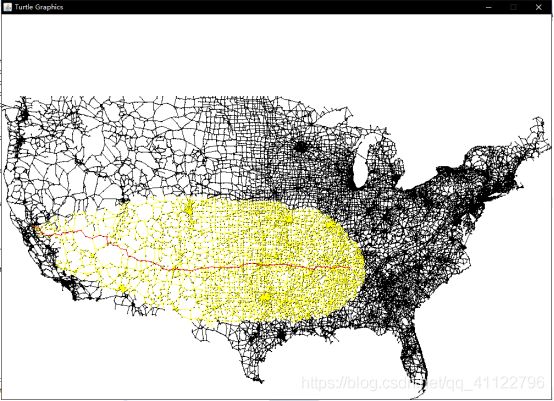
改进1，到d就停止搜索

 

改进2，启发式搜索

 

改进3，多路堆，我采用了8路堆

搜索100个查询性能比较