算法(2)——排序1.0

总结下最简单的最常用的排序算法冒泡排序、插入排序、选择排序

对于排序算法执行效率的分析，我们一般会从这几个方面来衡量：
1.最好情况、最坏情况、平均情况时间复杂度
我们在分析排序算法的时间复杂度时，要分别给出最好情况、最坏情况、平均情况下的时间复杂度。
2.时间复杂度的系数、常数 、低阶
我们知道，时间复杂度反应的是数据规模n很大的时候的一个增长趋势，所以它表示的时候会忽略系数、常数、低阶。但是实际的软件开发中，我们排序的可能
是10个、100个、1000个这样规模很小的数据，所以，在对同一阶时间复杂度的排序算法性能对比的时候，我们就要把系数、常数、低阶也考虑进来。
3.比较次数和交换（或移动）次数
基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外。不过，针对排序算法的空间复杂度，我们还引入了一个新的概念，原地排序（Sorted in place）。原地排序算法，就是特指空间复杂度是O(1)的排序算法。

排序算法的稳定性

仅仅用执行效率和内存消耗来衡量排序算法的好坏是不够的。针对排序算法，我们还有一个重要的度量指标，稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

排序算法是否稳定有什么用处：

稳定的排序算法代表着在排序之后相等的元素前后位置不会调换
场景：订单按照价格排序，如果价格相同则按照，时间先后排序
一般的先按照价格排序，再按照时间来排，之前的顺序就会被打乱，所以先按照时间来排序，然后用一个原地排序的算法就可以满足这个场景。

1.冒泡排序

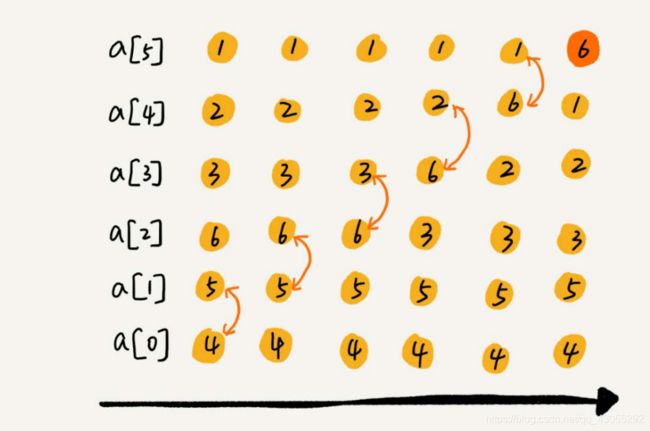
比较，交换。一次循环保证有一个数到了正确的位置。

全部循环完后，所有数有序。当然也有可能在一开始或者是到中途的时候，数组就已经是有序的了，可以加一个终止条件如果不进行比较，就可以结束循环。代码如下

/**
     *冒泡排序
     * @param array
     * @return
     */
    public static int[] bubbleSort(int[] array){
        int transit;
        boolean end;
        for (int i = 0 ; i< array.length; i++){
            end = true;
            for (int j = i ; j < array.length ; j++){
                if (array[i] < array[j]){
                    transit = array[i];
                    array[i] = array[j];
                    array[j] = transit;
                    end = false;
                }
            }
            if (end == true){
                break;
            }
        }
        return array;
    }

分析得出冒泡排序的最坏情况，数组完全完全逆序，时间复杂度是O(n2),最好情况数组原本就是有序的，时间复杂度是O(n），平均时间复杂度是O(n2)。
冒泡排序不用额外的存储空间，因此是原地排序。
冒泡排序可以让两数相等的情况下前后不进行交换，所以是稳定的排序算法。

2.插入排序

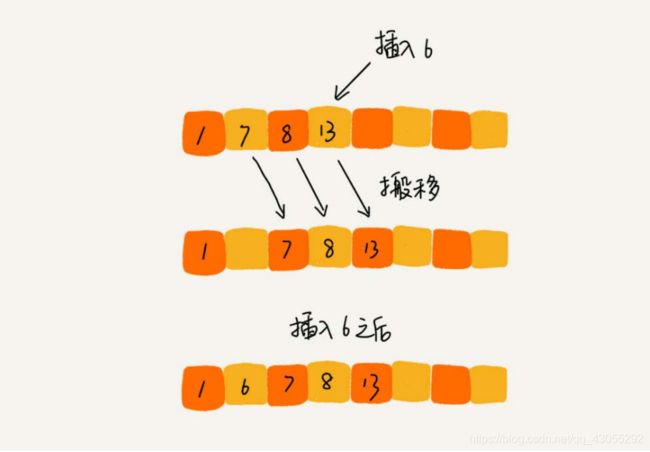
从第二个数开始循环，与前面的数相比较，比选中的数大，往后移动一位，知道找到不大于选中的那个数为止，插入，前面的是有序的区间后边的是无序的区间。

代码如下：

/**
     *插入排序
     * @param array
     * @return
     */
    public static int[]insertSort(int[] array){
        int value;
        for (int i = 1; i < array.length; i++) {
            value = array[i];
            int j;
            for (j = i-1; j >= 0; j--) {
                if (value>array[j]){
                    array[j+1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1]=value;
        }
        return array;
    }

最坏情况时间复杂度跟每一个数据都要比较，都要数据搬移时间复杂度是O(n2),最好情况是只要遍历比较一遍不需要数据的搬移时间复杂度是O(n),
平均时间复杂度每插入一次的时间复杂度是O(n),外边要循环N次，因此平均是O(n2)
插入排序不用额外的存储空间，因此是原地排序。
插入排序可以让两数相等的情况下前后不进行交换，所以是稳定的排序算法。

3.选择排序

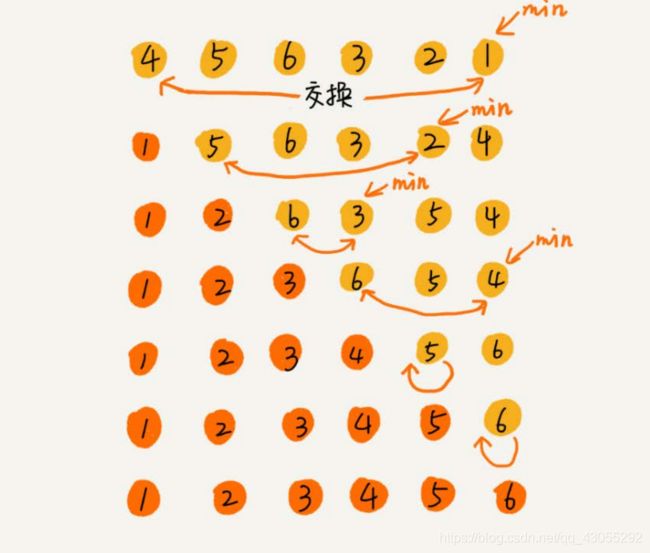
选取后边区间最小的数，与第一个数进行交换 ，第二小的与第二个数交换
代码如下：

/**
     *选择排序
     * @param array
     * @return
     */
    public static int[] selectSort(int[] array){
        int max;
        for (int i = 0; i < array.length; i++) {
            for (int j = i+1; j < array.length; j++) {
                if (array[i] < array[j]){
                    max = array[j];
                    array[j] = array[i];
                    array[i] = max;
                }
            }
        }
        return array;
    }

选择排序无论如何都会把两轮循环走完，最好，最坏，平均时间复杂度都是O(n2)
选择排序也没有用到新的空间，所以也是原地排序
然后每次挑选最小的，与i位置的数据交换，有可能相同的数前后顺序会有改变，比如9，9，2，5，1 第一个9就会到第二个9后边