数据结构二叉树个人总结
参考:
大话数据结构
http://blog.csdn.net/luckyxiaoqiang/article/details/7518888
http://blog.csdn.net/ns_code/article/details/12977901
http://10741357.blog.51cto.com/10731357/1767450
相关概念
树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:(1)有且仅有一个特定的称为根(root)的节点;(2)当n>1时,其余节点客分为m(m>0)个互不相交的有限集T1、T2、….、Tm,其中每一个集合体本身又是一棵树,并且称为根的子树(SubTree),如图
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根节点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成,如图,
二叉树性质:
1. 在二叉树的第i层上至多有2^(i-1)个结点(i>=1).
2. 深度为k的二叉树至多有2^k-1个结点(k>=1)
3. 对任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,,则n0=n2+1。
4. 具有n个结点的完全二叉树的深度为[log2(n)]+1([x]表示不大于x的最大整数)。
5. 如果对一颗有n个结点的完全二叉树的节点按层序编号,对任一结点i(1<=i<=n)有:
a) 如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是节点[i/2];
b) 如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是节点2*i;
c) 如果2*i+1>n,则结点i无右孩子;否则其右孩子是结点2*i+1。
二叉树节点定义如下:
typedef struct _BinaryTreeNode
{
int m_nValue;
struct _BinaryTreeNode *m_pLeft;
struct _BinaryTreeNode *m_pRight;
}BTNode;二叉树相关问题
1遍历二叉树(递归与非递归)
遍历二叉树的算法有前序遍历、中序遍历、后序遍历和层序遍历。
假设D代表根结点,L代表左子树,R代表右子树,则前三种遍历算法跟别对应这DLR,LDR,LRD。
代码主体:
#include <iostream>
using namespace std;
typedef struct _BinaryTreeNode
{
int m_nValue;
struct _BinaryTreeNode *m_pLeft;
struct _BinaryTreeNode *m_pRight;
}BTNode;
int main()
{
//======================创建二叉树==============
BTNode *T1 = new BTNode;
BTNode *T2 = new BTNode;
BTNode *T3 = new BTNode;
BTNode *T4 = new BTNode;
BTNode *T5 = new BTNode;
BTNode *T6 = new BTNode;
T1->m_nValue = 3;
T1->m_pLeft = T2;
T1->m_pRight = T3;
T2->m_nValue = 1;
T2->m_pLeft = T4;
T2->m_pRight = T5;
T3->m_nValue = 5;
T3->m_pLeft = T6;
T3->m_pRight = NULL;
T4->m_nValue = 4;
T4->m_pLeft = NULL;
T4->m_pRight = NULL;
T5->m_nValue = 2;
T5->m_pLeft = NULL;
T5->m_pRight = NULL;
T6->m_nValue = 6;
T6->m_pLeft = NULL;
T6->m_pRight = NULL;
//===============遍历算法
//PreOrderTraverse(T1);
delete T1, T2, T3, T4, T5, T6;
return 0;
}前序遍历递归解法:
(1)如果二叉树为空,空操作
(2)如果二叉树不为空,访问根节点,前序遍历左子树,前序遍历右子树
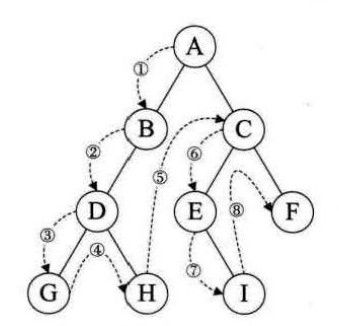
参考代码如下:
void PreOrderTraverse(BTNode *T)
{
if (T == NULL)
return;
cout << T->m_nValue << " "; //打印根结点的值
PreOrderTraverse(T->m_pLeft);//遍历左子树
PreOrderTraverse(T->m_pRight);//遍历右子树
}中序遍历递归解法:
(1)如果二叉树为空,空操作。
(2)如果二叉树不为空,中序遍历左子树,访问根节点,中序遍历右子树

参考代码如下:
void InOrderTraverse(BTNode *T)
{
if (T == NULL)
return;
InOrderTraverse(T->m_pLeft);//遍历左子树
cout << T->m_nValue << " "; //打印根结点的值
InOrderTraverse(T->m_pRight);//遍历右子树
}后序遍历递归解法:
(1)如果二叉树为空,空操作
(2)如果二叉树不为空,后序遍历左子树,后序遍历右子树,访问根节点
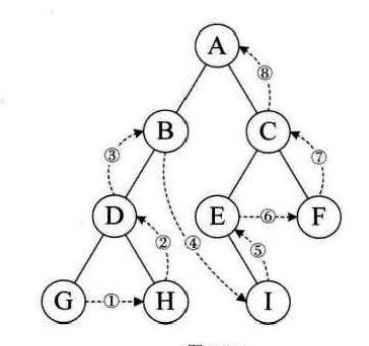
参考代码如下:
void PostOrderTraverse(BTNode *T)
{
if (T == NULL)
return;
PostOrderTraverse(T->m_pLeft);//遍历左子树
PostOrderTraverse(T->m_pRight);//遍历右子树
cout << T->m_nValue << " "; //打印根结点的值
}层序遍历解法:
层序遍历相当于广度优先搜索,把二叉树从上到下,从左到右进行遍历
使用队列实现。先初始化队列,将根节点压入队列。当队列不为空,进行如下操作:弹出一个节点,访问,若左子节点或右子节点不为空,将其压入队列。

参考代码:
#include 前序遍历非递归解法:
前序遍历先遍历根结点,再遍历左、右节点。因此当遍历到当前节点时,下一步要遍历左子树,如果左子树不为空,那么右子树的内容需要存起来,以便后用。根据递归的思想,先经过的节点右子树,应该后访问,所以我们选择栈来保存右子树的根结点。
当左子树为空的时候,我们要遍历当前节点的右子树,而右子树的根结点保存在栈中的,因此我们把出战的节点当做当前节点,再次判断左右节点是否为空。
直到最后左子树为空并且栈也为空的时候,便利完成。
参考代码:
void PreOrderTraverse_NonRecursive(BTNode *T)
{
stack中序遍历非递归解法:
中序遍历先遍历左子树,在遍历根结点、右子树,所以我们同样需要一个栈来保存遍历时的根结点。
中序遍历在遍历子树的时候,总是从子树的最左端下段开始,因此我们需要找到以当前节点为根结点的左子树的叶子节点,并且保存一路经过的根结点。
当左子树为空的时后,弹出栈里的根结点,访问根结点之后,再访问以右孩子为根结点的子树,此时我们仍然要找最左下方的叶子节点最先访问。
当前节点的右子树访问完毕后,再从栈中弹出当前节点的双亲节点,依次遍历左子树,根结点和右子树。
参考代码:
BTNode* FindLeftLeaf(BTNode *pT, stack后序遍历非递归解法:
后序遍历先遍历左子树,再遍历右子树,最后遍历根结点,所以在入栈的时候,当前根结点在最下边,其次是右孩子,再者是左孩子。然后把左孩子当做当前节点。
如果当前节点有左右孩子,则重复上面的步骤
如果当前结点没有孩子节点,或者当前结点的左孩子或右孩子已经被访问过,那么当前结点就要弹出,置下一个结点为当前结点。重复该步骤。
参考代码:
void PostOrderTraverse_NonRecursive(BTNode *pT)
{
if (pT == NULL)
return;
stack<BTNode *> s_BTNode;
BTNode *pCur = pT;
BTNode *pPre = pT;
s_BTNode.push(pCur); //当前结点入栈
while (!s_BTNode.empty()) //当栈不为空
{
pCur = s_BTNode.top(); //取栈的第一个节点为当前结点
if (pCur->m_pLeft == NULL&&pCur->m_pRight == NULL) //如果当前结点是叶子结点,弹出该结点
{
cout << pCur->m_nValue << " ";
pPre = pCur; //把当前结点设置为已弹出子节点
s_BTNode.pop();
}
else if (pCur->m_pLeft == pPre || pCur->m_pRight == pPre)//如果当前结点的子节点是已弹出的,说明这个节点也应该弹出了
{
cout << pCur->m_nValue << " ";
pPre = pCur; //把当前结点设置为已弹出子节点
s_BTNode.pop();
}
else
{
if (pCur->m_pRight != NULL) //如果右子节点不为空,压入栈内
s_BTNode.push(pCur->m_pRight);
if (pCur->m_pLeft != NULL) //如果左子节点不为空,压入栈内
s_BTNode.push(pCur->m_pLeft);
}
}
}2二叉树线索化和遍历
我们在二叉树中,只能知道每个结点指向其左右孩子结点的地址,而不知道某个结点的前驱是谁,后继是谁。然而,二叉树中有些结点的左右孩子指向的是空指针,我们可以利用这些空着的地址,存放该节点的前驱和后继,那么我们便可实现我们之前的目的了
我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就成为线索二叉树(Threaded Binary Tree)。
后继线索化:
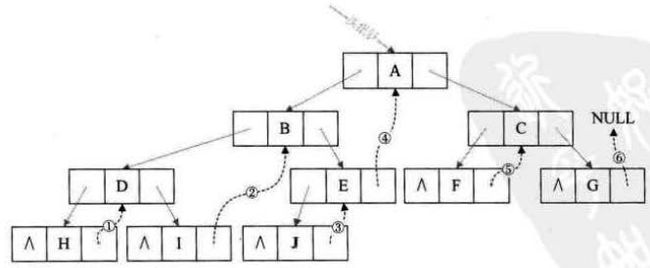
前驱线索化:

我们对二叉树以某种次序遍历使其变为线索二叉树的过程称为线索化。
二叉树的二叉线索存储结构定义:
typedef enum {Link,Tread} PointerTag;//Link==0表示指向左右孩子指针;Tread==1表示指向左右孩子指针
typedef struct BiThrNode
{
char data;
struct BiThrNode *pLChild,*pRChild;
PointerTag Ltag,Rtag;
}BiThrNode;线索化通用代码:
#include <iostream>
using namespace std;
typedef enum { Link, Thread } PointerTag;//Link==0表示指向左右孩子指针;Thread==1表示指向左右孩子指针
typedef struct BiThrNode
{
char data;
struct BiThrNode *pLChild, *pRChild;
PointerTag Ltag, Rtag;
}BiThrNode;
int main()
{
BiThrNode *N1, *N2, *N3, *N4, *N5, *N6;
N1->data = 'A';
N1->Ltag = Link;
N1->Rtag = Link;
N1->pLChild = N2;
N1->pRChild = N3;
N1->data = 'B';
N1->Ltag = Link;
N1->Rtag = Link;
N1->pLChild = N4;
N1->pRChild = N5;
N1->data = 'C';
N1->Ltag = Link;
N1->Rtag = Thread;
N1->pLChild = N6;
N1->pRChild = NULL;
N1->data = 'D';
N1->Ltag = Thread;
N1->Rtag = Thread;
N1->pLChild = NULL;
N1->pRChild = NULL;
N1->data = 'E';
N1->Ltag = Thread;
N1->Rtag = Thread;
N1->pLChild = NULL;
N1->pRChild = NULL;
N1->data = 'F';
N1->Ltag = Thread;
N1->Rtag = Thread;
N1->pLChild = NULL;
N1->pRChild = NULL;
BiThrNode *Pre = new BiThrNode;
//==============测试代码
//InOrderThreading(N1, Pre);
//InOrderTraverse_Thread(N1);
//==============测试代码
delete N1, N2, N3, N4, N5, N6, Pre;
return 0;
}前序线索化递归解法:
void PreOrderThreading(BiThrNode *pCur, BiThrNode* &pPre)//由于前驱结点的值一直是变得,所以这里用索引传值,保证每次迭代*pPre的准确性
{
if (pCur == NULL)
return;
if (pCur->pLChild == NULL) //当前结点没有左孩子
{
pCur->Ltag = Thread; //把当前节点左标志位置为Thread
pCur->pLChild = pPre; //当前节点左孩子指向前驱
}
if (pPre->pRChild == NULL) //前驱结点没有右孩子
{
pPre->Rtag = Thread; //前驱节点右标志位置为Thread
pPre->pRChild = pCur; //前驱结点右孩子指向后继(当前结点)
}
pPre = pCur; //当前结点赋给前驱结点
//经过了上面的步骤,由于pPre不可能是NULL了,所以在迭代的时候,判断条件要进行修改
if (pCur->Ltag==Link)
PreOrderThreading(pCur->pLChild, pPre);
if (pCur->Rtag==Link)
PreOrderThreading(pCur->pRChild, pPre);
}中序线索化递归解法:
void InOrderThreading(BiThrNode *pCur, BiThrNode* &pPre)
{
if (pCur == NULL)
return;
InOrderThreading(pCur->pLChild,pPre);
if (pCur->pLChild == NULL) //当前结点没有左孩子
{
pCur->Ltag = Thread; //把当前节点左标志位置为Thread
pCur->pLChild = pPre; //当前节点左孩子指向前驱
}
if (pPre->pRChild == NULL) //前驱结点没有右孩子
{
pPre->Rtag = Thread; //前驱节点右标志位置为Thread
pPre->pRChild = pCur; //前驱结点右孩子指向后继(当前结点)
}
pPre = pCur; //当前结点赋给前驱结点
InOrderThreading(pCur->pRChild,pPre);
}后序线索化递归解法:
void PostOrderThreading(BiThrNode *pCur, BiThrNode* &pPre)
{
if (pCur == NULL)
return;
InOrderThreading(pCur->pLChild, pPre);
InOrderThreading(pCur->pRChild, pPre);
if (pCur->pLChild == NULL) //当前结点没有左孩子
{
pCur->Ltag = Thread; //把当前节点左标志位置为Thread
pCur->pLChild = pPre; //当前节点左孩子指向前驱
}
if (pPre->pRChild == NULL) //前驱结点没有右孩子
{
pPre->Rtag = Thread; //前驱节点右标志位置为Thread
pPre->pRChild = pCur; //前驱结点右孩子指向后继(当前结点)
}
pPre = pCur; //当前结点赋给前驱结点
}三种线索化的方案其实同遍历二叉树的方法差不多,就是在访问节点的那一步进行了变动。线索化的时候,需要一个前驱指针和一个当前指针一起遍历这个二叉树,当前指针的左孩子为空时就指向前驱结点,而前驱结点的右孩子为空的时候就指向当前节点。
线索化二叉树的遍历:
中序遍历:
void InOrderTraverse_Thread(BiThrNode *pHead)
{
BiThrNode *pCur = pHead;
if (pCur == NULL)
return;
while (pCur != NULL)
{
//找到该子树中最左边的叶子节点,访问数据
while (pCur->Ltag == Link)
pCur = pCur->pLChild;
cout << pCur->data << " ";
//当前结点右标识位为Thread,把当前结点的后继(右孩子)置为当前节点,并访问数据,否则把右孩子置为当前节点,并找该子树的最左叶子节点。
while (pCur->Rtag == Thread&&pCur->pRChild!=NULL)
{
pCur = pCur->pRChild;
cout << pCur->data << " ";
}
pCur = pCur->pRChild;
}
}