二叉查找树，AVL树，伸展树【CH4601普通平衡树】

最近数据结构刚好看到了伸展树，在想这个东西有什么应用，于是顺便学习一下。

 

二叉查找树（BST），对于树上的任意一个节点，节点的左子树上的关键字都小于这个节点的关键字，节点的右子树上的关键字都大于这个节点的关键字。

对二叉查找树进行中序遍历，可以得到一个有序的序列。

下面这些操作的期望复杂度是$O(log N)$，但是如果BST中的数据是有序的序列BST就会变成一条链，复杂度会退化成$O(N)$

 

为了避免越界减少边界情况的特殊判断，一般在BST中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。

 1 struct BST {
 2     int l, r;
 3     int val;
 4 }a[SIZE];
 5 int tot, root, INF = 1 << 30;
 6 
 7 int NEW(int val)
 8 {
 9     a[++tot].val = val;
10     return tot;    
11 } 
12 
13 void build()
14 {
15     NEW(-INF), NEW(INF);
16     root = 1;
17     a[1].r = 2;
18  } 

检索时，如果当前节点p的关键字等于val，则已经找到。

如果p的关键字大于val，如果p的左子节点为空说明val不存在，否则在p的左子树中递归进行检索。

如果p的关键字小于val，如果p的右子节点为空说明val不存在，否则在p的右子树中递归进行检索。

1 int Get(int p, int val)
2 {
3     if(p == 0)return 0;
4     if(val == a[p].val)return p;
5     return val < a[p].val ? Get(a[p].l, val) : Get(a[p].r, val);
6 }

插入时，先执行检索操作，知道发现走向的p的子节点为空说明val不存在时，直接建立新节点。

 1 void Insert(int &p, int val)
 2 {
 3     if(p == 0){
 4         p = New(val);
 5         return;
 6     }
 7     if(val == a[p].val) return;
 8     if(val < a[p].val) Insert(a[p].l, val);
 9     else Insert(a[p].r, val);
10 }

val的后继指的是在BST中关键码大于val的前提下，关键码最小的节点。

求后继的过程：初始化ans为具有正无穷关键码的那个节点的编号，然后在BST中检索val。检索过程中，每经过一个点，看看能不能更新ans

当检索完成后，可能没有找到val，此时ans就是答案。

也有可能找到了关键字是val的节点p，但是p没有右子树，那么ans也就是答案。

也有可能是p有右子树，那么说明val的后继不是在刚刚已经经过的那些节点中，所以还要从p的右子节点出发，一直往左走。

 1 nt GetNext(int val)
 2 {
 3     int ans = 2;
 4     int p = root;
 5     while(p){
 6         if(val == a[p].val){
 7             if(a[p].r > 0){
 8                 p = a[p].r;
 9                 while(a[p].l > 0) p = a[p].l;
10                 ans = p;
11             }
12             break;
13         }
14         if(a[p].val > val && a[p].val < a[ans].val)ans = p;
15         p = val < a[p].val ? a[p].l : a[p].r;
16     }
17     return ans;
18 }

删除节点时，也需要先检索val得到节点p。

如果p的孩子只有一个，那么可以直接删除，让p的子节点代替p。

如果p的孩子有两个，就需要在BST中找到val的后继节点nxt。

因为nxt没有左子树，所以可以直接让nxt的右子树代替nxt，然后让nxt代替p。

 1 void remove(int val)
 2 {
 3     int &p = root;
 4     while(p){
 5         if(val == a[p].val) break;
 6         p = val < a[p].val ? a[p].l : a[p].r;
 7     }
 8     if(p == 0)return ;
 9     if(a[p].l == 0){
10         p = a[p].r;
11     }
12     else if(a[p].r == 0){
13         p = a[p].l;
14     }
15     else{
16         int nxt = a[p].r;
17         while(a[nxt].l > 0)nxt = a[nxt].l;
18         remove(a[nxt].val);
19         a[nxt].l = a[p].l, a[nxt].r = a[p].r;
20         p = nxt;
21     }
22 }

 

AVL树，是带有平衡条件的二叉查找树。

每个节点的左子树和右子树的高度最多差1。这样就可以使整棵树的深度维持在$O(log N)$

要维持平衡的条件，主要改变的是插入时的操作。

当我们插入了一个节之后，某一条路径上的节点有可能平衡条件被破坏，这时候我们就需要进行旋转操作使他们重新达到平衡条件。

插入时，沿着节点到根更新平衡信息，找到第一个平衡被破坏了的节点（最深的一个）a。

a的两棵子树的高度差2，如果是对a的左儿子的左子树或a的右儿子的右子树进行插入，那么只用进行一次单旋转。

比如这样：

 

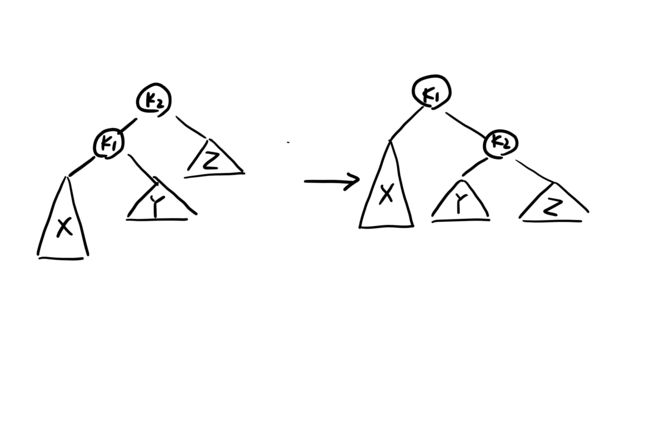
如果是对a的左儿子的右子树或是a的右儿子的左子树进行插入，需要进行一次双旋转。而实际上就是先将k1与k2进行一次旋转，再与k3旋转。

 

右旋就是把k1变成k2的父节点，k2作为k1的右子节点。zig(p)可以理解成把p的左子节点绕着p向右旋转。

1 void zig(int &p)
2 {
3     int q = a[p].l;
4     a[p].l = a[q].r, a[q].r = p;
5     p = q;
6 }

左旋zag(p)可以理解成把p的右子节点绕着p向左旋转。

1 void zag(int &p)
2 {
3     int q = a[p].r;
4     a[p].r = a[q].l, a[q].l = p;
5     p = q;
6 }

删除操作时，由于支持旋转，我们可以直接找到需要删除的节点，把他旋转成叶节点后直接删除。

 

伸展树（spaly tree），保证从空树开始任意连续M次对树的操作最多花费$O(M log N)$时间，但是并不排除任意一次操作花费$O(N)$时间的可能。

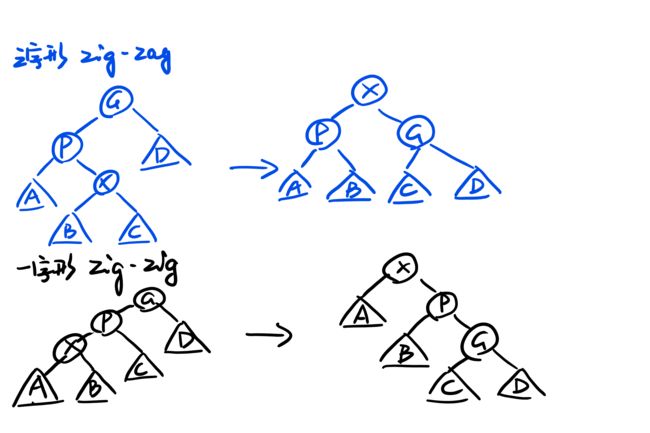
当一个节点被访问，就将他移动到根上。称为Splay操作。

Spaly操作：令X是在访问路径上的一个（非根）节点，如果X的父节点是树根，就只需要旋转X和树根。

否则分两种情况。

举个书上的习题作为例子。

在实际应用中，我们可以用伸展树维护一些区间的操作。

比如我们要提取区间[a,b]，那么我们将a前面一个数对应的结点转到树根，将b 后面一个结点对应的结点转到树根的右边，那么根右边的左子树就对应了区间[a,b]。

 

与线段树相比，伸展树功能更强大，它能解决以下两个线段树不能解决的问题：

（1） 在a后面插入一些数。方法是：首先利用要插入的数构造一棵伸展树，接着，将a 转到根，并将a 后面一个数对应的结点转到根结点的右边，最后将这棵新的子树挂到根右子结点的左子结点上。

（2）  删除区间[a,b]内的数。首先提取[a,b]区间，直接删除即可。

关于伸展树的实现代码可以参考kuangbin博客中的转载

 

CH上有一道模板例题

http://contest-hunter.org:83/contest/0x40「数据结构进阶」例题/4601%20普通平衡树

要求实现一下六种操作：

1. 插入x数
2. 删除x数(若有多个相同的数，因只删除一个)
3. 查询x数的排名(若有多个相同的数，因输出最小的排名)
4. 查询排名为x的数
5. 求x的前驱(前驱定义为小于x，且最大的数)
6. 求x的后继(后继定义为大于x，且最小的数)

因为给的数可能会重复，而删除时只能删除一个，所以用cnt来记录这个值出现了的次数。

还要求查询排名，所以给节点增加一个size属性，记录以该节点为根的子树中所有节点的cnt之和。

在插入、删除和旋转时从下往上更新size信息。

  1 //#include
  2 #include
  3 #include
  4 #include
  5 #include
  6 #include
  7 #include 
  8 #include

 

转载于:https://www.cnblogs.com/wyboooo/p/10483870.html