递归经典问题----汉诺塔问题
汉诺塔:
问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
这个经典的问题完全可以区分一个人是否学过计算机。
touch here:汉诺塔维基百科地址传送门
他在维基百科上的解释是:The Tower of Hanoi (also called the Tower of Brahma or Lucas’ Tower[1] and sometimes pluralized) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
1.Only one disk can be moved at a time.
2.Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack.
3.No disk may be placed on top of a smaller disk.
如果考虑一下把64片金片,由一根针上移到另一根针上,并且始终保持上小下大的顺序。这需要多少次移动呢?这里需要递归的方法。假设有n片,移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时,
假如每秒钟一次,共需多长时间呢?一个平年365天有31536000 秒,闰年366天有31622400秒,平均每年31556952秒,计算一下:
18446744073709551615秒
这表明移完这些金片需要5845.54亿年以上,而地球存在至今不过45亿年,太阳系的预期寿命据说也就是数百亿年。
如果直接考虑挪动64个盘子有点困难,那么最好的方法是先从一个盘子下手:
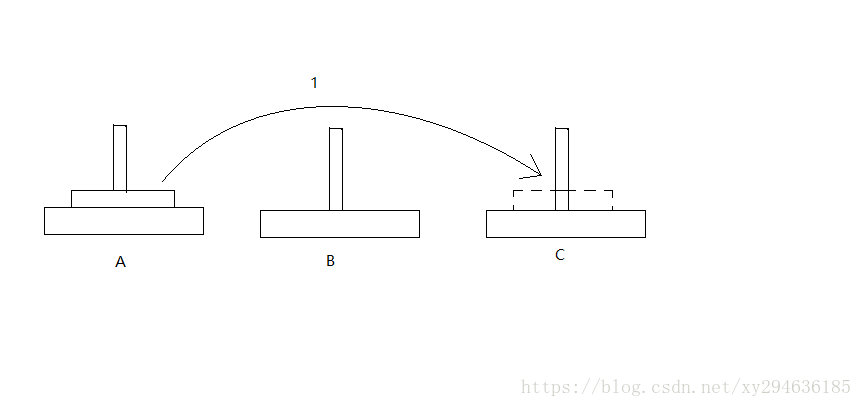
很显然,挪动一个盘子只需要一步。
2.挪动二个盘子
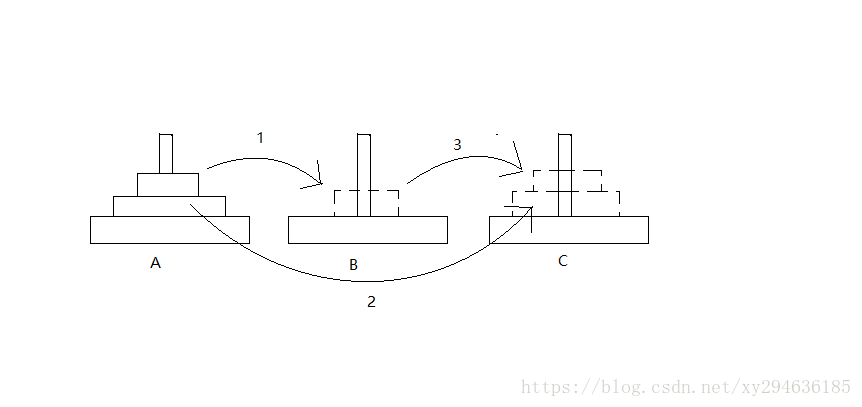
这里需要注意,挪动三个盘子的时候,你会发现当你挪完第一步的时候,也就是把两个盘子转移到第二根柱子时,就变成了和两个盘子一样的状态。所以只需要重复第二步。
这里写成程序就是:
要实现 move(3,A,B,C)
需进行 move(2,A,C,B)
move3 from A to B
move(2,B,A,C)4.挪动4个盘子
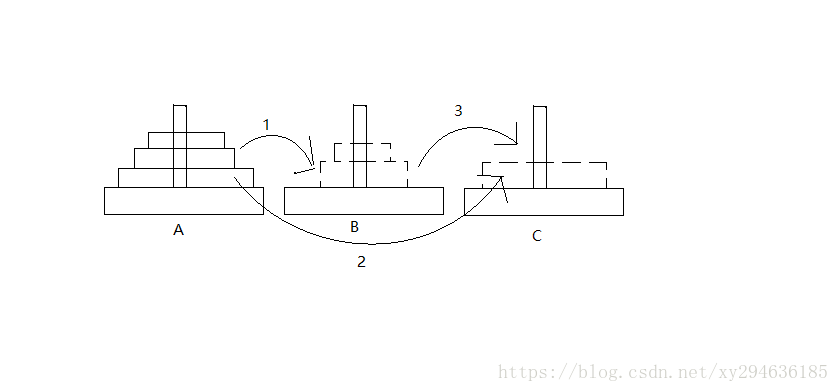
同理,可以简化为挪动三个盘子,继而简化为挪动二个盘子
。
。
。
5.挪动n个盘子
可简化为挪动n-1个盘子。。。到挪动一个盘子。
程序原理如下:
move(n,A,B,C)
move(n-1,A,C,B)
move from A to B
move(n-1,B,A,C)到这里就完成了理论上的研究,接下来就是程序实现了:
#include总结:
利用递归可模拟连续发生的动作。
方法:
1.连续发生的动作是什么:void move(int m, char x,char y,char z)
2.不同次动作之间的关系:move(n-1,x,z,y)
3.边界条件是什么:m==1;