回溯法解决N皇后问题-Python实现（全排列+剪枝）

同系列算法问题

贪心算法解决活动安排-Python实现（排序+贪心选择）

---

N皇后问题

问题

问题概述

分析问题

解决问题

编程

编程流程以及数据类型选择

发现问题以及解决

最终实现

总结

程序缺陷以及完善

解题心路历程

---

问题

在n*n格的棋盘撒上放置彼此不受攻击的n个皇后。按照国际象棋的规矩，皇后可以攻击与之处在同一行或者同一列或者同一斜线上的棋子。N皇后问题等价于在n * n格的棋盘上放置n个皇后，任何2个皇后不放在同一行同一列同一斜线上。

---

问题概述

可以将n*n的棋盘看成一个n*n的表格，放置皇后Q，且需要满足两个条件

• 条件1：同行同列不能放置两个或大于两个皇后
• 条件2：皇后的斜线上不能存在皇后

1	2	...	n
2
...
n

 

例如：

• 4皇后的2种摆法（一种颜色表示一种摆法）：

N皇后也是类似的处理方式

---

分析问题

通过以上的问题概述，可以知道。N皇后的摆法可以通过列表进行将问题抽离出来

例如4皇后问题:

可以定义一个列表嵌套子列表，第i个子列表中表示第i种摆法，那么第1个子列表，即第1种摆法，应该为[1,1,1,1]

不考虑限制条件：

那么问题模型就是[[1,1,1,1],...]，即代表子列表[_,_,_,_]有多少种存放可能，列表又存放子列表，那么4皇后的列表长度为4*4*4*4=256

N皇后的列表长度为n*n*n*n；

首先条件有2个，即上面的条件1和条件2

如何不考虑限制条件的可能再加上这两个条件的限制，那么就是答案了

考虑限制条件-条件1

首先考虑条件1：同行同列不能放置两个或大于两个皇后

子列表表示的是皇后的摆放位置，例如[1,2,3,4]：

那么列表的第1个元素表示的是皇后摆放在棋盘的第一行第一列，

第2个元素表示的是皇后摆放在棋盘的第二行第二列，依次类推

逆推导：行值是列表的第几个元素，列值是列表元素的值

那么，可以知道，当列表中出现两个或者两个以上的相同元素时，即不满足条件1

为了提高算法效率，我们可以将不考虑限制条件和考虑条件1相结合，那么就是全排列算法

例如对于列表[1,2,3,4]，全排列为[1,2,3,4],[1,2,4,3]...一共有4!=24种

考虑限制条件-条件2

条件2：皇后的斜线上不能存在皇后

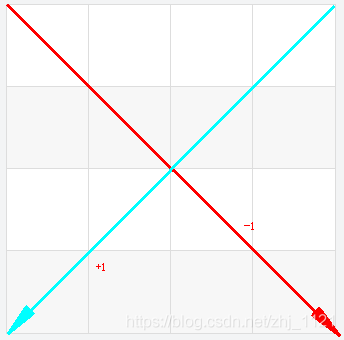
斜线在表格中表示的是斜率为+1的直线，例如以下：

满足条件2，可以将满足条件1问题的所有解空间，进行条件限制，可以通过函数实现，这个函数即是剪枝函数

对于满足条件1问题的所有解空间，模型是[_,_,_,_]

元素的位置是行值,元素的值是列值，例如[1,2,3,4],，即如下表示

从以上模型可得，

i,j表示行值，a[i],a[j]表示列值

• |a[i]-a[j]| = |i-j|，即不满足条件2
• |a[i]-a[j]| != |i-j|,即满足条件2

---

解决问题

• 全排列算法的实现

使用递归和回溯，注意递归体前后语句的意义

• 剪枝函数的实现

函数范围

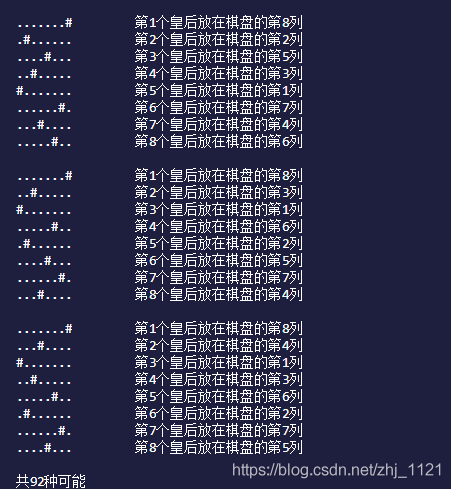
0

i+1

函数逻辑

通过两层for循环实现，通过定义常量，并在语句块中自增，判断语句块是否被执行，实现对解空间的筛选

---

编程

---

编程流程以及数据类型选择

结合以上分析，有以下步骤：

• 首先定义一个列表，为素材列表[1,2,3,..,n]
• 定义一个列表，存储全排列的结果；对素材列表进行全排列，并存入该列表中，为全排列列表
• 定义一个列表，用于存储满足条件2的列表，为结果列表
• 根据结果列表，进行格式打印

---

发现问题以及解决

全排列算法的实现，可以通过问题抽象小化，检查逻辑是否正确。

---

最终实现

程序代码：

#name:queens
#author:zhj1121
#time:2019.11.16
#全排列函数
per_result = []
def per(lst,s,e):
    if s == e:
        per_result.append(list(lst))
    else:
        for i in range(s,e):
            lst[i],lst[s] = lst[s],lst[i]#试探
            per(lst,s+1,e)#递归
            lst[i],lst[s] = lst[s],lst[i]#回溯
#剪枝函数
#args:[1,2,3,4]
#return true or false
def shear(lst):
    result = 0
    for i in range(len(lst)):
        for j in range(i+1,len(lst)):
            if(abs(lst[j] - lst[i]) == abs(j-i)):
                result += 1
    if(result > 0):
        return True
    else:
        return False
#格式打印函数
def stamp(st):
    for i in st:
        for j in range(len(i)):
            a = ("."*(i[j]-1)+"#"+"."*(len(i)-i[j]))
            print(a,"\t","第{}个皇后放在棋盘的第{}列".format(j+1,i[j]))
        print(" ")#负责空行
num = eval(input("请输入皇后的个数："))
lst = [i+1 for i in range(num)]
per(lst,0,num)
queen_lst = []
for i in per_result:
    if(shear(i) == False):
        queen_lst.append(i)
stamp(queen_lst)
print("共{:d}种可能".format(len(queen_lst)))

运行结果截图：

4皇后

8皇后

---

总结

---

程序缺陷以及完善

回溯法解决N皇后问题并不是一个好的算法，之所以这么说，是因为回溯法的使用，类似于穷举法，再加剪枝函数，虽然运行的最终结果是正确的，但其时间复杂度并没有质的改变。

在往后的学习中，会进行尝试使用其它的方式解决问题。

---

解题心路历程

大致如上，不再概述。

---

本篇已完成，如有更改，会在此列出